二阶线性微分方程组解法研究

吴幼明， 冯宝仪

（佛山科学技术学院数学系，广东佛山 528000）

二阶线性微分方程组解法研究

吴幼明， 冯宝仪

（佛山科学技术学院数学系，广东佛山 528000）

采用降阶法和欧拉方法对一类二阶线性微分方程组的求解进行了研究，并给出了当系数矩阵的特征根为三种不同情况（互异、共轭、二重根）时微分方程组的通解公式，并通过算例验证了通解的正确性.

矩阵；微分方程组；线性无关；通解

很多工程技术问题的数学模型都是以微分方程组［1，2］的形式出现，所以对微分方程组的求解问题研究具有现实意义.

针对常系数微分方程组的解法研究，已有很多学者做了深入细致的工作，并得到很多有用的结论.但大部分的工作都是针对一阶微分方程组的研究，如文献［3，4］分别采用初等变换解法和消去法对一阶微分方程组进行了求解；文献［5，6，7］分别采用了递推公式法，矩阵解法和初等解法对一阶微分方程组的解法做了探讨，并得到了通解公式；文献［8］采用标准基解矩阵方法得到了复常系数一阶微分方程组的通解公式，等等.而对高阶微分方程组的研究文献却甚少，文献［9］采用欧拉方法给出了一类二阶微分方程组的通解公式，但该通解公式只适用于系数矩阵的6个特征根互异的情形.本文在文献［9］的基础上详细讨论了当系数矩阵的特征根为三种不同情况（互异、共轭、二重根）时的一类二阶常系数齐次线性微分方程组的通解，并通过算例验证了通解的正确性.本文的结论是文献［9］的延续，因此更具有一般性，为高阶微分方程组的研究提供了重要的参考资料.为了叙述的方便引入一些记号如下：

1 方程组的通解

对式（3）作变换f′1＝f3，f′2＝f4后，整理得

1.1 特征根为互异实根.

若式（6）解得的两根不相等，则矩阵D的特征方程有四个互不相等的根.

当λ＝λ1时，解特征方程（D-λ1E4）ξ＝0，求出特征根λ1对应的特征向量ξ1，即

1.2 特征根为共轭复根.

此时易验证得g1，g2是方程组（3）的解，且g1，g2线性无关.这就得到方程组（3）的两个基解.

1.3 特征根为二重根.

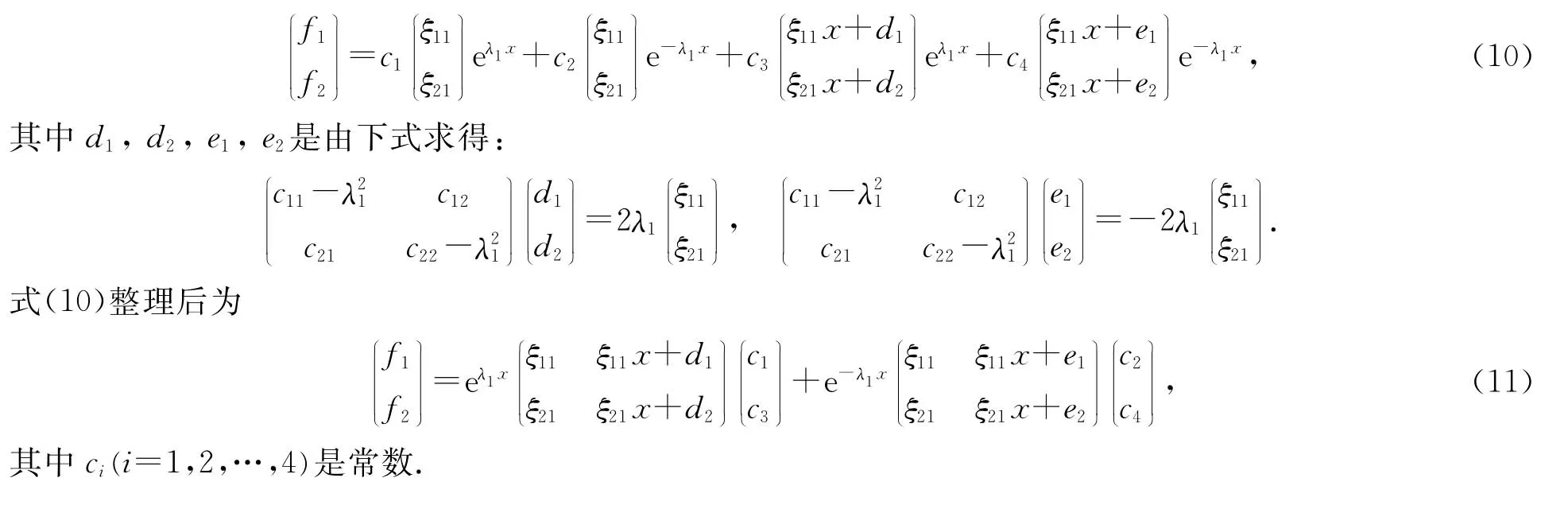
2 算 例

2.1 特征根互异的情形.

2.2 特征根共轭的情形.

2.3 特征根两根相等的情形.

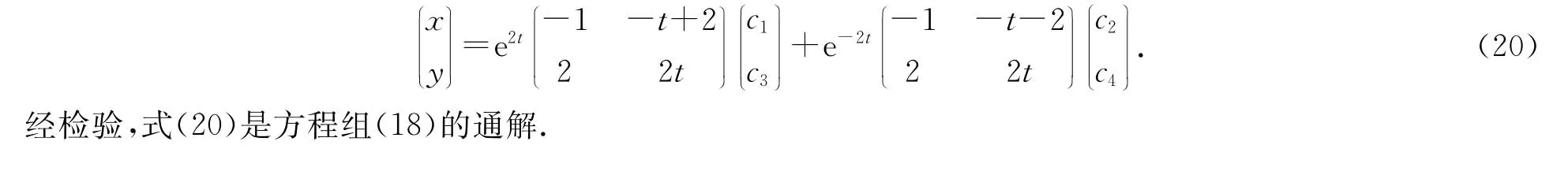
3 结束语

本文利用降阶法和欧拉方法，直接导出一类两个未知函数的二阶常系数线性齐次微分方程组的通解公式，该方法初等、实用.利用本文思想可推出三个及以上的未知函数的二阶常系数线性齐次微分方程组的通解公式.

［1］ 吴幼明，罗旗帜，岳珠峰.考虑多参数分析薄壁箱梁剪滞效应的力学模型［J］.汕头大学学报（自然科学版），2004，19（3）：27-32.

［2］ 吴幼明，罗旗帜，岳珠峰，熊稚军.多因素分析薄壁曲线箱梁剪滞效应的力学模型［J］.中南公路工程，2007，32（3）：42-45.

［3］ 宋燕.常系数齐次线性微分方程组的初等变换解法［J］.辽宁师范大学学报（自然科学版），1995，18（1）：76-81.

［4］ 汤光宋.对用消去法解常系数线性微分方程组的注记［J］.抚州师专学报，1994，（3）：17-21.

［5］ 戴中林.常系数线性齐次微分方程组的递推公式解法［J］.四川师范学院学报（自然科学版），1995，16（2）：158-160.

［6］ 曹玉平.一阶线性常系数微分方程组的矩阵解法［J］.河北理工学院学报，2004，26（1）：104-107.

［7］ 唐烁.常系数线性非齐次微分方程组的初等解法［J］.安徽教育学院学报，2005，23（6）：15-17.

［8］ 邓四清.复常系数线性齐次微分方程组的解法［J］.郴州师专学报（综合版），1997，（3）：22-25.

［9］ 吴幼明，罗旗帜.一类二阶常系数微分方程组的通解［J］.佛山科学技术学院学报（自然科学版），2002，20（2）：10-14.

Research the Solution of the Second Order Linear Differential Equations

WU You-ming， FENG Bao-yi
（Department of Mathematics，Foshan University，Foshan 528000，China）

Research the solution on one kind of the second order linear differential equations by the methods of reducing order and Euler’s eigenvalues.The general solution formulas of the differential equations are obtained when the characteristic root of coefficient matrix is different，conjugate or duplicate.Through some examples，the general solution formulas are validated.

matrix；differential equations；linear independence；general solution

O241.8

C

1672-1454（2011）04-0171-05

2008-09-16

国家自然科学基金资助项目（11026205）