浅析“球体积公式”展示的中外数学思想的异同

曹 媛

浅析“球体积公式”展示的中外数学思想的异同

曹 媛

(天津海运职业学院,天津市 300457)

文本主要探讨刘徽与祖暅对球体积公式的研究以及阿基米德对球体积公式的研究,揭示古代希腊和中国这两个不同数学体系的特征,并就这种差异与各自文化传统之间的关系作一比较。

球体积公式;牟合方盖;平衡法;穷竭法

球体积公式的求解是与微积分早期发展史相联系的一个问题,古希腊和古中国都对这个问题进行了研究并取得了近乎完美的结果,他们方法各异但实质相同,是了解人类早期微积分思想的绝好的案例。三国时期,魏国人刘徽对《九章算术》进行了详细的研究,通过注释对其中的重要数学概念给出定义,对其中的数学方法、计算公式及有关定理都给出符合形式逻辑的论述、推导和证明。球体积公式的研究就是其中的一项。而祖暅原理也是我国传统数学的一个重要的成就,它与兆示着微积分萌芽的卡瓦列里(B.Cavalieri,1598—1647)定理媲美。古希腊阿基米德一生致力于对各种不规则的图形的体积的研究,其中球体积公式的得出是令他最满意的一个。以下是笔者对刘祖和阿基米德数学思想的异同的浅析。

一、刘徽和祖暅对球体积公式的研究体现了构建数学模型的思想

(一)刘徽构造了“牟合方盖”模型

在《九章算术·少广》24题“开立圆术”也给出由计算其直径d的公式

刘徽在为《九章算术》作注的时候,发现“开立圆术”中所给的球体积是错误的,他就想找到推算球体积的方法.在圆柱内切于立方体、球内切于圆柱体、圆内切于正方形时,如果认为

但由于(3)式于理不通,所以(1)式也是不对的。因为古人取3为圆周率,得立方体内接圆柱体为立方体体积的 ,又估计圆柱内接球体积为圆柱体积的 ,故为 .由于错误假设(3)而导出一系列的错误理论,所以牟合方盖的发明即产生于这批判的背景。[1]什么是“牟合方盖”呢?《九章算术》开立圆术中注:取立方棋八枚,皆令立方一寸,积之为立方二寸.规之为圆囷,径二寸,高二寸.又复横规之,则其形有似牟合方盖矣.八棋皆似阳马,圆然也.按合盖者,方率也;丸居其中,即圆率也.推此言之,谓夫圆囷为方率,岂不阙哉?用现代的数学语言解释:牟合方盖就是取棱长一寸的正方体模型八枚,拼成棱长为二寸的正方体.然后由横、纵两个方向各作内切圆柱,两圆柱体公共部分(如图1).“牟”:相等的意思;“盖”:即伞;“牟合方盖”:外表状似上下对称的正方形的伞。[2]

图1

刘徽当时就已经具有了截面定积的思想,即:同高的两个立体,在等高处各作一个与底平行的截面,若截面面积之比为一常数,则此二立体体积之比也等于这一常数.所以对于牟合方盖,如果用同一水平面去截它,就得到一个圆(球的截面),和它的外切正方形(牟合方盖的截面).刘徽指出,在每一高度上的水平截面圆与其外切正方形的面积之比都等于,因此球体积与牟合方盖体积之比也应该等于。

(二)祖暅继承了刘徽的思路创建“祖暅原理”

南北朝时期的祖暅继承了刘徽的思路,但他巧妙地把眼光转向立方体切除“牟合方盖”之后的那部分体积.取牟合方盖的八分之一,考虑它与其外切正方体所围成的立体,并如图2那样把它分成三个小立体,同时考虑一个以外切正方体底面为底,以该正方体一边为垂直棱的倒立方锥.祖暅推证:倒立方锥Ⅴ的体积等于三个小立体的体积之和,因此也等于从外切正方体中挖去牟合方盖的部分,[3]即立体Ⅰ的体积。即 Ⅴ=Ⅱ+Ⅲ+Ⅳ=Ⅰ (4)

图2

对于(4)式的证明,祖暅是这样做的:考察在高h处的水平截面(如图3),容易看出三个小立体Ⅱ、Ⅲ、Ⅳ的截面(阴影部分)的面积ASQP,CTQR与BSQT合并在一起应等于正方体截面积ABCD与牟合方盖部分的截面积PQRD之差,即

ASQP+CTQR+BSQT=ABCD-PQRD

设 AS=PQ=x,则有 ABCD-PQRD=r2-x2,由勾股定理可知,r2-x2=h2,故 ASQP+CTQR+BSQT=h2,根据刘徽截面定积的思想,在高h处的倒立方锥V的截面积也等于 h2.(因为截面的边长为h,并且截面是正方形)这就是说,在任意等高处,立体Ⅰ的截面积与倒立方锥的截面积相等,因而,它们的体积相等.而倒立方锥的体积刘徽已解决了,等于(r为小正方体的边长,即球半径).这样整个牟合方盖的体积就是.再由刘徽先前所得的结果 V可推得

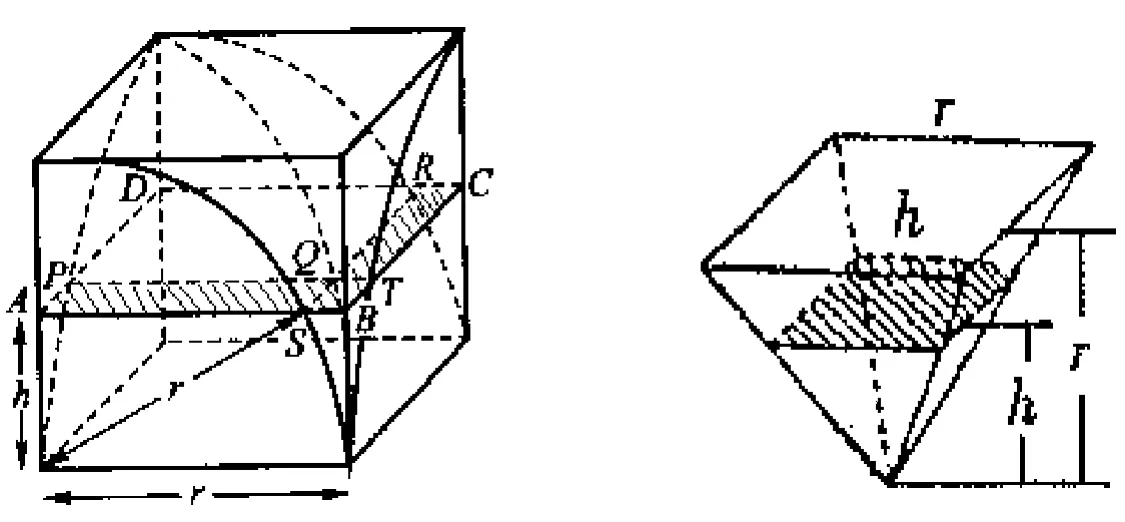
图3

二、阿基米德对球体积公式的研究展示了“平衡法”的思想

阿基米德(前287-212)是亚历山大时期最伟大的一位数学家。他的数学研究包括用穷竭法求面积和体积,计算 ,并提出用语言表示过剩近似值的一种新方案。在力学方面,他算出许多平面形和立体形的中心并给出杠杆原理.他奠定了论述水中浮体平衡问题的流体静力学的基础.[4]在天文学方面,他制作过一台行星仪,可惜关于天文学的著作失传了,他的光学著作《镜面反射》,没有保存下来.[5]阿基米德用两种方法来推导球体积公式。在《论球与圆柱》卷中,他以33个命题准备,然后用反证法在命题34得到结论:球体积等于以球的大圆为底,球半径为高的圆锥体积的四倍.在另一著作《方法》中,他再次讨论球体积公式,取法简便,用力学的方法得到同样的结果.有趣的是,阿基米德也曾研究过牟合方盖。[7]

在《方法》中阿基米德用一种称为“平衡法”的方法来推算球体积的公式.实质上是一种原始的积分方法。在以O为圆心,以r为半径的圆中(如图4),作两条互相垂直的直径AB和 CD.连结AC并延长使之与过B且垂直于AB的直线相交于 E,连结AD并延长到与 EB交于F.我们看到 EB=2 r=B F,这是因为角BAE和BAF各为45°.这样就构成了一个以 EF为底,以AB为高的矩形EFGH.PQ是过AB上的一个任意点X所作的一条垂直于AB的直线,它与圆相交于 R和S,与AE交于 T,与AF交于U.我们设 X T=x,XR=y,还有 A X=x,从直角三角形AXR中,可以看出

图4

从直角三角形ARB(点R上的角为直角,因为它与直径相对)中,我们得到

这是因为直角三角形的一条直角边是它在斜边上的投影和整条斜边的比例中项.联立(5)、(6)式,我们有

将AB向A外延长到W,使得WA=2r.作图到此结束。

现在我们把整个图形绕AB旋转,那么该圆就生成一个半径为的球;三角形 EAF生成一圆锥,此圆锥的底是半径为B E=2 r的圆,高是 AB=2 r;而矩形 EFGH生成一圆柱,其底半径为 B E=2 r,高为AB=2 r.在旋转过程中,任一直线PQ扫过一平面,它截该圆柱于半径为2r的圆;截圆锥于半径为x的圆C1;截球于半径为截球于半径为y的圆C2.

用(2r)2除(7)式的两边,可知

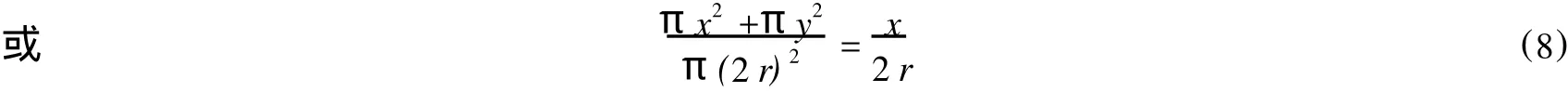
现在把WB当作支在A点的杠杆,而方程(8)可用下述方法解释为杠杆的平衡条件:圆C1和C2(分别从圆锥和球中割出)面积之和与半径为2r的圆(从圆柱中割出)的面积之比等于从A到X的距离与从A到W的距离2r之比.换句话说,如果我们想象圆片的重量与其面积成正比,那么对以A为支点的杠杆来说,在W点悬挂圆C1和C2将与X点悬挂面积为π(2 r)2的圆平衡。

这一平衡条件对于在 HG和EF之间任一位置的PQ都是满足的.如果我们把圆柱、球和圆锥看成是由PQ扫过的每一个可能平面从实心体中所切出的圆构成,并且对每个PQ,都把C1和C2悬挂于W,那么所有的圆重新组成圆锥和球,并将与圆柱平衡.由于圆柱体的重心位于圆O,故我们可把这表示为:或或2(球+圆锥 EA F)=圆柱。由于圆柱是圆锥的3倍,我们得到2·球=圆锥 EA F.但圆锥 EA F=8圆锥 CA。由于当一图形的线形尺度乘以时,其体积得乘以,因此球=4圆锥.或者说一个球等于以球的大圆为底,以球半径为高的圆锥的四倍。[6]

由此可见,这种“平衡法”是阿基米德发现数学真理的主要方法之一,其要点是,体积是由面积构成的,面积是由彼此平行的直线构成的,每条直线都有重量,而且与它们的长度成正比,因而可以把问题归结于使未知的几何图形与已知的几何图形相互平衡以及求出重心.[5]但是,在阿基米德爱挑剔的眼光里,使他认为力学方法不能用作证明的原因在于把实心物体看作是平面截面之和。现今我们对于“积分”的方法已经很熟悉了,但阿基米德却成功的把积分的困难转移到了确定圆柱体的重心上,而后者是十分简单的事情,只要考虑对称性就可以了。[6]

三、刘、祖与阿基米德关于球体积公式研究的异同多角度体现了数学文化的魅力

(一)“构建数学模型”是中外数学家思想的相同之处

所谓数学直觉,是指在数学活动中,数学经验作用于人的感觉器官而在大脑中产生的感觉、知觉、表象等反映,是人脑对数学对象的一种迅速而直接的洞察和领悟,它是人类生活中普遍存在的直觉现象在数学创造活动中的表现,数学直觉思维的培养直接影响着创造能力的提高。

在球体积的问题上,刘徽想到构造一个图形——牟合方盖,而后再通过截面定积的思想得出 。并且他还注意到,不管是球内切、外接于立方,或是立方内接、外切于球,只要几何关系不变,则二浑或二质比例关系不变,这反映了他注重通过特定条件研究不变比例关系的数学观点。[1]刘徽的积分思想包含了以下几层含义:刘徽极限的观念与割圆术联系紧密,并且是他对割补法、分割法深入研究的结果;刘徽“不失本率”原理的进一步发展,为了“不失本率”,必须“所失弥少”,因而在做法上必须“割之弥细”;刘徽对“化曲为直”和“化直为曲”这种朴素思想方法进行精确考究的结果.他以圆内接正多边形的面积逼近圆面积,要做到“与圆合体而无所失”,显然要“割之又割,以至于不可割”;刘徽把“无限可分”“,无限变化”“,存在极限”等观念,在理论上、方法上加以整理,并把它拿到数学领域中加以运用了扩充.他把极限观念与数学运算结合起来进行考察,因而为中国古代数学理论研究开辟了一条新的路径,即把极限思想也作为重要的数学理论基础。[10]但唯一的遗憾是他没有得到牟合方盖的体积,因此并没有求出球体积的公式。但是刘徽构造出的牟合方盖从理论上提出了推算球体积的正确途径,祖暅则在此基础上正确推导出球体积公式。

阿基米德也曾研究过这一立体,在阿基米德的《方法》前言中说他新发现两个立体体积公式,其中一个就是刘徽称为牟合方盖的立体。“一圆柱内切于立方体,其上下底在立方体两相对面内,侧面则切于另外四面,在同一立方体内,又内切另一圆柱体,以另外两相对面为上下底,圆柱体侧面切于其余四面,这两个圆柱体公共部分的体积是立方体体积的三分之二。”[7]阿基米德的数学积分思想主要体现在平衡法和穷竭法上,由于阿基米德本身是个物理学家,所以他更擅长用物理的定义去构建数学模型。他利用力学原理,也就是杠杆原理求出了不规则图形的面积,再由面积扩展为体积,借助于这种数学模型大胆尝试,最后应用“穷竭法”的数学思想将体积公式完美论证。

(二)中外数学家不同的生活背景、历史环境影响了他们数学思想的形成

中国古代数学家关心的主要是得到实用的结果。并且古中国哲学不排斥归纳、类比和经验手段,这就给科学理论带来了直观和思辩的特点。刘徽利用“出入相补”的原理来解决平面几何的有关问题,是我国古代数学的传统特色。刘徽成功地应用“出入相补”的原理和“有限割补”法,以长方形面积法为基础,建立一系列平面直线形的求积理论。并以此为基础,把他所要研究的直线形,运用“出入相补”的原理,把它分割成为与之等积的长方形,然后按照长方形求面积的算法来推算其他图形的面积。若是复杂的直线形,则是先化为若干基本直线形,再化为长方形。同样由长方形的求积算法推证之。对于曲线形面积,刘徽用极限思想采用“割圆术”证明圆面积公式,然后以圆面积理论为基础再作推算。在“割圆术”中刘徽认为圆内接正多边形,“割之弥细,所失弥少。割之又割,以至于不可割,则与圆合体,而无所失矣。”这是很明确的极限思想。而对于立体图形体积算法的推导,刘徽以体积概念和长方体体积算法为基本单位,同样根据“出入相补”原理进行推导。但是,“出入相补”原理较适用于简单几何图形,对于较复杂的图形(曲边形)求积,就显得有局限性了。因为“出入相补”局限于有限次的分割,而对于曲边图形,通过有限分割是达不到对其精确求积的。[9]所以刘徽没有得到球体积的公式,而祖暅在刘徽“出入相补”原理的基础上,运用了“体积之比等于对应截面面积之比”的思想,成功的推算出球体积的公式。而祖暅提出来的思想,相当于17世纪意大利学者卡瓦列里提出的“卡瓦列里原理”:如果两个立体图形夹在两个平行平面之间,并且为任何平行于这两个平行平面的平面所截得平面片的面积都相等,那么这两个立体图形的体积相等;如果截得两个立体所得的两组截面中,每个给定平面所截得的两个不同组的截面面积都有相同的比例,则这两个立体的体积也成相同的比。[9]

古希腊是崇尚哲学的,所以数学的发展就受到了两个因素的制约:一是演绎推理被赋予唯一合法的地位,二是数学被视为建立统一的宇宙图景的工具。由于前者的刺激,形式逻辑和几何学得到充分发展,后者则不容忍数学出现任何可笑的纰漏,否则就可能导致全部哲学信念的崩溃。阿基米德对球体积公式求解过程中,主要应用了“平衡法”,他认为立体是由面积元素构成的。而“平衡法”在数学上就是认为图形是由许多微小量组成的,立体图形是由许多彼此平行的截面组成的。把含有未知量的图形分解为组成它们的微小量,然后再用另一种微小量来与它们比较,比较时利用力学的原理,赋予所有微小量以理想的重量,于是几何图形就可以看作是具有理想重量的重物,再建立一个杠杆,找到合适的支点,使前后两组微小量的总体,通过比较求出各未知量来。因此,平衡法体现了近代积分法的基本思想。当然,阿基米德意识到平衡法严密性上的不足,所以当他用平衡法求出一个面积或体积后,必再用穷竭法给以严格的证明。这种发现与求证的双重方法,是阿基米德独特的思维方式,这也是他不同于中国两位数学家思维的地方。[8]

[1]罗见今.关于刘祖原理的对话[M].刘徽研究.西安:陕西人民教育出版社 ,1993.

[2]高红成,王瑞.祖暅原理的形成及其现实教育意义[J].商洛师范专科学校学报,(04).

[3]李文林.数学史与数学教育[M].汉字文化圈数学传统与数学教育.北京:科学出版社,2004.

[4]M.克莱因.古今数学思想第一册[M].上海:上海科学技术出版社,2002.

[5]中外数学简史编写组.外国数学简史[M].济南:山东教育出版社,1987.

[6]A.艾鲍著.周民强译.早期数学史选编[M].北京:北京大学出版社,1990.

[7]吴文俊.中国数学史大系[M].北京:北京师范大学出版社,1999.

[8]刘钝.阿基米德、刘徽关于圆的研究之比较[J].自然辩证法通讯,1985,(07):51-56.

[9]梁宗巨.世界数学通史(下册)[M].沈阳:辽宁教育出版社,2005.

[10]郭金斌,徐梦秋.中国传统数学思想史[M].北京:科学出版社,2005.

The Comparison Between Chinese and Foreign Mathematics Thinking by Demonstrating the Formula of Sp here Volume

CAO Yuan

(Tianjin Maritime Vocational Institute,Tianjin 300457 China)

The article mainly explores the different researches on the f ormula of sp here volume by Liu Hui,Zu Geng and Archimedes,reveals the different characteristics of Chinese mathematics system and that of Ancient Greece and compares the relationships between the differences and their cultural tra2 ditions.

f ormula of sphere volume;balanced law;method of exhaustion

G712

A

1673-582X(2011)06-0092-06

2010-06-17

曹媛(1983-),女,天津市人,天津海运职业学院基础课部助教,主要从事高职数学工作。