斜纹过滤布的经纬纱密度对其孔径的影响

闫 哲 论， 李 淳， 杨 丽 芳

（1.大连工业大学 纺织轻工学院，辽宁 大连 116034；2.辽宁天维纺织研究建筑设计有限公司，辽宁 沈阳 110016）

0 引 言

过滤介质是一种用于过滤的具有较大内表面和适当孔隙的物质，它能有效地捕获和吸附固体颗粒或液体粒子，使之从混合物质中分离出来［1］。机织过滤布是过滤介质的一种。孔径是机织过滤布生产和使用的重要指标。织物的孔径由纱线之间形成的通道和纱线间纤维的空隙组成，这种孔径并非真实的圆形孔径，是一种等效孔径。现阶段，对于多孔材料孔径的测量技术主要有气泡检测法、汞压入法、透过法、中流量孔径法［2］。现有气泡法孔径测试方法的缺点在于在测量时需要操作人员记录气泡冒出试样瞬间的气体压力，并以此瞬间的压力值为测量值，即最大孔径。由于操作困难，误差不可避免。另外以一种沸腾现象时的压力值作为沸腾孔径，而“沸腾”现象不能被定量地描述，每个人对“沸腾”现象的判断都是不一样的，所以必然会产生人为误差。前人对机织滤布的冒泡法测试的孔径进行的研究中，分析了影响机织过滤布孔径的主要因素［3］。研究认为滤布的紧度对最大冒泡孔径有显著影响［4］。已有文献很少有定量分析经纬密对孔径的影响。本文采用一种新型的冒泡孔径测量装置测量过滤布的孔径，可以有效降低人为原因产生的测量误差。针对一种市场上常用过滤布，将其经纬密有序变化，定量地研究过滤布的经纬纱密度变化对其孔径影响，以期对过滤布的设计和选型有所帮助。

1 实 验

1.1 试 样

以市场上一种常用的机织滤布（大连华隆滤布有限公司提供）为基础，变化其经纬纱密度。过滤布的工艺参数：组织，3／3 斜纹；经纱线密度，300D×7；纬纱线密度，300 D×4；经纱捻度，171T／m；纬纱捻度60T／m。经纬纱均涤纶复丝。

把经密分别设定为353、333、313、293、273、253根／dm 时，纬密设定为122根／dm；当纬密设定为130、122、114、106、98、90根／dm 时，经密则设定为273根／dm。这样设计经密和纬密的原因是，过滤布不仅要满足过滤的性能要求而且要承受过滤时产生的压力，所以织造过滤布的纱线较粗，这样也使得织造工艺有极限要求。为了满足过滤布的强度和织造工艺的要求，设计了以上实用的变化区间。

1.2 实验原理

实验仪器液体压强是根据随着液体深度的增加液体压强在增加的原理设计的。将被测布样与地平面垂直放置，布样受到液体的压强随着液体深度的增加而增加，这样就使得试样孔隙中的压力差随着深度的增加而减小。假设试样的空隙是均匀一致的，气泡冒出试样表面所需要的压力差为Δp，试样孔隙中压力差大于Δp 的位置有气泡冒出，而压力小于Δp 的位置没有气泡冒出。点a表示压力差为Δp 的位置，也就是说点a 位置上方全部的试样表面都有气泡冒出，而下方没有气泡，点a位置是测量点。通过调节气体压力可以使测量点a 在试样表面上下移动。但实际情况下，被测量的过滤布的孔径不是均匀的，在测量点a以下会有零星的大于点a 孔径的孔隙冒出气泡。这一现象用理论曲线可以表示为图1所示，在一定的气体压力下液面高度h与气泡数n 的关系，也就是说深度越深气泡数量越少，拐点a即所要求的测量点。

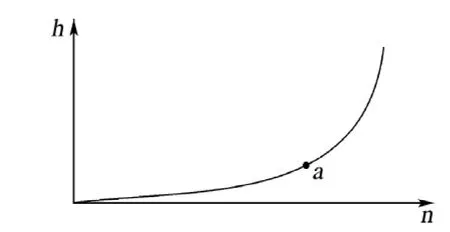
图1 液体深度（h）与冒泡数量（n）的关系Fig.1 Relationship between liquid height（h）and bubble number（n）

实验装置产生的气液压力差

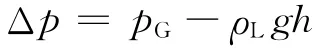
根据公式［5］Δp=4γcosθ／D 得计算公式：

式中，Δp 为压力差，pG为气体压 力，ρL 为液体密度，g 为重力加速度，h为液体深度，γ 为液体表面张力，θ为液体于孔壁的接触角，D 为孔的直径。

在过滤布样品从上至下随机取6个点，将这6点的平均值作为孔径值。

1.3 实验装置

如图2所示。将待测滤材3安放在气体箱1与液体箱2中间的待测滤材安放区中，气源由微型空气压缩机12提供，气源进入储气罐13得到稳压后，通过调节旋拧阀11控制进入测量盒的进气量即测量盒中的压力差Δp，多余气体由放气阀14放出。安全阀9、10对压力表起保护作用。通过两块不同量程且不同精度等级的压力表9、10读出测量点的压力差Δp。此压差在液体箱2、气体箱1和待测滤材3中产生，通过观察窗4观察测量点，并用深度刻度尺5记录测量点的液体深度。用温度计15测量试液（异丙醇）的温度。

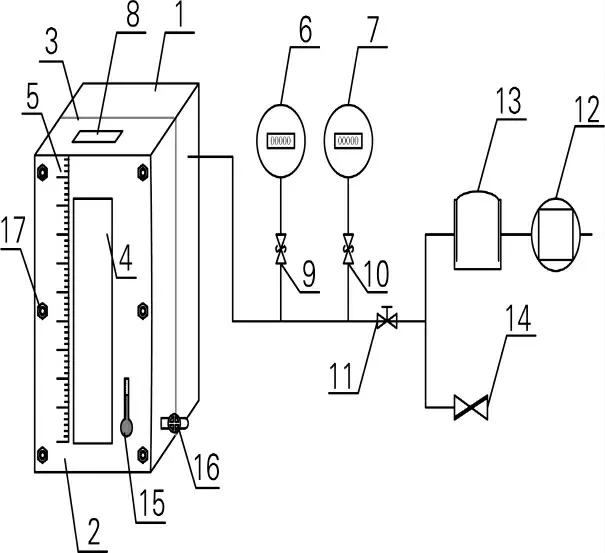
图2 实验装置Fig.2 Experimental instrument

2 结果与讨论

2.1 经密与过滤布孔径的关系

当纬密设定为122 根／dm，经密分别设定为353、333、313、293、273、253 根／dm 时，测 定 滤 布的孔径见图3。由图3可知，过滤布的孔径随着经密的变小而逐渐增大。通过数据分析发现经密的变化和孔径之间存在着某种函数关系。对实验数据进行回归分析，可以得出经密x 与孔径y 之间具有如下关系：

y=1 161.845 3-5.781 6x+0.007 8x2

x ∈［253，353］，相关系数R=0.999 5。

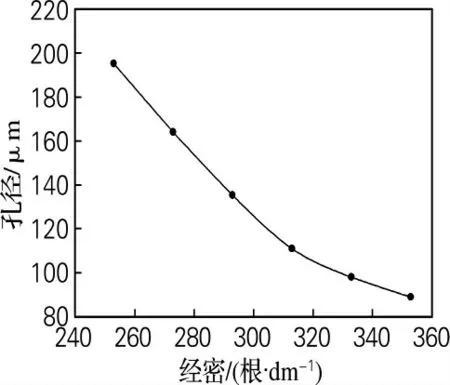
图3 孔径与经密的关系Fig.3 Relationship between pore size and warp density

2.2 纬密与过滤布孔径的关系

当经密定为273 根／dm，纬密分别设定为130、122、114、106、98、90 根／dm 时，测定滤布的孔径见图4。由图4可以看出，过滤布的孔径随着纬密的变小而增加。同样可以得出纬密x 与孔径y 有如下关系：

y=1 374.695 1-17.637 7x+0.063 2x2

x ∈［90，130］，相关系数R=0.999 5。

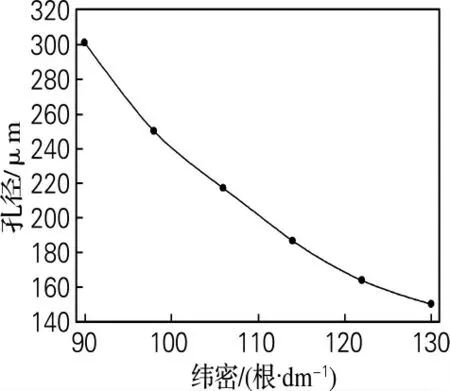
图4 孔径与纬密的关系Fig.4 Relationship between pore size and weft density

2.3 过滤布孔径与经密和纬密的关系

通过经密、纬密对过滤布孔径的讨论可以看出，经密和纬密都在有规律地影响着孔径的变化。孔径y 与经密x1和纬密x2有如下关系：

x1∈［253，353］，x2∈［90，130］，相关系数R=0.999 6。函数关系如图5所示。

通过对影响过滤布孔径的回归方程可以看出，每改变一个单位，经密对孔径的影响小于纬密的影响。当进行特定斜纹过滤布的设计时，可以根据上述结论并结合实际要求和成本预算，得出所要的经密与纬密。

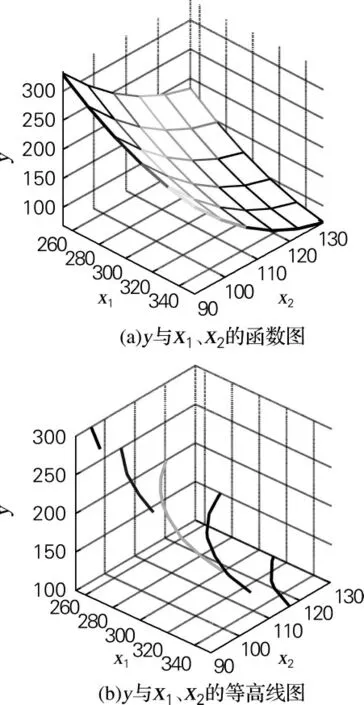
图5 孔径与经密和纬密的关系Fig.5 Relationship of pore size with warp density and weft density

3 结 论

将研究结论与过滤布织造成本相结合，可以以最小成本得到预期孔径的过滤布，使过滤布的设计有理论依据。得到的回归方程只适合于3／3斜纹组织过滤布。因为不同组织、不同纱线的过滤布，其经密、纬密对孔径的影响不同，所以不是任意一种过滤布全都能用本研究的关系描述。后续工作需要将过滤布进行系统化的研究，分别找出其工艺参数与孔径的关系，建立数据库，将对过滤布的设计和应用选型带来更大的帮助。

［1］郁铭芳，孙晋良，邢声远，等.纺织新原料与纺织品应用领域新发展［M］.北京：清华大学出版社，2002：178.

［2］张清，张正德，魏海荣.多孔材料过滤精度表征方法［J］.过滤与分离，2000，10（1）：33-37.

［3］毛成栋，张明光，郭昕.机织滤布鼓泡孔径测试与分析［J］.纺织学报，2008，29（5）：39-41.

［4］张明光，徐新阳，毛成栋.机织过滤布鼓泡孔径的研究［J］.过滤与分离，2002，12（1）：14-15.

［5］PURCHAS D B，SUTHERLAND K.Hand Book of Filter Media［M］.London：Elsevier，2002：463.