阀门产品的可靠性评估方法

崔景芝 修建生 孙法国 丁建春

（北京宇航系统工程研究所）

1 前言

阀门是运载火箭增压输送系统的重要元件，用于实现气体输送、截止、调节、排放、超压保护和推进剂加泄、溢出等功能。作为运载火箭上天后进行动作的精密机械产品，阀门结构、动作原理比较复杂，上天后的工作剖面因遥测参数有限很难准确量化，这些都给阀门飞行性能可靠性验证带来一定的困难。如何提出一套经济可行的试验办法验证阀门性能可靠性尤为关键，针对当前国内外阀门产品可靠性评估现状进行了调研分析，并根据载人航天运载火箭增压输送系统阀门产品的特点，制定了相应的可靠性评估方法。

2 阀门产品可靠性评估国内外研究状况

国内对机械产品的可靠性评估做了大量的研究工作，但是专门针对阀门的可靠性评估的研究很少。当前主要工作如下：文献[1]中，设计了阀门的可靠性试验，并对试验结果进行分析处理，对产品的平均无故障工作寿命（MTBF）、使用寿命和可靠寿命作了一个统计的、定量的评估。文献[2]以CANDU重水堆电站应急堆芯冷却系统电动重水隔离阀为主要研究对象，探索核电站安全相关系统设备可靠性分析与定期试验频率优化的方法，建立一套能够根据设备具体状况评估其可靠性的分析管理体系。

国外对阀门的可靠性评估中，文献[3]研究了阀门可靠性的评估方法，他认为统计学的方法只是以现有的和试验失效数据的基础上进行可靠性评估；而参数法主要在指定工作时期或试验持续时间内有关参数变化的数据的基础上进行评估，参数法与统计学的方法相比，参数法允许减少试验品的件数和试验的持续时间。文献[4]利用参数估计的方法对发动机操作阀进行概率风险评估，估计元件随时间变化的失效率。文献[5]利用Atwood文中部件失效数据运用非参数最大似然估计的方法进行估计，并与Atwood文中的计算结果进行了对比，得到结论认为在参数和非参数的计算模型中对数据不同的处理方法，会给评估结果带来显著不同。文献[6]建立了一种新的评估模型并利用其进行失效率的评估，并且与标准指数模型进行评估结果的比较，得出其优于标准指数模型的结论；但是其建模过程中存在很多假设，所以文中的方法也有一些缺陷。一些关键的可靠性参数的评估结果很大程度上依赖于模型的选取，而不仅仅是观察到的各种故障数据。关于阀门的工作寿命的分布，文献[7]对新设计的泵阀进行试验并和标准的泵阀相比较，结果显示寿命有了提高，他提出阀门的工作寿命服从正态分布或对数正态分布。文献[8]以水面控制的水下安全阀为例提出，将阀门寿命看作其符合Weibull分布，代替我们通常采用的指数分布类型，他主要研究了影响阀门寿命的因素，假设两参数的Weibull分布代替固定的故障率，在研究相关的失效机理的基础上，证明Weibull分布应用在阀门上是正确可行的；并在此基础上，利用随机观察到的数据对MTTF（mean time to failure）和MFDT（mean fractional dead-time）进行评估。文献［8］对阀门的MTTF和MFDT的评估结果随着模型和模型参数选取的变化是不稳定的。通常大部分的风险和可靠性研究都是建立在失效率是常数的基础上，可利用的数据不足以确定一个更真实的寿命分布，并估计出这个分布的参数。因此，经常将其寿命分布默认为指数分布。文献［8］中利用Weibull分布讨论建立了新的模型，为阀门的评估提供了一个新的思路。

3 载人航天阀门产品可靠性评估原则及重要意义

载人航天阀门的可靠性评估是指根据阀门样本数据对阀门可靠性进行统计推断，根据可能收集到的有关试验（包括专门的可靠性试验和其他的工程研制试验）或计算仿真的数据与信息对阀门的可靠性指标做出估计，从而得出阀门对于所要求的可靠性指标的符合程度，其重要意义在于：

（1）通过评估，检验产品是否达到了可靠性要求，并验证可靠性设计的合理性，如可靠性分配的合理性，冗余设计的合理性，选用元器件、原材料及加工工艺的合理性等等。

（2）评估工作会促进可靠性与环境工作的结合。在可靠性评估中，要定量地计算不同环境对可靠性的影响，要验证产品的抗环境设计的合理性，验证改善产品微环境的效果。

（3）通过评估，可以指出产品的薄弱环节，为改进设计和制造工艺指明方向，从而加速产品研制的可靠性增长过程。

（4）通过评估，了解有关元器件、原材料、整机乃至系统的可靠性水平，这为制定新产品的可靠性计划提供了依据。

（5）可靠性评估工作需要进行数据记录、分析及反馈，从而加强了数据网的建设。对于我国机械产品可靠性的研究工作具有重要意义。

4 载人航天箭体阀门的可靠性试验评估方法的选取

针对运载火箭阀门可靠性评估试验周期长、高费用的特点，不可能针对阀门整体做大量的可靠性试验来获取可靠性数据，但是对于各个单元，我们却能做相对大量的试验来获取试验数据。鉴于以上情况为了对阀门的可靠性指标做到相对精确的评估，我们选用金字塔模型，即先对下一级各功能单元进行评估，然后将试验信息向上一级折合，再把折合信息与上一级的试验信息进行综合，进行各级系统可靠性综合评估。

具体的实施方法为：通过建立阀门的功能框图和可靠性框图，并对其进行分析，我们可以将阀门看作一个串联系统。先对组成阀门的各个单元进行评估，再将单元的信息折合到系统进行评估。对单元的评估方法主要有：经典方法、Bayes方法和Fiducial方法，前两种方法比较普遍。但因为Bayes方法需要利用验前分布和当前试验信息，由于我们缺乏以前积累的数据，验前信息的获取和验前分布的表示都无法实现。所以尽管Bayes方法的理论已经相对成熟，我们仍无法用其进行单元评估。在单元评估时，我们利用经典方法进行评估。

对系统评估时，我们采用L－M法和MML法进行系统评估。

5 减压器可靠性评估案例

5.1 减压器各单元的评估

减压器可靠性框图如图1所示：

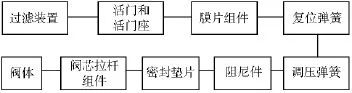
图1 减压器可靠性框图

根据减压器的可靠性框图，减压器所包括：过滤装置、活门和活门座、膜片组件、复位弹簧、调压弹簧、密封垫片、阻尼件和阀芯拉杆、阀体。我们分别对其进行评估。

此处需要说明的是：

（1）根据FMEA及FMECA分析，对于几乎不发生故障的零部件，如过滤装置、复位弹簧和调压弹簧，可视其可靠度为1，不再对其可靠性进行评估。

（2）为了评估阀门所有起密封作用的元件的可靠性，例如减压器各个部位的垫片、活门和活门座等具有密封作用的元件，我们采取对整个阀门作密封试验的方法。将所有元件看作一个统一单元进行评估。

根据以上分析确定减压器所需评估的单元为：密封元件、阀芯拉杆组件、膜片组件、阀体。

5.1.1密封元件

首先对整个阀门作密封试验，设试验时阀门的漏气量为n泡/秒。规定每秒钟阀门的漏气量n≤k时，则阀门正常，否则算作失效。则k为其性能指标的置信上限。

对阀门进行密封试验，设得到的漏气量数据为：x1，x2，…xn，对试验数据进行分布拟合检验，对于单元的性能指标而言，一般服从正态分布。假设得到的分布数据经过拟合优度检验后服从正态分布，我们就可以利用数据对分布函数的均值和标准差进行估计，得到。又知其性能指标的上限值 k，然后利用正态性能型单元的可靠性评估方法进行评估。最后得到所有密封元件的可靠度，及可靠性置信下限。

5.1.2阀芯拉杆组件

根据对减压器的FMEA及FMECA分析，阀芯拉杆组件的主要问题表现为动作不灵敏，甚至会出现抱死的情况，究其原因是由于活门与衬套之间摩擦力过大。但是当二者摩擦力太小时，又不能满足减压器的性能指标要求。

对阀芯拉杆的评估思路为：将活门与衬套之间的摩擦力作为特征量给定一个上限值U及下限值L，然后进行试验测定出一组摩擦力的值x1，x2，…xn，对试验数据进行分布拟合检验，对于单元的性能指标而言，一般服从正态分布。假设得到的分布数据经过拟合优度检验后服从正态分布，然后再利用数据对分布函数的均值和标准差进行估计，得到。然后利用正态性能型单元的可靠性评估方法进行评估。得到阀芯拉杆组件的可靠度及可靠度置信下限。

5.1.3膜片组件

根据对减压器的FMEA及FMECA分析，膜片的重要度最大，且膜片极易出现故障，其故障率的排序处于第三位，在此将阀芯的可靠度定为1，只需要对膜片进行评估。

（1）首先选取大量样本进行完全样本的疲劳试验（如果试验进行到所有参加试验的样本全部故障为止，则称为完全样本试验），可以得到大量的膜片的疲劳寿命数据。

（2）根据所得到得疲劳寿命失效数据 ，采用异常值检验方法和拟合优度检验方法，剔除异常值并且确定单元得寿命分布类型（例如正态分布、对数正态分布、指数分布、Weibull分布等）

（3）最后根据其寿命分布类型，选择与膜片寿命分布类型对应的可靠性评估方法，进行膜片的可靠性评估。假设我们采用异常值检验方法和拟合优度检验方法进行数据检验，确定出其寿命符合Weibull分布，利用Weibull寿命型单元的可靠性评估方法进行评估，得到膜片的可靠度和可靠度置信下限。

5.1.4阀体

对阀体进行评估时，根据对减压器的FMEA及FMECA分析，将螺盖、衬套、限制盘和弹簧壳的可靠度定为1，选取壳体和密封垫片进行试验和评估，前面已经提到，对密封垫片的试验在对密封元件的试验中整体进行，故在此只对壳体进行应力—强度试验。

进行应力强度试验时，做出假设，应力与强度均符合正态分布。

（1）当强度分布参数均值与方差未知，应力取极限值时，利用点估计方法得到可靠性的点估计，及可靠性置信下限。

（2）当强度与应力分布参数均值与方差都未知时，分别作强度试验及应力试验，设强度试验结果取得 nx个强度试验值：x1，x2，…xnx；应力试验结果取得ny个应力试验值：y1，y2，…yny。利用可靠性的点估计得到，及可靠性置信下限。

5.1.5减压器最终评估单元

根据以上分析，减压器最终所评估的单元如下图所示：

图2 减压器最终评估单元

5.2 减压器的系统可靠性评估实例

（1）减压器失效判别标准

减压器失效模式为导向不灵或零件损坏造成控制压力带超标。

（2）可靠性特征量

根据减压器的动作特性可定义其可靠性特征量为满足压力上、下限要求的调节次数。

（3）任务剖面确定

根据火箭飞行贮箱遥测参数，减压器在一次飞行过程中大约开启3～5次，考虑一定的余量，飞行任务剖面定为开启、关闭10次。

（4）分布类型选取

从以上分析可知减压器性能分布选择Weibull分布是可行的。采取Weibull寿命型方法对箭体阀门进行可靠性评估时，规定任务时间一般选定阀门使用时的工作次数或火箭飞行总时间。然后选定合理的试验件数量，根据可靠性指标要求进行定时结尾寿命试验。

（5）试验件、试验时间的确定

设Weibull寿命型（双参数）单机产品的试验数据为（n，r，t1≤…tn），即共投入 n 个样本进行试验，试验中共有r个产品失效，则单机产品可靠性置信下限RL的计算公式为：

式中m为形状参数，是衡量寿命分散性的尺度，一般m取2～3，具体值应根据试验数据估计而得或根据工程经验判定。

然而，由于受到试验件数量的限制（试验件一般为6件），在用公式（1）进行评估时，只要一件失效，其可靠性就难以达到总体要求的可靠性水平。所以在试验过程中，不允许出现1件失效，否则终止试验。试验无失效产品时且所有试验件的试验次数相同时，公式（1）可转化为下式评估产品的可靠性：

式中 γ——置信度，按某型号的可靠性大纲要求取0.7；n——投试样件数；m——形状参数，Weibull分布形状参数m取3；t0——规定任务时间（次数）；tR——试验截止时间（次数），即可靠寿命。

根据公式，可以推算出特定可靠性要求下的试验次数。为表达方便和统一化，这里的试验次数tR均相同，且取相对t0的相对次数，即在公式（2）中t0取为1，t为相对值。根据公式（2）可知，至少需要20倍的任务次数，才能评估出0.9995以上的可靠性，所以试验次数取20倍。

（6）可靠性试验方案及结果分析

按照地面试验模拟箭上工况的原则，设计了试验系统。试验系统如图3。

试验按照下列程序进行：

图3 试验系统示意图

①保持入口压力为22.6MPa，调整出口压力为1.5±0.3MPa。

②启动电磁阀，当减压阀入口压力从22.6MPa降至3.5MPa时，减压阀出口压力均应满足1.5±0.3MPa，不许有振动鸣叫现象。

③每完成10次试验后，从入口分别通入22.6MPa的气体，检查活门座和活门与其配合处的漏气量，其值不超过3L/min。

④每完成10次试验后，从入口分别通入1.28MPa气体，检查垫片和膜片密封处的漏气量，不许漏气。

（7）试验结果

2008年10月-12月，在北京宇航系统工程研究所增压输送系统试验室进行了减压器的可靠性试验。试验中，6件产品分别进行了80次试验，试验过程中和试验完成后的动作灵活性、密封性能均合格。因此可以认为所有试验件都没有损坏。试验结果见表1。

表1 试验数据表

根据公式（2），得到改进后减压器的可靠性评估结果为：

这一结果满足分系统分配的0.9995的可靠性指标要求。

6 结论

科学而先进的可靠性评估方法，为充分利用各种试验信息奠定了理论基础。这对减少试验经费，缩短研制周期，对合理安排试验项目，协调系统中各单元的试验量等有重要的作用。本文针对当前国内外阀门产品可靠性评估现状进行了调研分析，并根据载人航天运载火箭增压输送系统阀门产品的特点，制定了相应的可靠性评估方法，并以减压器为例，进行了可靠性评估方法的计算应用。

［1］吴辉.阀门的可靠性验证试验.阀门，1989

［2］乔刚.Reliability Analyse and Test Frequency Optimization of Motorized Isolation Valves of Emergency Core Cooling System.

［3］I.S.Grinberg and B.V.Karmugin.The reliability of safety valves［J］.chemical and petroleum engineering，1977.3.pp37-38

［4］Corwin L.Atwood.Parametric estimation of time-dependent failure rates for probabilistic risk assessment.Reliability Engineering&System Safety，Volume 37，Issue 3，1992，Pages 181-194

［5］Christian Kirchsteiger.Nonparametric estimation of time-dependent failure rates for probabilistic risk assessment.Reliability Engineering&System Safety，Volume 44，Issue 1，1994，Pages 1-9

［6］Knut Haugen，Per Hokstad and Heige Sandtorv.The analysis of failure data in the presence of critical and degraded failures.Reliability Engineering and System Safety，58（1997）97-107

［7］L.S.Kerimova.Improved Working Life in Plunger Oilfield Pump Valve Units［J］.Chemical and Petroleum Engineering，2006（42）：1-2.

［8］Marvin Rausand，Jorn Vatn.Reliability modeling ofsurface controlled subsurface safety valves［J］.Reliability Engineering and System Safety，1998（61）：159-166.

［9］中国电子技术标准化研究所.可靠性试验用表.北京：国防工业出版社，1987