关于算术编码教学的几点注记

王大星，朱鹤鸣

（滁州学院数学科学学院，安徽滁州 239000）

关于算术编码教学的几点注记

王大星，朱鹤鸣

（滁州学院数学科学学院，安徽滁州 239000）

随着科学技术的发展，信息、通信类本科生学习信息论是十分必要的。算术编码是基于统计的、无损数据压缩效率最高的编码方法。针对算术编码教学中存在的问题，本文进一步探讨了算术编码的编码、译码过程，提出了编码过程中需要注意的问题，并将算术编码与哈夫曼编码做了比较。最后，用Matlab实现了算术编码的具体实例。

算术编码；数据压缩；二叉树；哈夫曼编码

随着信息技术的发展，编码技术已经在媒体技术、网络技术、无线通信技术、数字电视技术等方面得到广泛应用。因此，信息与计算科学与电子信息类等专业的本科生应该具备一定的信息论基本理论以及信源、信道编码理论和技术等方面的基本知识。为了满足需要，许多高校在本科教学中开设了信息论与编码课程。信息论［1］［2］是一门应用概率论、随机过程和数理统计等方法来研究信息的存储、传输和处理中一般规律的学科。编码理论则与信息论一脉相承，它以信息论基本原理为理论依据，讲述编码的理论知识和实现方法。

算术编码在图像数据压缩标准（如JPEGJBIG）中扮演了重要的角色，是无失真变长编码的一种.算术编码中，消息用0和1之间的实数进行编码，该编码用到两个基本的参数：符号的概率和它的编码间隔.信源符号的概率决定了压缩编码的效率，也决定了编码过程中信源符号的间隔，而这些间隔包含在0到1之间.编码过程中的间隔决定了符号压缩后的输出。作者在教学过程中发现，教材中这部分内容介绍得相当粗略，定理的证明晦涩难懂，而且很少有例题分析。这些将导致学生在学习时显得很吃力。作者针对以上问题，结合多年来的教学经验探讨有关算术编码的教学问题，将教材中的理论细化，并作适当的延伸，以期给教师和学生带来些许帮助。

1 教学中采用二叉树解释算术编码的编译码过程

下面给出一个简化的计算程序来理解算术码编译码的基本要点。不是一般性，我们仅考虑二进信源，即信源字母集为χ＝｛0，1｝。对n长的信源字母列x n＝（x1，x2，…，x n）∈χn进行编码。

（1）先对所有x n∈χn，计算概率p（x n）＝p（x1，x2，…，x n）；

当信源是Markov信源时，p（x n）＝p（x1）p（x2｜x1）…p（x n｜x n－1）。

（2）在χn上建立一个字典序，对x n，yn∈χn，称x n＞y n，如果在第一个满足xi≠yi的第i个分量上x i＝1，yi＝0，这个条件等价于＞，也等价于它们对应的二进制小数0.

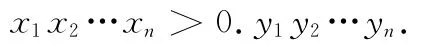
我们记x n（i）表示χn中在字典序下第i个n长的向量。

（3）用一个二叉树［4］来表示｛x n：xn∈χn｝，A为根节点，每个x n对应第n层上一个节点，那么从根节点到该节点的路上经过的边上的符号就是x1x2…x n。显然，按字典排序如果x n＞yn，其充分必要条件是x n对应之节点在y n对应的节点的右边。

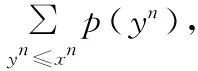
假设X1，X2…为无记忆信源，服从公共分布为伯努利分布，p（1）＝θ，p（0）＝1－θ.下面来计算F（1011010），如图1所示。

图1 计算F（1011010）二叉树图

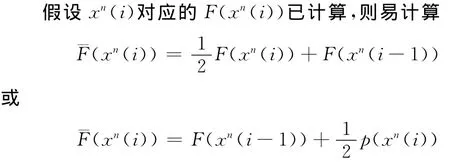
（5）译码时仍用树图逐层进行判决，假设从接收到的码字可计算出对应的F（x n），先从根节点开始比较F（x n）和p（0）。如果F（x n）＞p（0），则从0往下的子树在x n的左边，于是第一位译出x1＝1，反之若F（x n）＜p（0），则译出x1＝0。如果已经译出x1＝0，则继续比较F（x n）和p（00），如F（x n）＞p（00），则译出x2＝0。如此类推，直到译出最后一个x n为止。

2 算术编码教学中需要注意的问题

由于实际的计算机的精度不可能无限长，运算中出现溢出是一个明显的问题，但多数机器都有16位、32位或者64位的精度，因此这个问题可使用比例缩放方法解决。首先，算术编码器对整个消息只产生一个码字，这个码字是在间隔［0，1）中的一个实数，因此译码器在接受到表示这个实数的所有位之前不能进行译码。其次，算术编码也是一种对错误很敏感的编码方法，如果有一位发生错误就会导致整个消息译错。再次，算术编码可以是静态的或者自适应的。在静态算术编码中，信源符号的概率是固定的。在自适应算术编码中，信源符号的概率根据编码时符号出现的频繁程度动态地进行修改，在编码期间估算信源符号概率的过程叫做建模。需要开发静态算术编码的原因是因为事先知道精确的信源概率是很难的，而且是不切实际的。当压缩消息时，我们不能期待一个算术编码器获得最大的效率，所能做的最有效的方法是在编码过程中估算概率。算术编码的静态与自适应模型因此动态建模就成为确定编码器压缩效率的关键。最后，算术编码非常依赖计算机的计算能力和存储能力。过去，这种依赖极大地限制了它的发展，在提出的最初几年，算术编码压缩算法只在极小的范围内有原型实现。随着计算机科学技术的发展，许多算术编码的实现在执行速度上已经能够被人们接受［4］。如前面所说的那样，实现算术编码的核心问题在于如何获得正确的频率，以及如何高效地实现精确的乘法计算。

在算术编码高阶上下文模型的实现中，对内存的需求量是一个十分棘手的问题。因为我们必须保持对已出现的上下文的计数，而高阶上下文模型中可能出现的上下文种类太多了，数据结构的设计将直接影响到算法实现的成功与否。在1阶上下文模型中，使用数组来进行出现次数的统计是可行的，但对于2阶或3阶上下文模型，数组大小将依照指数规律增长，现有计算机的内存满足不了我们的要求。比较聪明的办法是采用树结构存储所有出现过的上下文。利用高阶上下文总是建立在低阶上下文的基础上这一规律，我们将0阶上下文表存储在数组中，每个数组元素包含了指向相应的1阶上下文表的指针，1阶上下文表中又包含了指向2阶上下文表的指针…由此构成整个上下文树。树中只有出现过的上下文才拥有已分配的节点，没有出现过的上下文不必占用内存空间。在每个上下文表中，也无需保存所有256个字符的计数，只有在该上下文后面出现过的字符才拥有计数值。由此，我们可以最大限度地减少空间消耗。

3 总结算术编码与哈夫曼编码的区别

哈夫曼编码属于码字长度可变的编码类，即从下到上的编码方法。同其他码字长度可变的编码一样，可区别的不同码字的生成是基于不同符号出现的不同概率。生成哈夫曼编码算法基于一种称为“编码树”的技术。算法步骤如下：① 初始化，根据符号概率的大小按由大到小顺序对符号进行排序。②把概率最小的两个符号组成一个新符号，即新符号的概率等于这两个符号概率之和。③ 重复第②步，直到形成一个符号为止，其概率最后等于1。④ 从编码树的根开始回溯到原始的符号，并将每一个下分枝赋值为1，上分枝赋值为0。

采用哈夫曼编码时有两个问题值得注意：① 哈夫曼编码没有错误保护功能，在译码时，如果码串中没有错误，那么就能一个接一个地正确译出代码。但如果码串中有错误，哪怕仅仅是1位出现错误，也会引起一连串的错误，这种现象称为错误传播。计算机对这种错误也无能为力，说不出错在哪里，更谈不上去纠正它。② 哈夫曼编码是可变长度码，因此很难随意查找或调用压缩文件中间的内容，然后再译码，这就需要在存储代码之前加以考虑。

而算术编码的基本原理是将编码的消息表示成实数0和1之间的一个间隔，消息越长，编码表示它的间隔就越小，表示这一间隔所需的二进制位就越多。算术编码用到两个基本的参数：符号的概率和它的编码间隔。信源符号的概率决定压缩编码的效率，也决定编码过程中信源符号的间隔，而这些间隔包含在0到1之间。编码过程中的间隔决定了符号压缩后的输出。给定事件序列的算术编码步骤如下：① 编码器在开始时将“当前间隔”［L，H］设置为［0，1］。②对每一事件，编码器按步骤A和B进行处理。A.编码器将“当前间隔”分为子间隔，每一个事件一个。B.一个子间隔的大小与下一个将出现的事件的概率成比例，编码器选择子间隔对应于下一个确切发生的事件，并使它成为新的“当前间隔”。③ 最后输出的“当前间隔”的下边界就是该给定事件序列的算术编码。

算术编码是一种到目前为止编码效率最高的统计熵编码方法，它比著名的哈夫曼编码效率提高10%左右，但由于其编码复杂性和实现技术的限制以及一些专利权的限制，所以并不像哈夫曼编码那样应用广泛。算术编码有两点优于哈夫曼码：① 它的符号表示更紧凑；② 它的编码和符号的统计模型是分离的，可以和任何一种概率模型协同工作。后者非常重要，因为只要提高模型的性能就可以提高编码效率。

哈夫曼码字必定是整数的比特长，这样就会产生问题：如一个符号的概率为0.3，则编码该符号的最优比特数大约是1.6，那么哈夫曼不得不将其码字设为1比特或2比特，并且每种选择都会得到比理论上可能的长度更长的压缩消息。而算术编码可以解决这个问题。算术编码是一种高效清除字串冗余的算法。它避开用一个特定码字代替一串输入符号的思想，而用一个单独的浮点数来代替一串输入符号，避开了哈夫曼编码中比特数必须取整的问题。但是算术编码的实现有两大缺陷：① 很难在具有固定精度的计算机完成无限精度的算术操作。② 高度复杂的计算量不利于实际应用。

算术编码是一种无失真的编码方法，能有效地压缩信源冗余度，属于熵编码的一种。算术编码的一个重要特点就是可以按分数比特逼近信源熵，突破了哈夫曼编码每个符号只不过能按整数个比特逼近信源熵的限制。对信源进行算术编码，往往需要两个过程，第一个过程是建立信源概率表，第二个过程是对信源发出的符号序列进行扫描编码。而自适应算术编码在对符号序列进行扫描的过程中，可一次完成上述两个过程，即根据恰当的概率估计模型和当前符号序列中各符号出现的频率，自适应地调整各符号的概率估计值，同时完成编码。尽管从编码效率上看不如已知概率表的情况，但正是由于自适应算术编码具有实时性好、灵活性高、适应性强等特点，在图像压缩、视频图像编码等领域都得到了广泛的应用。

4 算术编码的程序实现举例

Matlab语言是由美国MathWorks公司推出的计算机软件，经过多年的逐步发展与不断完善，现在已成为国际公认的最优秀的科学计算与数学应用软件之一，是近几年来在国内外广泛流行的一种可视化科学计算软件。它集数值分析、矩阵运算、信号处理和图形显示于一体，构成了一个方便的、界面友好的用户环境，而且还具有可扩展性特征。在本文中，所用到的算术编码就可以用Matlab进行实现。Matlab的语法规则比C语言等高级语言更简单，更重要的是贴近人的思维方式的编程特点。所以，在我们进行图像压缩时，这是一种很好的方法。

软件运行步骤：单击“MATLAB”图标－“file”－“New－M－file”，编写好源程序之后，运行程序仿真即可。

下面我们用Matlab工具举例实现算术码的一个例子。其程序如下：

5 结束语

随着信息技术的发展，各种媒体信息（特别是图像和动态视频）数据量非常之大。从家庭娱乐到专业的通信设备、从廉价的消费电子产品到昂贵的专业设备，应用的例子举不胜举。算术编码作为一种高效的数据编码方法在文本，图像，音频等压缩中有广泛的应用，甚至还可以将它应用于文件的加解密［5］。算术编码从性能上看具有许多优点，特别是由于所需的参数很少，不像哈夫曼那样需要一个很大的码表，常设计成自适应算术编码来针对一些信源概率未知或非平稳情况。但是在实际实现时还有一些问题，如计算复杂性，计算的精度以及存储量等，随着这些问题的解决，算术编码正在进入实用阶段，但要扩大应用范围或进一步提高性能，降低造价，还需进一步改进。所以，研究算术编码有非常好的前景与实用价值。

［1］朱雪龙.应用信息论基础［M］.北京：清华大学出版社，2001.

［2］沈世镒，吴忠华.信息论基础与应用［M］.北京：高等教育出版社，2005.

［3］严蔚敏.数据结构（C语言版）［M］.北京：清华大学出版社，2007.

［4］仇佩亮.数字通信基础［M］.北京：电子工业出版社，2007.

［5］赵风光，倪兴芳.算术编码与数据加密［J］.通信学报，1999，20（4）：92－96.

Remarks on Arithmetic coding Teaching

Wang Daxing，Zhu Heming
（Department of Mathematics of Chuzhou university chuzhou 239012，China）

With the development of science and technology，it is necessary for the students of specialty on information science and communication technique to learn the course of Information Theory and Coding Theory.Arithmetic coding is the most powerful technique for lossless data compression.For problems in arithmetic teaching，the paper shows the process of arithmetic coding and decoding，illustrating with specific examples.The problems which needs attention in coding are proposed，and compared with the Huffman coding.Finally，we achieved specific examples of arithmetic coding with Matlab.

Arithmetic coding；Data compression；Binary tree；Huffman coding

TP301

A

1673－1794（2011）05－0097－04

王大星（1980－），男，硕士，讲师，研究方向：密码学。

滁州学院应用数学省级教学团队项目；安徽省高校省级自然科学研究项目（KJ2011Z277）；滁州学院科研基金资助项目（2010kj009B）

2011－04－19