融入多元因素促进高等数学教学改革
2011-11-13方芳
方 芳
(滁州学院 数学科学学院,安徽 滁州 239000)
融入多元因素促进高等数学教学改革
方 芳
(滁州学院 数学科学学院,安徽 滁州 239000)
将多元因素融入高等数学的教学中,可以提高教学效果满足社会要求。这里的多元因素包括数学史、计算机媒体、数学建模思想。将数学史融入高等数学的教学中的策略有:故事策略、方法比较策略、追踪历史起源策略、揭示思维过程策略;将计算机媒体技术融入高等数学教学中的方法有:制作教学课件代替传统板书、制作三维图形、利用MatLab符号工具箱直接求解、利用MatLab动画演示、进行适当的数学实验、播放专家讲座视频、建立习题库;将数学建模思想融入高等数学教学中的方式有:在绪论课中、在概念讲授中、在定理和公式讲授中、在课堂例题中和在课外习题中渗透数学建模思想。
高等数学教学;数学史;计算机媒体技术;数学建模思想
1 高等数学教学改革的必然性
数学越来越成为一种普遍的科学语言与工具,在推动其他科学和整个文化的进步方面起着不可替代的巨大作用。高等数学作为高等院校的一门重要的基础学科,它不仅为学生学习后继课程和从事所学专业工作提供必备的数学基础知识和方法,而且在培养学生逻辑思维、分析问题与解决问题的能力方面具有重要的不可替代的作用。[1]但目前高等数学教学中存在着内容多、难度大、课时少,与学生所学的专业联系不够紧,教学以考试为目的,教学手段单一、与实际联系脱节,学生没有学习兴趣等问题。为了解决这一矛盾,一场高等数学教学改革势在必行。
2 将多元因素融入高等数学教学中
2.1 将数学史融入高等数学教学中
[2]数学史是高校数学专业高年级的一门选修课,同其他学科历史一样,其研究内容可以让我们了解和熟悉该门学科发展的历史事实,把握在其历史发展过程中的特点和规律。学习数学史,可以使我们追根溯源,培养史学观念,可以使我们全面深刻地理解数学知识,领略重要的数学概念、命题、思想、方法形成的历史进程,从而极大地提高数学素养,正如文中所说,“数学史对于揭示数学知识的现实来源和应用,对于引导学生体会真正的数学思维过程,创造一种探索与研究的数学学习气氛,对于激发学生学习数学的兴趣,培养探索精神,对于揭示数学在文化史和科学进步史上的地位与影响进而揭示其人文价值,都有重要意义。”以下列出数学史融入高等数学教学中的几种策略。
2.1.1 故事策略
虽说数学史不等于数学故事。但是,数学家或数学界的遗闻佚事,不仅能大大激发学生的学习兴趣,而且对学生的人格成长还富有启发作用。说故事的目的就是要设计一个教学情景,这个教学情景主要是能引起学生的学习动机与兴趣。同时,也可利用故事情景引出学生已有的数学概念,或是借故事情节引入要教的数学概念,也可以利用故事情节的铺设,呈现给学生想要解决的问题等。
2.1.2 方法比较策略
事实上,高等数学教学中涉及的许多问题,从它的历史到现在,经过数代数学家们的不懈努力,大都产生过不少令人拍案叫绝的各种解法。如割圆法、现代的微积分方法,还有定理的不同种证明方法,通过搜集比较历史上的各种不同方法之后,不仅能使学生更好地领会每种方法的内在本质,而且能启发学生,这对培养知识面宽、有能力、有信心、灵活多变的人大有帮助。
2.1.3 追踪历史起源策略
数学固然起源于人类对日常生活现象的观察,但它决不简单,有一定的难度,需要时间去体验、把玩并体会它的意蕴。譬如函数概念的发展,从笛卡尔给出最简单的函数概念出发,经莱布尼兹、贝努利、欧拉、柯西、黎曼、狄利克雷、维布伦等人之手,一步一步的发展,其间经历了大约六七次扩充,才形成了我们今天看到的函数概念。追踪历史起源,就是要引导学生去揭示或感受知识发生的前提或原因、知识概括或扩充的经过以及向前发展的方向,引导学生在重演、再现知识发生过程的活动中,内化前人发现知识的方法和能力。使学生在掌握知识的同时,还能占有镌刻于知识产生中的认识能力,这种认识能力正是构成创新思维能力的核心。
2.1.4 揭示思维过程策略
将数学研究中的思想和方法的要点原原本本地告诉学生,引导青年学生沿着科学的艰险道路作一次富有探索精神的、充满为真理而斗争的崇高动机的旅行,使学生充分领略以前数学大师们的灵感,承受他们的启迪,可以从中学到他们的策略和经验等。譬如,结合几何知识的学习,可以向学生揭示历史上有关几何第五公设的、令一代又一代数学家忙碌了二千多年的、各种各样的思考过程及最终的解决办法。让数学史曾闪烁过光芒的火花,重新在学生的心中点燃。
2.2 将计算机媒体技术融入高等数学教学中
随着计算机的日益发展和普及,计算机越来越多地被应用到大学教学中,成为教师们得力的教学辅助工具。多媒体教学突破传统教学方式的局限,从根本上改变了大学教学的面貌,它通过声音、图像、文字、动画的立体式教学给学生营造一个良好的示范环境,使得教与学变得形象和生动,让学生获得最直观的文化信息,激发学习兴趣,大大提高了大学教学质量。下面列出如何将计算机媒体技术引入高等数学教学中。
2.2.1 制作教学课件代替传统板书,使教学更高效
譬如课堂一开始,教师就可以通过PPT的形式将该节课所要讲述的内容先进行一个列举,使学生们可以清楚的知道自己这节课要掌握什么内容。而且对于一些概念,公式都会有一个比较直观的理解。
2.2.2 制作三维图形,使空间图形更加立体、直观
空间解析几何是高等数学中的重要组成部分,对空间解析几何中一些典型曲面与曲线的图形准确绘制对多元微积分的学习非常重要,现有的教科书中虽有不少曲面和曲线的插图,但数学教师大多都没有受过斜投影作图法的训练,要他们在黑白的一维平面上徒手绘出三维空间的曲面和曲线既费力又费时,实在勉为其难,且往往不能准确地表达立体图的效果,因而在一定程度上会影响教学效果。但如果利用计算机就可以制作视觉立体的三维图形,而且还可以执行动态的转动、变化等操作,使学生对图形的结构关系形成变化趋势有更自观的认识。
2.2.3 利用MatLab符号工具箱直接求解可省去大量计算步骤
函数的极限、单变量与多变量函数在函数微积分、常微分方程的问题的直接求解是高等数学的重要内容。利用MatLab软件的符号运算工具箱可以直接求解这些问题的解析解,这样就省去了大量繁琐的计算步骤,从而节约了很多时间可以进行其他问题的研究。
2.2.4 利用MatLab动画演示使讲解更形象生动
在空间解析几何和多元函数微分学的教学过程中经常需要借助多元函数图形来理解,而教材所给的往往是静态的平面图形,学生无法建立起空间图形的概念,因此在该部分内容教学过程中可以适当使用MATLAB动画来建立三维空间的函数图形,演示一些抽象结论的形成过程,让学生更容易理解和掌握。
2.2.5 利用计算机进行适当的数学实验,培养学生对数学的兴趣
数学实验是计算机技术和数学软件引入教学后出现的新事物。数学实验的开展可以在数学教育中体现学生的主体意识,让学生做到会学、会用、会做数学,提高学生学习数学的积极性,提高学生对数学的应用意识,并培养学生用所学的数学知识和计算机技术去认识问题和解决实际问题的能力。
2.2.6 播放专家讲座视频,使学生对某个知识点有更深刻的认识
如果就某个知识点让学生自己去看相关书籍,学生很有可能会感觉乏味。因为书籍是静态的,没有互动的,况且专业性太强,不易于理解,学生往往不能坚持看完。但是引入视频讲座之后,就会起到不一样的效果。视频的动态画面,声音效果都能引起学生的注意并加深对知识点的印象。
2.2.7 借助计算机建立习题库
为减轻教师重复劳动,解除教师因每年设计学生练习、考试题而疲于奔波“题海”之苦,教师间或教研组可齐心协力设计、筛选题目,再将精心设计的题目按课时、章节、单元、专题知识在计算机上分类建立习题库,按教学层次及学生知识层次建立难易有别的试题库,并附有合理的评分标准及学生掌握情况统计等,使教师有“用则取,用后比”之便。当然,习题库与试卷库还存在不断取舍与补充的必要,目的使题库更精要,更实用,更新颖,更具有对应性与针对性。
2.3 将数学建模思想融入高等数学教学中
凡是将具体现象、事物的特征和性质给以数学表达的数学结构,叫数学模型。即以解决某个现实问题为目的,从该问题中抽象、归纳出来的数学问题就称为数学模型。数学建模就是数学模型建立的过程。建立数学模型的步骤可以用下面的框图1表示。
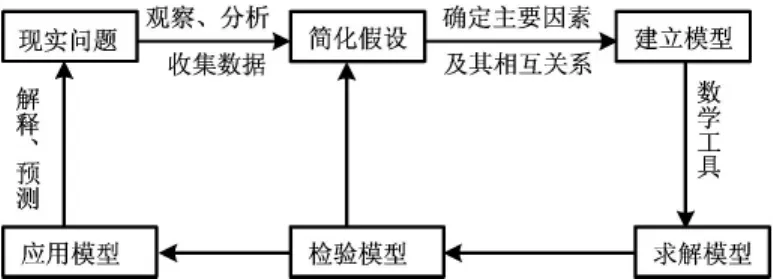
图1 框图
通过把数学建模的思想方法融入到高等数学的教学环节中,其目的是要促进学生更好地学习和掌握高等数学的基本知识,提高学生的数学应用意识和创新能力,在实施教育过程中应当正确处理好教学的“严谨性”和“实用性”之间的关系,促进教学改革的良性发展。那么怎样在高等数学教学中渗透数学建模思想呢?
2.3.1 在绪论课中渗透数学建模思想
爱因斯坦曾说过:“兴趣是最好的老师”,通过一次好的绪论课教学,可以使学生认识到高等数学的重要性和必要性,让学生了解所学知识的来龙去脉和历史渊源,有助于激发学生的求知欲望,顺利步入高等数学学习的殿堂。在讲高等数学的绪论课时,可向学生简介微积分的前期史,使学生知道,微积分产生于17世纪,微积分的诞生并非一两个人的功劳,它是17世纪许多伟大的数学家经过漫长而曲折的奋斗过程而取得的成果。了解这一历史,学生将不仅获得真知灼见,还将获得探寻科学真理的勇气,这对于克服学习数学和数学建模中可能遇到的困难是十分有益的。
2.3.2 在概念讲授中渗透数学建模思想
数学概念是因为实际需要而产生的,是从客观事物的数量关系中抽象出来的数学模型。在数学教学中应重视从实际问题中抽象出数学概念的过程,培养学生应用数学的兴趣。具体来讲,高等数学教材中的概念都是从客观事物的某种数量关系或空间形式中抽象出来的数学模型,概念是其他相关定理和应用的前提。因此,在教学中应让学生知道所学概念是从怎样的实际“原型”中抽象出来的,要让学生感觉到教材里的概念是自然而然的流淌出来的,而不是生硬规定的。教师在讲授象极限、导数、连续、定积分等概念时,应设置适宜的生活问题情境,结合数学建模的思想和方法来引导学生参与教学活动。
2.3.3 在定理和公式讲授中渗透数学建模思想
高等数学中定理的证明是教学过程的一大难点。事实上教材中的很多定理,在开始的时有其直接或间接的背景,经过抽象之后成为了定理。因此,在教学中让学生能在一定程度上了解所学知识的来龙去脉及历史渊源,把定理的结论看作是一个特定的更加抽象的模型,这是非常重要的。要达到此目的,结合数学建模的思路和方法,把定理的条件看作是模型的假设,根据预先设置的问题情景引导学生一步一步地发现定理的结论。这种教学方法,不但使学生学到知识,而且让他们体验到探索、发现和创造的过程,是培养学生创新意识和能力的一个好途径。
2.3.4 在课堂例题中渗透数学建模思想
在课堂教学中,以具体案例作为教学内容,通过具体问题的建模范例,介绍数学建模的思想方法。既巩固了所学知识,又提高了教学的趣味性,也极大地调动了学生学习的积极性,使学生觉得数学既有趣又有用。这样既使学生掌握数学建模的方法,又使他们深刻体会到数学是解决实际问题的锐利武器,有利于教学中贯彻理论和实际相结合的原则,培养增强学生的想象力,洞察力和创造力。
2.3.5 在课外习题中渗透数学建模思想
在作业中布置一些结合学生专业特点,有生产、生活实际背景和较好的应用价值,使学生真正体会到数学的科学性和实用性,达到既有助于理解教学内容,又可以通过对实际问题的抽象、归纳、思考,用所学的数学知识给予解决的目的开放型的应用题,给学生以更大的思维空间,促进数学思想的进一步完善。通过完成这种作业,使学生感受到数学应用之所在,这样,学生完成作业就不再是以“练”为主,而是以“做”为主,通过“做”来体验数学,认识数学,掌握数学建模的思想方法。例如,在学习“常微分方程”一章时,介绍“马尔萨斯”人口模型,课后可以让学生根据现代人口发展的状况,分析、研究其他人口学家提出的改进以后的人口模型,并进行检验。
为了适应社会发展的需要,高等数学教学改革势在必行,而教学改革的先行者和执行者是教师。教师必须不断汲取新鲜的知识,及时更新教学方法和手段,提高教学效果。通过高等数学的教学,应使学生在掌握了足够的知识同时,培养他们的创新意识和求真务实的品质。当然在高等数学教学改革中仍然会出现很多的问题,高等数学教学改革任重而道远,积极推进数学教学改革,努力提高数学课程的教学质量,是我们每一位数学教育工作者的职责和追求。我们将不断探索和实践,为培养高素质的科技人才贡献自己的力量。
[1]梁伟,李朝晖,余维虹.高等数学教学改革探讨[J].河海大学常州分校学报,1998,(3):12.[2]王永亮 .在高数教学中融入数学史教育的探究[J].信息系统工程2010,(7):85.
[3]方坤夫.计算机辅助大学数学教学[J].湖州师范学院学报,1998,(6):13.
[4]程庆霞.对高等数学教学中渗透数学建模思想的探讨[J].职业时空,2007,(19):13.
[5]李排昌.对《高等数学》教学改革的几点建议[J].公安大学学报(自然科学版),2000,(3):13.
[6]康永强 .《高等数学》课程改革探索与研究[J].长江大学学报(社会科学版),2010(4):179.
[7]马离军.对高等数学一些教学方法的探讨[J].内蒙古科技与经济,1999,(6):12.
[8]刘小琼,刘新乐.高职数学教学改革的几点思考[J].科技信息,2008,(27):211.
[9]张小美,施声久.关于高等数学教学改革的探讨[J].南通工学院学报(社会科学版),2002,(2):19.
[10]郝彩丽.对我区高等数学教学改革的探讨[J].西藏科技,2004,(11):25.
G642
A
1673-1794(2011)05-0094-03
方 芳,女,讲师,理学硕士,研究方向:动力系统。
滁州学院教研课题大学数学教学团队资助项目(2010jyy003)
2011-03-12
