基于Contourlet变换的MRI医学图像增强

石永华

（滁州学院 机械与电子工程学院，安徽 滁州 239000）

基于Contourlet变换的MRI医学图像增强

石永华

（滁州学院 机械与电子工程学院，安徽 滁州 239000）

利用Contourlet变换的多尺度、局部化、方向性等优点，提出一种基于Contourlet的MRI图像增强方法。实验结果表明，与传统的方法相比，该方法能够更有效地增强MRI图像的边缘细节特征，获得良好的效果。

MRI；图像增强；Contourlet；循环平移

磁共振成像（Magnetic Resonance Imageing，MRI）可以很好地识别大脑的灰质和白质密度接近的软组织，从而深受医生的青睐，其临床应用越来越广。然而受其他因素影响，原始的MRI图像可能出现值脉冲噪声、伪影、图像模糊等，因此需要对MRI图像进行增强处理，凸显重要的医学特征，改善图像的质量，以方便医生对病情做出准确的判断。

目前，国内外文献中关于MRI图像增强方法的研究，大部分集中于小波变换。在对图像增强的同时，也增强了噪声信号［1］，使得图像的弱边缘与噪声难以区分，从而引起细节模糊、对比度差等问题。本文提出一种基于Contourlet的MRI医学图像增强方法。该方法采用Contourlet变换来分解和重构MRI图像，用非线性增强函数对图像高频部分做增强处理，获取高质量图像，以便提高医生诊断的正确率。

1 Contourlet变换

为了有效地表示图像，Olshausen＆Field提出了稀疏表示的方法［2］。稀疏表示要求图像线性展开中大部分基函数的系数为零，只有少数基函数具有较大的非零系数。也就是说，某种表示方法是“稀疏的”表明：一数值较大的系数集中 （浓缩）了图像的大部分能量和信息，意味着使用少量的比特数就能达到表示图像的目的。小波变换能够高效地对一维分段连续信号进行分析。由一维小波张成的二维可分小波基具有正方形的支撑区间，只具有有限的方向，即水平，垂直，对角三个方向［3］，因而不能“最优”表示图像。小波在表示具有点奇异性的函数时是最优基，但是对于MRI图像而言，小波基并不是最优基，不能有效地挖掘图像中的边缘方向信息，非线性逼近性能弱，最终表现为不能“稀疏”表示MRI图像。

2002年M.N.Do提出了一种“真正”的图像二维表示方法：Contourlet变换［4］，也称为塔形方向滤波器组（Pyramidal Directional Filter Banks，PDFB）。Contourlet变换是一种多尺度、局部化、方向性的图像表示方法。它的基的支撑区间是随尺度而长宽比变化的长方形结构，类似于轮廓段，具有小波变换不具备的方向性和各向异性，对于图像中细小的有方向的轮廓和线段的表达具有很大的优势。相比较小波变换而言，Contourlet变换表示图像边缘的系数能量更加集中，获得非常好的非线性逼近性能，因此对MRI图像能够进行更好的稀疏表示。如下图1所示。

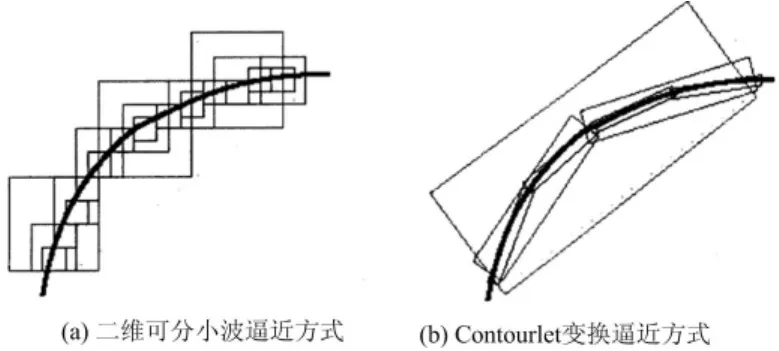
图1 稀疏表示方法

Contourlet变换的实现由两个步骤进行，子带分解和方向变换［5］。第一步是由 LP变换（Laplacian Pyramid，LP）对图像进行多尺度分解以“捕获”点奇异，产生原始信号的低通采样逼近和原始信号与预测信号的差值，对得到的低通图像继续分解得到下一层的低通逼近和差值图像，如此逐步滤波得到图像的多分辨率分解。第二步由方向滤波器组（Directional Filter Banks，DFB）将分布在同一方向上的奇异点合成为一个系。Minh N.Do提出了一种新的分解实现方法［6］，包括两个模块：第一层是两通道的梅花滤波器组，第二层是一个象限滤波器。该方法使用扇形结构的双通道共轭镜像滤波器组并在滤波前后结合错切操作得到不同方向的频带剖分，如图2所示。

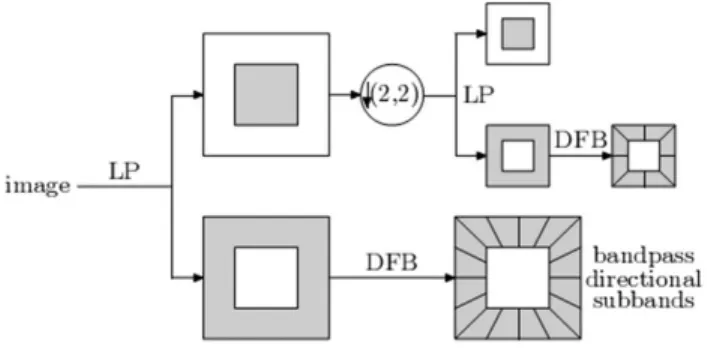
图2 Contourlet变换滤波器组结构图

2 MRI图像的增强算法

2.1 循环平移Cycle Spinning

在对MRI图像进行处理时，Contourlet的滤波器结构

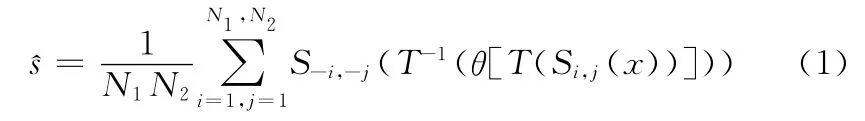
式中：N1，N2是最大平移量，S是循环平移算子，下标i，j，－i，－j分别为行和列方向上的平移量，T为变换算子，T－1为逆变换算子，θ为增强算子。MRI图像通常有较多的奇异点，对于a奇异点平移是最佳的，而对于b奇异点这个平移是最差的，这样就引起矛盾。CS方法采用对多次循环平移处理的结果取平均来解决此类问题，减小或消除奇异点附近产生的伪Gibbs失真，减弱了MRI图像中的伪影现象，达到改善重构图像质量的效果。

2.2 评价方法

图像质量的含义［9］包括两个方面：一个是图像的逼真度，描述被评价图像与标准图像的偏离程度；另一个是图像的可懂度，是指图像能向人或机器提供信息的能力。目前为止，并没有统一的评价标准来评价图像。本文基于MRI图像进行增强处理，根据其特征需要，采用了熵（Entropy）、均方根误差（RMSE，root mean square error）、清晰度（Definition）等来进行评价［10］。

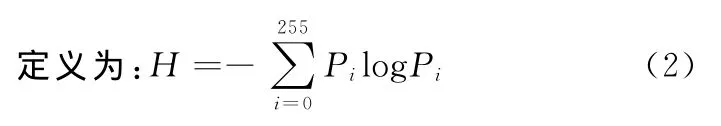
（1）熵缺乏平移不变性，在边缘处和重要细节部分会出现伪Gibbs失真。为了解决这一问题，可以对图像进行“循环平移——阈值去噪——逆方向循环平移”在一定范围内对信号进行循环平移，对每个平移量的结果进行阈值去噪，然后分别对平移后的数据做增强，再将处理后的数据反平移，对多次处理的结果取平均。这就是Coifman和Donoho提出 Cycle Spinning方法（CS方法）［7］［8］，表示为

Pi为像素灰度为i的概率。熵越大，反映了图像携带的信息量越大，图像的细节表现力越强。

（2）均方根误差

设xR为原始图像，xE为增强后的图像，（M，N）表示为图像大小，则：

均方根误差：

RMSE值越大，增强前的图像与增强后的图像之间的差异越大，在一定程度上可以表示原始图像被增强的程度越大。

（3）清晰度（Definition）：

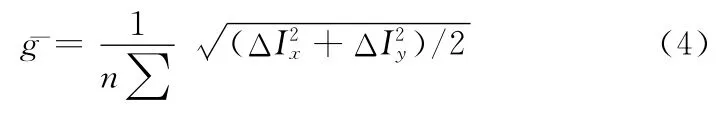
其中，ΔIx和ΔIy分别表示x和y方向上的差分，n表示图像的大小。清晰度反映了图像中的微小细节反差和纹理变换特征。¯g越大，说明最后获得的图像越清晰。

2.3 增强算法描述

小波变换应用于MRI图像处理的研究很多，Contourlet在此方面的应用尚在探索之中。文中将Contourlet变换引入到 MRI图像增强领域，将CS方法引入到Contourelt中，以抑制由于Contourlet变换缺乏平移不变性产生的伪Gibbs失真现象。对于进行Contourlet变换分解后的各种系数，算法中采用A.F.Laine提出的增强函数来处理，计算所需的非线性方程是f（x）＝axmax［sigm（c（x／xmax－b））－sigm（－c（x／xmax＋b））］［11］。其中，参数b是增强范围，一般取0～1之间；参数c是控制增强强度，一般取20～50之间。

根据上述分析，本文提出了一种基于Contourlet变换的MRI图像增强算法，具体算法步骤为：

（1）对 MRI图像用Cycle Spinning作n次循环平移，n根据需要而定，本文定为8次。

（2）对循环平移后的图像进行Contourlet变换，得到不同尺度不同方向上的变换系数。算法中选用不同的波基和滤波器进行多次试验，根据运用评价指标获得的数据对比，得出结果：使用sym8小波和9－7滤波器获得的各项数据值最大。

（3）对于不同的变换系数，根据阈值公式计算阈值，再根据非线性方程确立增强范围b和增强的强度c的值。本文通过反复试验选取b＝0.15，c＝20，此时效果最好。

（4）对增强后的变换系数进行Contourlet反变换，重构图像，得到增强的图像。

（5）最后评价图像。利用清晰度、均方根误差、熵等指标对获得的图像进行质量评价。

2.4 实验结果及对比分析

实验中选用基于小波变换的增强算法（A方法）、本文算法（B方法）对多幅MRI图像进行增强处理，并使用3.2的图像质量评价指标来分析。（限于篇幅，本文仅列出两副图像及两种算法的增强图像。）本文算法利用 Matlab6.5编程实现，运行环境CPU P4 2.4G，内存512MB，操作系统Windows XP（SP3版）。

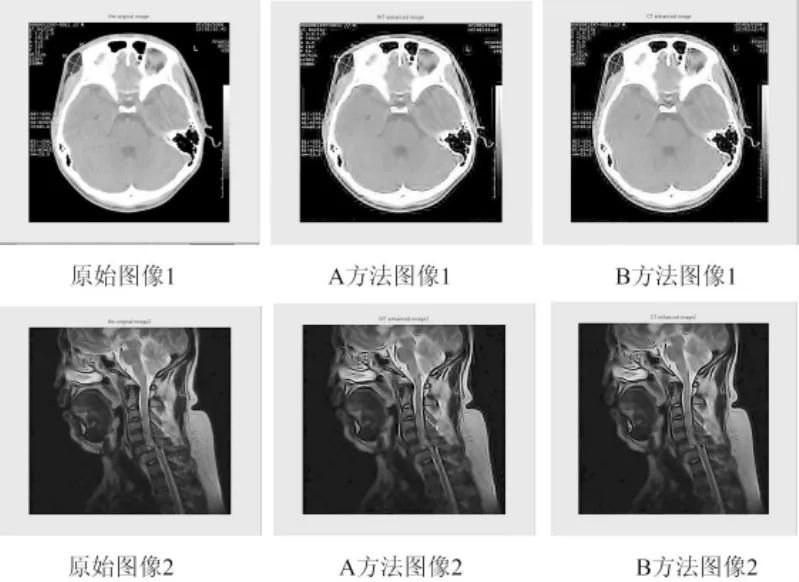
图3 A、B不同算法的结果对比

对上述图像运用3.2的评价指标进行分析，获得的数据如下表1所示：

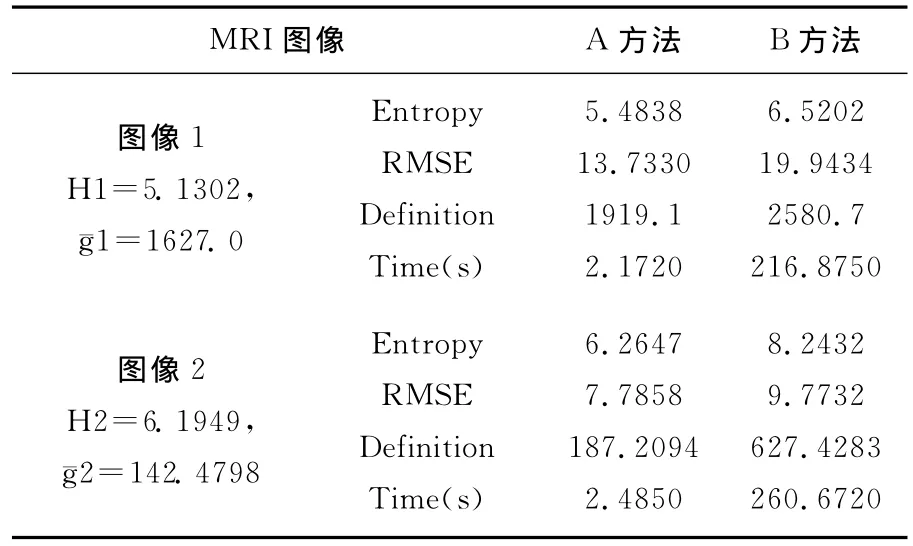
表1 实验获得的数据

图4 实验数据的图表表示

通过比较两种方法的均方根误差、熵和清晰度可以得出结论：本文方法的三项指标都比已有方法的要大。B方法的均方根误差大，说明图像被增强的程度较大；熵大，说明图像携带的信息较多，图像细节表现力较强；清晰度大，说明处理后图像的重要特征更加清晰。为得到高质量的图像，本文提出的算法比小波变换（WT）稍显复杂，运行时间比WT方法要长，然而其增强效果却是明显的。以样本图像2颈椎图像为例，原始图像比较模糊难以辨认。经过本文算法处理后，图像清晰度增大、各项特征明显，医生很容易识别并得出患者颈椎骨折脱位伴有脊髓损伤的医学结论。

3 结束语

本文算法可以很好地增强MRI图像的重要特征和细节分量，方便了医生作出准确的诊断，是一种有效的图像增强方法。但是如何提高算法的实时性，仍然是今后需要进一步研究的问题。

［1］闫敬文，屈小波.超小波分析及应用［M］.北京：国防工业出版社，2007.

［2］焦李成，谭 山.图像的多尺度几何分析：回顾和展望［J］.电子学报，2003，31（12A）：1975－1981.

［3］成礼智，王红霞，罗 永.小波的理论与应用［M］.北京：科学出版社，2004.

［4］Do MN，Vetterli M.The contourlet transform：an efficient directional multiresolution image representation ［J］.IEEE Transactions Image on Processing，2005，14（12）：2091－2106.

［5］Do MN，Vetterli M.Contourlet：A directional multiresolution image representation［A］.Proc of IEEE International Conference on Image Processing［C］.Rochester，NY：2002，357－360.

［6］刘 海，杜锡钰，裘正定.四方向上的任意角度扇形数字滤波器的设计.通信学报，1994，15（4）：11－20.

［7］Ramin Eslami and Hayder Radha.The Contourlet transform for image denoising using Cycle Spinning［C］.Signals，Systems and Computers，the Thirty－Seventh Asilomar Conference，2003，1982－1986.

［8］梁 栋，沈 敏.一种基于Contourlet递归Cycle Spinning的图像去噪方法［J］.电子学报，33（11），2005：2044－2046.

［9］袁杰灰.图像质量评价方法综述［J］.计算机工程与应用，1998，93－105.

［10］冼广铭，王知衍，黄 鲲.紧支撑二维小波多尺度融合图像效果评价［J］.计算机工程与设计.2006，27（15）：2740－2743.

［11］Andrew F.Laine，Sergio Schuler，Jian Fan，Walter Huda.Mammographic feature enhancement by multiscale analysis［J］.IEEE Transactions on medical imaging，1994，13（4）：725－752.

On MRI Medical Image Enhancement Based on Contourlet Transform

Shi Yonghua

（School of Mechanical and Electronic Engineering，Chuzhou University，Chuzhou 239000，China）

Contourlet transform is a new kind of image representations which is of multi－resolution，local supporting and multi－direction.A new algorithm of the MRI image enhancement using Contourlet transform is proposed.Simulation experiments were carried out.The experiments show that the algorithm proposed gets good results and enhances the images details and texture compared to the traditional algorithm.

Magnetic Resonance Imaging；image enhancement；Contourlet；Cycle Spinning

R445

A

1673-1794（2011）05-0047-03

石永华（1975－），男，硕士，讲师，研究方向：数学图像处理。

滁州学院自然科学研究项目（2008kg021B）

2011-08-10