二阶延迟微分方程单支θ－方法的渐近稳定性

陈志兴，殷雪剑

（安徽大学 数学科学学院，安徽 合肥 230039）

二阶延迟微分方程单支θ－方法的渐近稳定性

陈志兴，殷雪剑

（安徽大学 数学科学学院，安徽 合肥 230039）

考虑二阶微分方程单支θ－方法的稳定性质，证明当θ＝1时数值方法将保持此时滞系统解析解 的稳定性。

二阶延迟微分方程；稳定性；单支θ－方法

1 二阶延迟微分方程的稳定性

近几年，二阶延迟微分方程的解析解和各种数值方法的渐近稳定性一直引人关注，如文献［1－4］，但对于微分方程

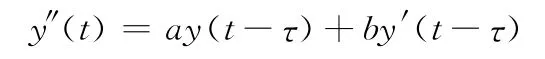
的研究却未涉及，所以本文主要对上述方程的解析解及单支θ－方法的稳定性进行研究，得到保持其渐近稳定的充要条件。

考虑如下方程

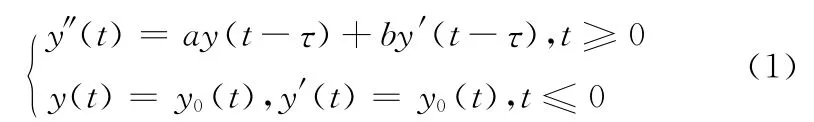
其中a，b是非零实数，τ＞0是常延迟量。（1）的特征方程为

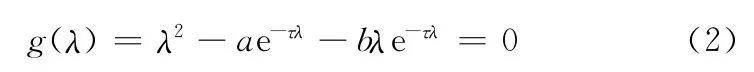
定义1 方程（1）被称为渐近稳定的，当且仅当其任意解满足lim

t→∞y（t）＝0.

引理1［5］特征方程（1）具有负实部的充要条件为

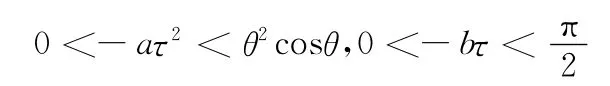
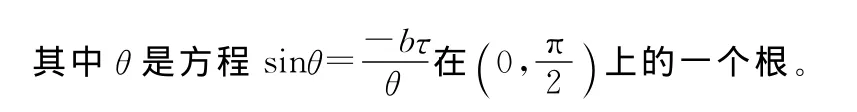
由于中立型方程的特征根可能以±i∞为聚点，尽管（1）的特征根λ满足Re（λ）＜0，但仍然会产生（1）的解y（t）无界（t→∞）。因此，按照 Miranker［6］的结论，有下面结论：

定理1 方程（1）被称为渐近稳定的，当且仅当方程（2）的所有零点λ满足

Re（λ）≤－r＜0

定理2 方程（2）的所有零点λ满足Re（λ）≤－r＜0的充要条件为

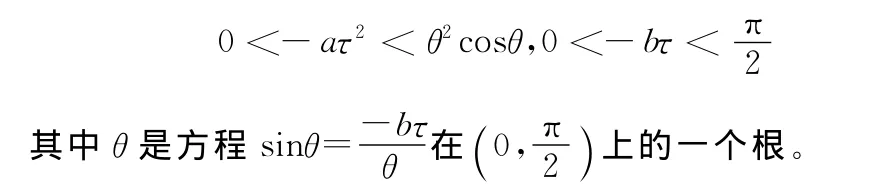
证明 根据引理1，下面仅需证明方程（2）的零点是一致地离开虚轴的。

考虑函数

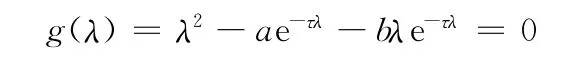
由于g（λ）是非多项式的整函数，根据Picard的整函数零点分布定理，所以有可数无限个零点λ1，λ2，λ3，…且λn→∞，n→∞.假设存在数列｛λn｝是方程（2）的零点，但不是一致地离开虚轴，那么

两边取极限，有

从而产生矛盾。

所以，方程（2）的零点一致地离开虚轴的。

2 单支θ－方法的稳定性

考虑y′（t）＝f（t，y（t），y（φ（t））），应用单支θ－方法（参见文献［7］）求解，得到迭代式

其中θ∈［0，1］，yn表示对精确解y（tn）的数值近似且当t＞0时，通过分段线性插值

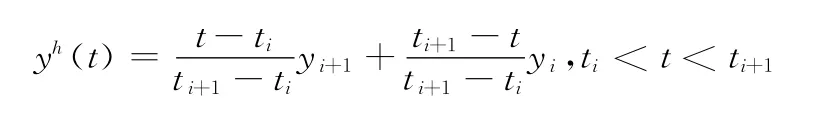
为了研究二阶延迟微分方程（1）的数值稳定性，考虑等价系统

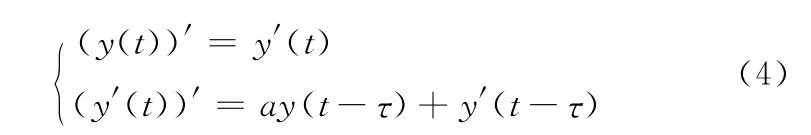
应用单支θ－方法（3）求解上述方程，有

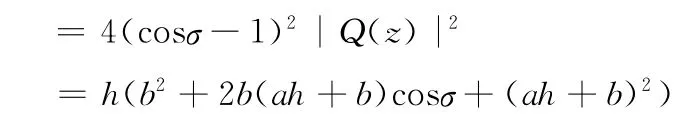
由定理1，有a，b＜0，显然有Q（z）＝0根的模小于1（h＞0）。由条件（5），则对｜z｜＝1，有｜Q（z）｜＞｜Pm（z）｜，根据Rouche定理，特征多项式p（z）是schur多项式，从而有θ＝1时，单支θ－方法是渐近稳定的。

［1］葛淑君.二阶延迟微分方程θ－方法数值解稳定性［J］.哈尔滨师范大学自然科学学报，2006，22（3）：29－30.

［2］徐 阳，赵景军.Volterra型时滞积分方程单支θ－方法的稳定性［J］.数学物理学报，2008，28A（5）：942－944.

［3］郭长勇，赵景军，刘明珠.二阶延迟微分方程解析解的渐近稳定性［J］.黑龙江大学自然科学学报，2002，19（3）：5－7.

［4］范振成.二阶延迟微分方程数值稳定性研究［J］.哈尔滨工业大学硕士学位论文，2000，7.

［5］Bellman R，Cooke K.L.Differential－difference Equations.New York：Academic Press，1963.

［6］W.L.Miranker.Existence，uniqueness and stability of solutions of systems of nonlinear differential equations.J.Math.Mech.，1962，11：101－108.

［7］Liu Y.K.Stability analysis ofθ－methods for neutral functional－differential equtions.Numer Math，1995，70：473－485.

Stability of One-legθ-methods for Second-order Delay Difference Equations

Chen Zhixing，Yin Xuejian
（School of Mathematical Sciences，Anhui University，Hefei 230039，China）

In this paper，stable properties of one-legθ-methods for second-order delay differential equations is considered.It is proved numerical methods preserve corresponding stability of this system ifθ＝1.

second-order delay differential equation；stability；one-legθ-methods

O241.81

A

1673-1794（2011）05-0013-02

陈志兴（1981－），男，硕士研究生，研究方向：微分方程与动力系统；殷雪剑（1984－），女，硕士研究生，研究方向：微分方程与动力系统。

2011-04-15