大学数学学习中的“知其所以然”

谢如龙 戴泽俭 陈侃

（巢湖学院数学系，安徽 巢湖 238000）

大学数学学习中的“知其所以然”

谢如龙 戴泽俭 陈侃

（巢湖学院数学系，安徽 巢湖 238000）

在学习大学数学的过程中，很多学生只知道套用某种方法解决问题或者硬记一些结论，即知其然，但是并不知这种方法的深层次含义，也不知这些结论成立的背景，即并不知其所以然。本文通过几个例题来说明一些数学方法的深层次含义和某些结论成立的背景。

大学数学学习；知其所以然；方法

很多学生在解决大学数学问题时总是按照固定的模式去套用公式或方法，但并不知这样做的理由，只知道硬记一些结论，但不知这些定理成立的实际背景，这种学习数学的方法是机械的，致使知识掌握不牢，也不能应用知识灵活解决问题，所以要强调在学习过程中“知其所以然”，不仅要知道如何去解决问题，还要知道这样处理的理由.不仅要知道定理的结论，还要思考结论成立的实际背景.只有这样，才能做到融汇贯通，举一反三，真正的学好大学数学.下面通过几个不同数学学科的例题来说明一些数学方法的深层次涵义和某些结论成立的实际背景.

例1利用高斯公式计算

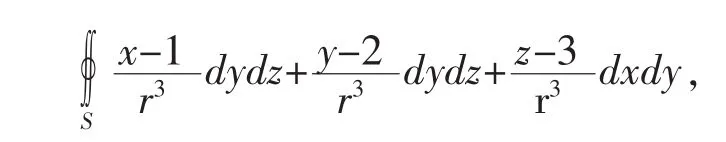
不少学生做法如下：

解 由于

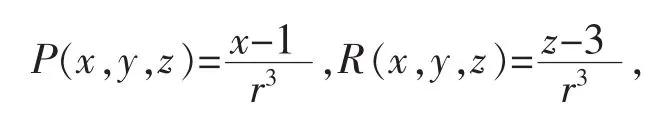
所以

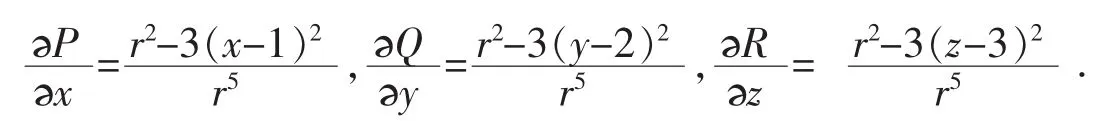
于是由高斯公式得

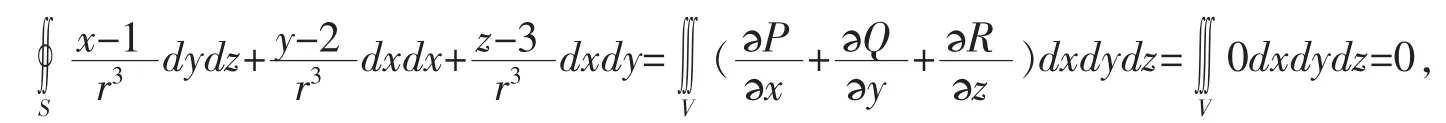
其中V为S所围成的空间区域.

上述做法是错误的，高斯公式的内容如下：

定理1[1]设空间区域V由分片光滑的双侧封闭曲面S围成，若函数P，Q，R在V上连续，且有一阶连续偏导数，则

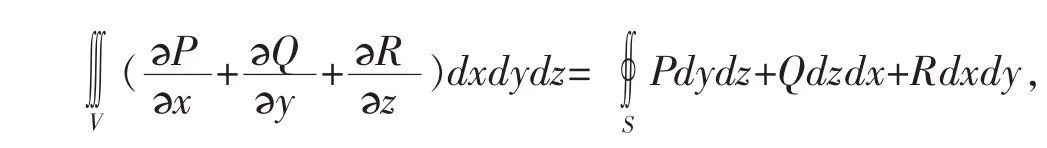
其中S取外侧.

这种做法错误的原因是函数P，Q，R在S内部的点 （1，2，3）处无定义且不是可去间断点，也不在此点连续，故不能直接使用高斯公式.

正确解法如下：

解 在S上r=1，先化简后再使用高斯公式，得

得B的全部特征值为-2，x，1.

因为相似的矩阵有相同的特征值（包括重数），而A与B相似，故他们的特征值全部相同，于是得x=-2.

事实上，以上的做法是错误的，错误的原因就是没有认清到充分条件与必要条件的关系.有相同的特征值只是矩阵相似的必要条件而非充分条件[2].若将x=-2代入B，得对角矩阵.而对A的二重特征值

故A不能对角化，即A不能与对角矩阵B相似，所以x=-2不符合条件，因此本题满足条件的x不存在.

在解题时，一定要弄清楚充分条件与必要条件的关系，否则就会出现多解或漏解.

很多学生都能写出sin2z+cos2z=1（z为复数），却不知为何跟实数域中的结论完全相同，这是因为在《复变函数》中有如下的解析函数的唯一性定理.

定理2[3]设在区域D内解析的函数f1（z），f2（z）在D内的某一子区域（或一小段弧）上相等，则它们在区域D内恒等.

故一切在实轴上成立的恒等式在复平面上同样成立，只要恒等式的等号两边在复平面上都是解析的，这也是很多函数在复数域中的Taylor展式与实数域中的Taylor展式结构相同的原因.

实际上，通过复变函数的学习，我们还知道收敛半径的另一层涵义.

设f（z）在点a解析，b是f（z）的奇点中距a最近的一个奇点，则的幂级数的收敛半径.

例5 在《数学分析》中学习的柯西收敛准则在任何情况下都能判断收敛性吗？

学生们在学习《数学分析》课程中接触到了柯西收敛准则，就以为在任何情况下都能用它来判断收敛性，这是错误的理解.在《数学分析》中可以大胆运用柯西收敛准则是因为Rn本身是一个完备度量空间的缘故，在《泛函分析》中，给出了完备度量空间的涵义.

如果度量空间（X，d）中的每个柯西点列都在（X，d）中收敛，则称（X，d）是完备的度量空间[4].

实际上，收敛点列一定是柯西点列，但柯西点列并不一定是收敛的，只有在完备空间的基础上两者才等价，也只有在完备的前提下才会有柯西收敛准则，也有利于理解在《数学分析》中柯西收敛准则是实数的完备性的性质之一，同样，因为全体复数形成的空间是完备空间，所以也有柯西收敛准则和复数的完备性.

不少学生做法如下：

解 因为

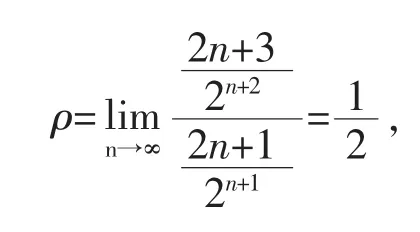
所以收敛半径R=2.

上述做法的思路来源于下面的定理.

定理3[1]对于幂级数若

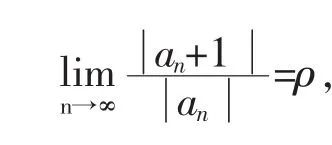
则当

（ii） ρ=0时，原幂级数的收敛半径 R=+∞；

（iii）ρ=+∞时，原幂级数的收敛半径R=0.

值得一提的是，定理3是对不缺项的幂级数求收敛半径有效，对于缺项的情况就不能再用这个定理来求解，所以例6按定理3方法来求解是错误的，正确的做法如下：

解 由于

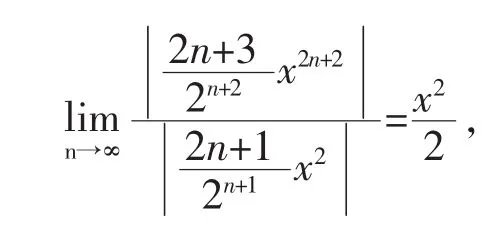
例7甲、乙两人独立地对同一目标射击一次，其命中率分别为0.6和0.5，现已知目标被击中，求它被甲射中的概率.

不少学生有如下解法：

解 令A=｛目标被击中｝，B｛甲命中目标｝，C=｛乙命中目标｝，于是由贝叶斯公式得

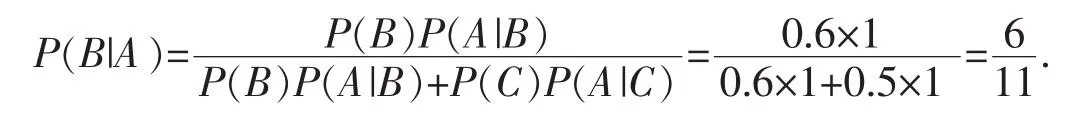
以上解法看起来正确，但实际上，在本题中事件B/C并不构成完备事件组，故不能硬搬贝叶斯公式，正确解法应该是：

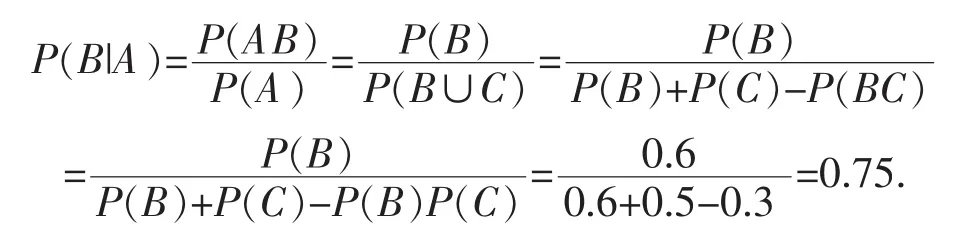
通过以上例题的学习，启发我们要想在数学学习中“知其所以然”，就必须要从两个方面下功夫，一要勤于思考，平时遇到一个数学问题，不能解答完就丢在一边，要多问几个为什么，考虑这种解法的深层次涵义和结论成立的各种条件；二要拓宽数学知识面，很多当时疑惑的问题就会在进一步的学习或者在新的课程的学习中得到解决，并对当初的问题有更深更全面的理解.

[1]华东师范大学数学系.数学分析(第三版)[M].北京：高等教育出版社，2001.

[2]北京大学数学系几何与代数教研室前代数小组.高等代数(第三版)[M].北京：高等教育出版社，2003.

[3]钟玉泉.复变函数论(第三版)[M].北京：高等教育出版社，2003.

[4]程其襄，张奠宙，魏国强，胡善文，王潄石.实变函数与泛函分析基础(第二版)[M].北京：高等教育出版社，2003.

[5]魏宗舒.概率论与数理统计教程[M].北京：高等教育出版社，1983.

TALKING WITH “KNOWING THE REAL REASONS”IN COLLEGE MATHEMATICAL LEARNING

XIE Ru-long DAI Ze-jian CHEN Kan
(Department of Mathematics,Chaohu University,Chaohu Anhui 238000)

In the process of studying college mathematics,many students only know solving problems by simulating some methods or remembering some results,but not know the real meaning of this method and the background of results.In this paper,we interpret the real meaning of some method and the background of results by giving some examples.

college mathematical learning;knowing the real reasons;methods

G420 < class="emphasis_bold">文献标识符：

符：A

1672－2868（2011）03－0128－04

2010-11-16

巢湖学院院级重点课程（高等数学）；安徽省教研项目（项目编号：2008jyxm438）

谢如龙（1982-），男，安徽怀宁人。讲师，硕士，研究方向：调和分析

责任编辑：陈 凤