局部n次积分C-半群与抽象Cauchy问题

秦喜梅

（巢湖学院，安徽 巢湖 238000）

局部n次积分C-半群与抽象Cauchy问题

秦喜梅

（巢湖学院，安徽 巢湖 238000）

在局部n次积分C-半群的概念和性质的基础上,给出了局部n次积分C-半群在抽象Cauchy问题上的应用.

局部n次积分C-半群；生成元；抽象Cauchy问题

1 引言

作为C0半群的推广，1987年Arent提出的积分半群，Davies和Pang提出的C-半群为算子半群的发展注入了新鲜血液，给出了算子半群的更一般的框架，解决了一些强连续算子半群不能处理的不适定Cauchy问题，得到了许多重要的微分方程在某种弱意义下的适定性.本文就局部的n次积分C-半群，讨论了它们与抽象Cauchy问题的联系，丰富了抽象Cauchy问题的研究内容.

以下均假设X为一Banach空间，所涉及的算子均为线性算子.C∈B（X），其中B（X）为X上所有有界线性算子的集合。n∈N，T∈（0，∞].

2 基本概念和性质

定义1 强连续算子族｛S（t）}0≤t＜T⊂B（X）称为局部 n 次积分 C-半群如果满足：

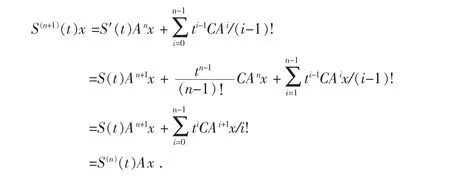
2 主要结论

[1]Arendt W.,Vector-valued Laplace Transforms and Cauchy Problem[J].Israel J.Math.,1987，（59）:327-352.

[2]Ralph Delaubenfels,Semigroups and the Cauchy Problem[J].Journal of Functional Analysis,1993,111（1）:44-61.

[3]Zheng Quan,Perturbations and Approximations of Integrated Semigroups[J].Acta Math.Sinica,1993，9（3）:252-260

[4]Wang ShengWang,Mild Integrated existence Families[J].Studia Math.,1995，112（3）:251-266.

[5]孙国正.-次积分 半群与抽象柯西问题[J].Acta Math.Sinica,1999，42（4）:757-762.

[6]赵华新，刘清荣，局部积分 半群与抽象柯西问题（Ⅲ）[J].纯粹数学与应用数学，1996，12（1）:53-58.

LOCAL N TIMES INTEGRATED C-SEMIGROUPS AND THE ABSTRACT CAUCHY PROBLEM

QIN Xi-mei
（Chaohu College,Chaohu Anhui 238000）

This paper presents several characterizations of a local n times integrated C-semigroups.We discuss the solutions of the associated abstract Cauchy problem.

local n times integrated C-semigroups； generator； abstract Cauchy problem

O177

A

1672－2868（2011）03－0013－04

2010-09-26

安徽省教育厅自然科学研究项目（项目编号：KJ2010B127）和（项目编号：KJ2009B097）

秦喜梅（1982-），女，安徽阜阳人。巢湖学院数学系教师，研究方向：算子半群及其应用

责任编辑：陈 侃