带有变指标反应项的非线性抛物方程解的爆破

唐树乔，郭 彦

(1.东南大学 数学系，南京 211100;2.亳州师范高等专科学校 理化系，安徽 亳州 236800;3.南京财经大学 应用数学学院，南京 210046)

带有变指标反应项的非线性抛物方程解的爆破

唐树乔1，2，郭 彦1，3

(1.东南大学 数学系，南京 211100;2.亳州师范高等专科学校 理化系，安徽 亳州 236800;3.南京财经大学 应用数学学院，南京 210046)

通过引入特征函数和构造适当的上解，讨论了一类带有变指标反应项的非线性抛物方程的爆破行为，并证明了这类方程初边值问题的非负解在有限时刻爆破和整体存在。

非线性抛物方程;特征函数方法;整体存在;爆破

0 引言

本文考虑下列带有变指标反应项的非线性抛物问题

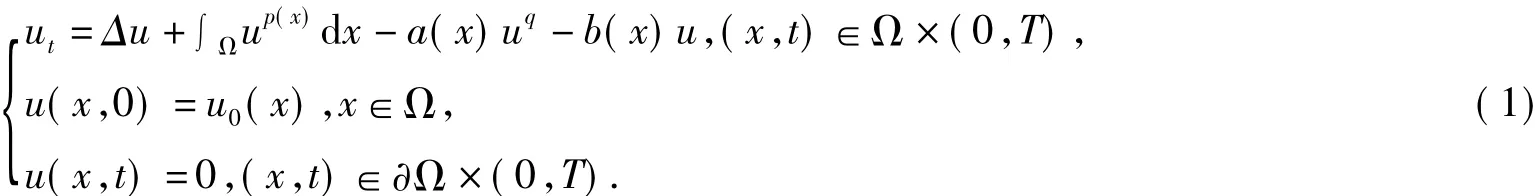
其中Ω⊂RN是带有光滑边界∂Ω的有界区域，q＞1，初值u0(x)是非平凡的非负连续有界函数。而连续函数p(x)、a(x)、b(x)则满足以下条件:

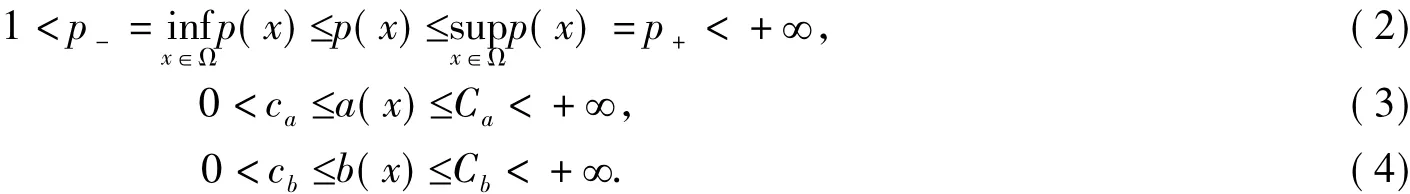
几十年来，人们对非线性抛物方程ut=Δu+f(u)解的爆破问题进行了大量深入的研究，如参考文献［1－3］。然而带有变指标反应项的非线性抛物方程解的爆破现象，却是近几年才开始步入人们的视野，已发表的论文也不多，有兴趣的读者不妨查阅下文后所列的参考文献［4－9］。

定义1.1如果存在常数 T(0＜T＜∞)，使得方程(1)的解 u(x，t)在上存在，并且有，那么称方程(1)的解u(x，t)在有限时刻T爆破，时间T称为爆破时间。

定义1.2如果方程(1)的解u(x，t)在上存在，那么称方程的解u(x，t)整体存在。

引理1.1设η(t)为连续可导函数且满足不等式:

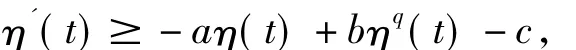
其中常数 q＞1，a，b，c＞0。若 η(0) ＞0，－aη(0)+bηq(0) －c＞0，则 η(t)爆破。证明:取

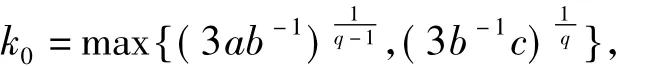
只要 η(0)≥k0，就有在［0，T)上积分并注意到 q＞1，有，从而η(t)爆破。

1 解的爆破

对于方程(1)的解的爆破性质，我们有如下定理:

定理2.1设Ω⊂RN是带有光滑边界∂Ω的有界区域，初值u0(x)是非平凡的非负连续有界函数，连续函数p(x)、a(x)、b(x)满足条件(2)－(4)，那么当p－＞q＞1时，对于充分大的初值u0(x)，方程(1)的非负解u(x，t)在有限时刻爆破。

由带权的 Höld不等式［10］，我们可以推知

于是当方程(1)的初值u0(x)充分大时，即y(0)=∫Ωu0(x)w(x)dx充分大时，由引理1.1即可推知方程(1)的解在有限时刻爆破。

2 解的整体存在

对于方程(1)的解的整体存在性质我们给出以下结论:

定理3.1设Ω⊂RN是带有光滑边界∂Ω的有界区域，q＞1，初值u0(x)是非平凡的非负连续有界函数，连续函数p(x)、a(x)、b(x)满足条件(2)－(4)，那么当p(x)≤1时，方程(1)的非负解u(x，t)对任意初值整体存在。

证明:当p(x)≤1时，构造函数

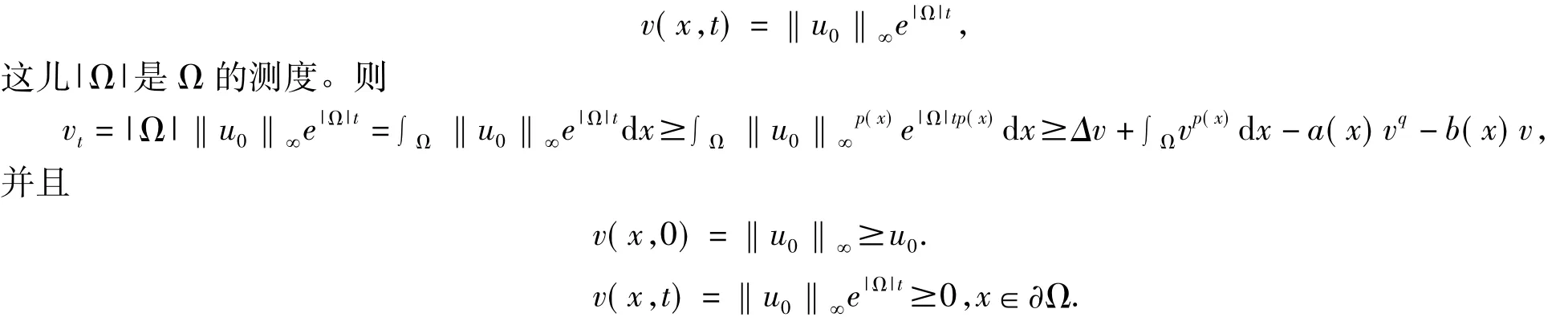
从而v(t)为方程(1)的上解，所以方程(1)的非负解对任意初值整体存在。

［1］ Fujita H.On the blowing up solutions of thecauchy problem for ut= Δu+u1+α［J］.J.Fac.Sci.Univ.Tokyo.Sect.A.Math，1996(16):105 －113.

［2］ Weier P.On the critical exponent for reaction—diffusion equations［J］.Arch.Rational Mech，1990(109):63 －71.

［3］ Liu，Qilin;Li，Yuxiang;Gao，Hongjun.Uniform blow－up rate for a nonlocal degenerate parabolic equations［J］.Nonlinear Anal，2007(66):881－889.

［4］ S.N.Antontsev，S.I.Shmarev，Existence and uniqueness of solutions of degenerate parabolic equations with variable exponents of nonlinearity［J］.J.Math.Sci，2008(150):2289 －2301.

［5］ S.N.Antontsev，S.I.Shmarev，A model porous medium equation with variable exponent nonlinearity:existence，uniqueness and localization properties of solutions［J］.Nonlinear Anal，2005(60):515 － 545.

［6］ J.P.Pinasco.Blow－up for parabolic and hyperbolic problems with variable exponents［J］.Nonlinear Anal，2009(71):1094 － 1099.

［7］ Xueli Bai and Sining Zheng.A semilinear parabolic system with coupling variable exponents［J］.Annali di Mathematic Pura ed Application，2011，190(3):525－537

［8］ Ferreira，R.，de Pablo，A.，Pérez－Llanos，M.，Rossi，J.D.Critical exponents for a semilinear parabolic equation with variable reaction［J］.preprint.

［9］ 刘云霞.带有变指标反应项的半线性抛物方程的临界指标［D］.大连:大连理工大学，2009.

［10］ 王术.Sobolev空间与偏微分方程引论［M］.北京:科学出版社，2009:18－19.

Blow-up of Solutions to Nonlinear Parabolic Equations with Variable Exponents

TANG Shu－qiao1，2，GUO Yan1，3

(1.Department of Mathematics，Southeast China University，Nanjing 211100，China;2.Department of Science，Bozhou Teachers College，Bozhou 236800，China;3.Applied Mathematics Institute，Nanjing University of Finance and Economics，Nanjing 210046，China)

Through introducing characteristic function and constructing proper upper solutions，this paper discusses the blow－up of a class of nonlinear parabolic equations with variable exponents and proves the blow－up and global existence of the nonnegative solutions to the initial boundary problems.

nonlinear parabolic equation;characteristic function method;global existence;blow－up

O175.26

A

1009－3907(2011)12－0068－02

2011－09－24

安徽省自然科学基金(KJ2011Z258);亳州师范高等专科学校数学教育专业(省级特色专业);江苏省基础研究计划自然科学基金项目(BK2010404)

唐树乔(1973－)，男，安徽蒙城人，讲师，硕士，主要从事非线性偏微分方程(组)理论及其应用方面的研究。

责任编辑:钟 声