具有放养率的时滞捕食模型的分岔行为

李石涛

具有放养率的时滞捕食模型的分岔行为

李石涛

(沈阳工业大学 基础部，辽宁 辽阳 111000)

考虑一类具有常数放养率的时滞捕食种群模型，研究了种群稳定性和分岔行为。通过对特征方程的研究，得到种群稳定及发生分岔行为的充分条件;利用MATLAB软件进行数值模拟，给出相空间的轨迹，得到时滞与放养率是影响种群稳定的两个重要因素，验证了理论分析所得结果的正确性。

时滞;放养率;稳定性;分岔

0 引言

可更新资源的持续开发和利用，已成为经济管理学家和生态学家都在关心的问题之一，而时滞对生物种群的动力学行为的影响也得到生物学家的关注［1，2，3］。许多学者研究了具有开发的时滞的捕食—被捕食种群模型，关于可持续开发给出研究结果［4，5，6］。已有的大部分工作集中在不含放养项的捕食—被捕食系统，对模型的分岔点及正平衡点稳定的充分条件给出了一些研究结果［7，8］。本文考虑了具有常数放养率的时滞功能性捕食模型如下

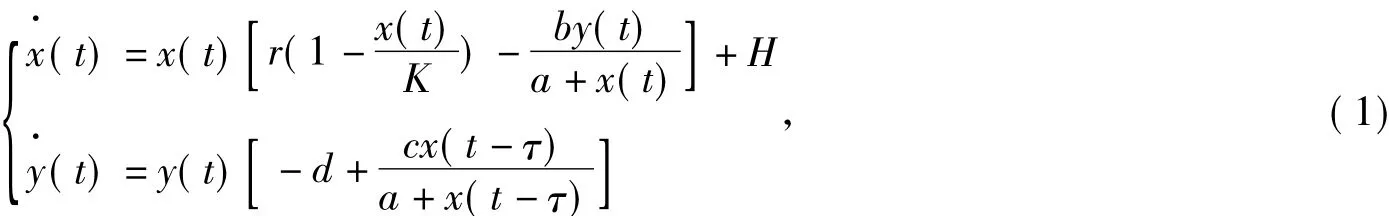
其中x(t)，y(t)分别代表被捕食者，捕食者种群密度;r为被捕食者出生率;K为最大容纳量;d为捕食者死亡率;τ为时滞量;H为被捕食者的常数放养率;为捕食者种群的Holling II型功能性反应函数;a，b，c，d，r，k，H 皆为正数。

1 主要结论

设 E*(x*，y*)为模型(1)的平衡点，即(x*，y*)满足

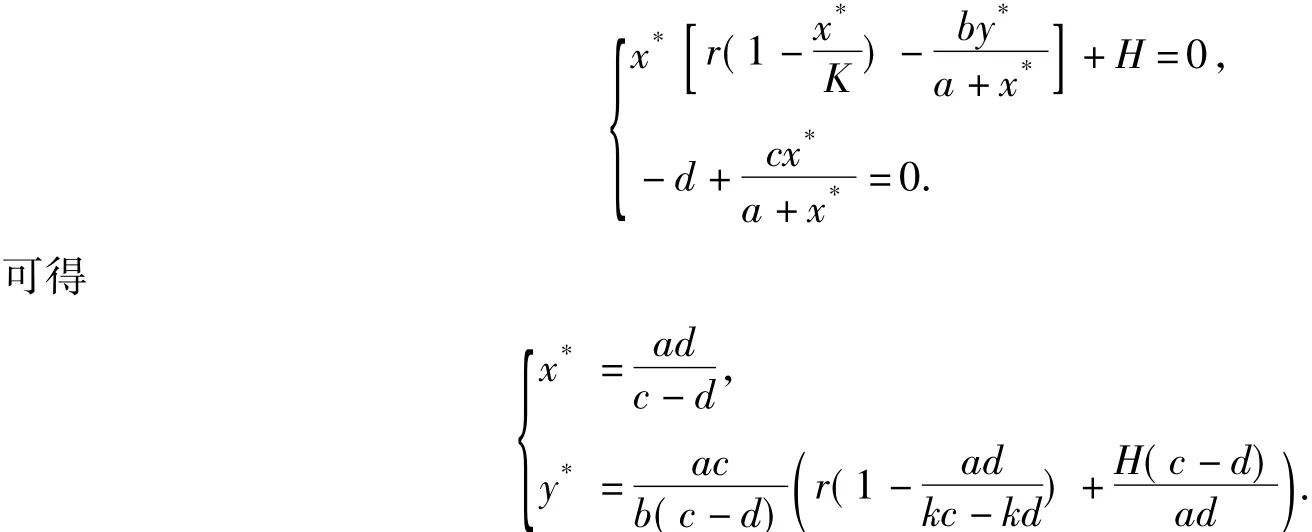
定理1若模型(1)满足则存在正平衡点E*(x*，y*)。

模型(1)在正平衡点E*(x*，y*)处线性化，对应的系数矩阵的特征方程为

从上面的分析，可得

为了研究分岔发生的充分条件，对方程(3)的两边同时求导，可得

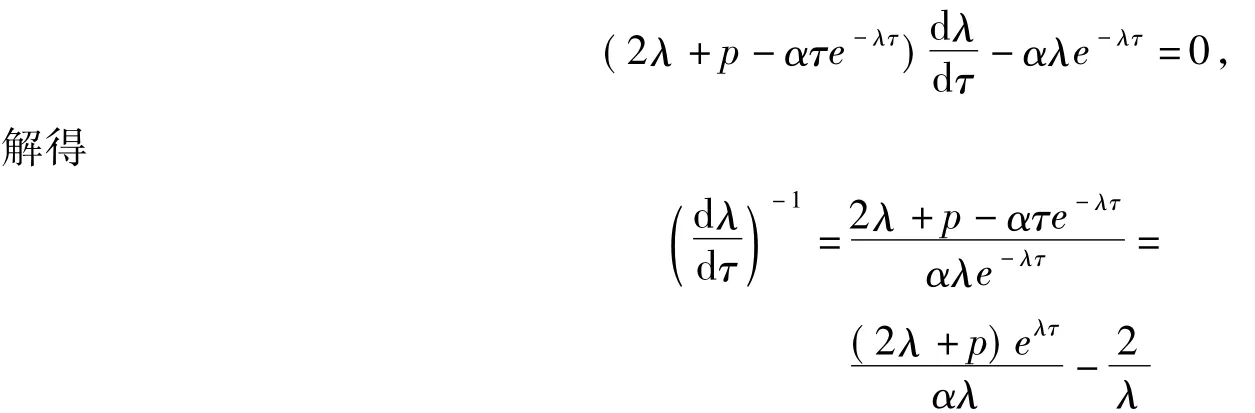
令ω0是与(k=0)对应的纯虚根，即，由此可计算

定理3设E*(x*，y*)为模型(1)的正平衡点，若时，E*(x*，y*)是渐近稳定;当时，E*(x*，y*)是不稳定的;当时，模型(1)发生分岔。

2 数值模拟

为了验证所得结论的正确性以及时滞和放养率的改变对稳定性的影响，采用数值模拟的方法给出相空间的相轨迹，更好的揭示种群的变化趋势。

在模型(1)中取 r=1，K=100，a=60，b=1，c=4，d=2，H=10，通过定理 2 可得正平衡点(x*，y*)=(60，68)，p=0.4833=0.9098，可知时滞 τ＜0.9098 时，有渐进稳定的平衡点;τ＞0.9098 时，有不稳定的平衡点;下面使用Matlab进行数值模拟，分别给出τ=0.90及τ=0.93时的相轨迹。

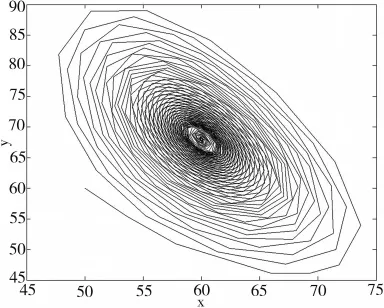
图1 当 τ=0.90，H=10时模型(1)的相图

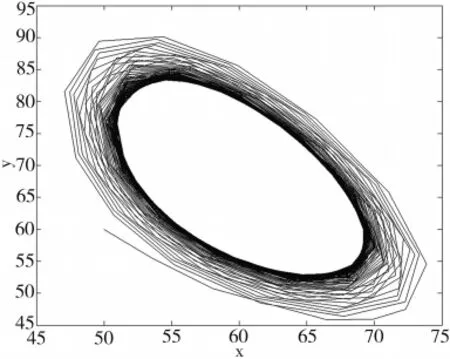
图2 当 τ=0.93，H=10时模型(1)的相图

从图中可以清楚的看出，当τ=0.90时，平衡点渐近稳定，相轨迹最终进入相平面的有界区域并趋近于正平衡点。当τ=0.93时，出现一个分岔周期解，种群的数量进行周期性振荡。这种情况表明时滞的微小变化对稳定性有着重要影响。

为了更好的理解放养对种群稳定性的影响，在保持时滞不变的情况下，可以看到放养率的改变同样影响平衡点的稳定性。如图3、图4所示:

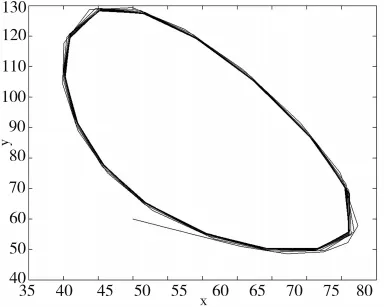
图3 当 τ=0.90，H=20时模型(1)的相图

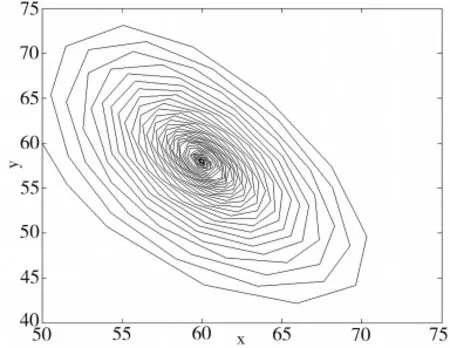
图4 当 τ=0.93，H=5时模型(1)的相图

通过对图1、图3的比较，可以得出在时滞不变的情况下，放养率的增加改变了平衡点的稳定性，对应自然界的两种群，在增加放养的同时，使得被捕食者数量显著增加，改变了捕食者与被捕食者的种群数量的平衡，进而出现种群的周期性振荡现象。从图2与图4可以得出，放养率的减少使得原本周期震荡的种群数量稳定于一个具体的数值，对应自然界的两种群，在放养减少的情况下，捕食者对被捕食者种群数量的影响成为主要因素，最终两种群数量趋于稳定状态。

［1］ 滕勇，李石涛.一类具有时滞的捕食－被捕食模型的持久性［J］.吉林大学学报，2011，49(3):478－480.

［2］ 李石涛，李冬梅.一类具有时滞的捕食模型的持久性和稳定性［J］.沈阳工业大学学报，2008，30(6):687－692.

［3］ 李石涛，李冬梅.一类具有时滞的捕食模型的全局稳定性［J］.沈阳理工大学学报，2008，27(5):91－94.

［4］ Annik Martin，Shigui Ruan.Predator-Prey models with delay and prey harvesting［J］.Mathematical Biology，2001(43):247 －267.

［5］ 李石涛，许爽爽.具有时滞和常数收获率种群模型的稳定性［J］.高师理科学刊，2004，19(1):87－92.

［6］ Cook，K.L.，Grossman，Z.Discrete delay，distributed delay and stability switches［J］.J.Math.Anal.Appl.，1982(86):592 －627.

［7］ Chen Fengde.The Permanence and Global Attractivity of Lotka-Volterra Competition System with Feedback Controls［J］.Nonlinear Analysis Real World Applications，2006，7(1):133 －143.

［8］ 杨建雅，张凤琴.一类具时滞的捕食－被捕食系统的稳定性与Hopf分支［J］.数学的认识与实践，2010，40(18):163－167.

Bifurcation Behavior of the Breeding Rate-based Predator-prey Model with Time Delays

LI Shi-tao

(Department of Basic Courses，Shenyang University of Technology，Liaoyang 111000，China)

This paper considers a class of predator-prey species model with time delay which has the constant breeding rate and studies the stability and bifurcation of the species.Sufficient condition for stability and bifurcation is obtained by studying the characteristic equation.The numerical simulation is carried out by using Matlab software and the trace of phase space is obtained.It comes to a conclusion that time delay and stocking rate are the two factors effecting stability of species，which verifies the correctness of the theoretical analysis result.

time delay;stocking rate;stability;bifurcation

O175

A

1009－3907(2011)12－0060－04

2011-09-16

黑龙江省自然基金资助项目(A200502);黑龙江省教育厅资助项目(10051061)

李石涛(1978-)，男，辽宁辽阳人，讲师，主要从事微分方程、生物数学的研究。

责任编辑:钟 声