80°后掠三角翼强迫俯仰、自由滚转双自由度耦合运动特性数值研究

杨小亮，刘伟，赵云飞，刘 君

(国防科学技术大学航天与材料工程学院宇航科学与工程系，湖南 长沙 410073)

0 引言

战斗机大攻角条件下的动态运动特性，一直是国内外学者研究的热点之一，近几十年来开展的大量研究主要采用了以下两类思路:一类是不考虑滚转运动的单自由度快速上仰或是强迫俯仰振动，另一类是不考虑动态俯仰角影响的单自由度自激摇滚。一般认为，快速上仰运动能够推迟战斗机的失速攻角和提高战斗机的最大升力系数［1］(如Su-27战斗机的眼镜蛇机动Cobra Maneuver)，国外 Hoang［2］，Visbal［3］等以及国内的白涛［4］、杨立芝［5］等都针对三角翼的俯仰运动进行了研究。而在单自由度摇滚方面，Nguyen等1981年的一篇报告［6］，被公认是对三角翼自激摇滚问题最早的实验研究，后来，Kandil领导的研究小组完成了三角翼自激摇滚的数值模拟［7］，在国内，杨希明［8］、唐敏中［9］等人采用实验的方法研究了三角翼的自激摇滚，刘伟［10］研究了细长机翼自激摇滚的数值模拟方法，张涵信［11］从非线性动力学的观点给出了细长机翼产生自激摇滚的解析条件。然而真实的战斗机上仰机动飞行，往往导致横向失稳，发生非可控的自激滚转，形成俯仰、滚转耦合的运动，纵横向运动交感耦合和运动学关联效应将会导致气动力/力矩的强非线性，使得战斗机操稳性能下降，危及飞行安全。目前，采用实验方法针对俯仰、滚转耦合运动的研究［12］还不多，而对三角翼俯仰、滚转双自由度耦合运动的数值研究也仅仅局限于给定强迫俯仰、强迫滚转运动条件下的模拟［13］，这样的纯强迫运动虽然能够从一定程度上反映战斗机气动力/力矩的迟滞特性，但对纵横向运动交感耦合的模拟有其无法回避的局限性。

本文耦合求解Navier-Stokes方程和俯仰/滚转运动方程研究80°三角翼在强迫俯仰、自由滚转双自由度条件下的运动特性，得到了与试验定性相符的结果，分析了俯仰/滚转双自由度耦合运动与单自由度滚转及俯仰运动的差异，研究了多自由度耦合运动条件下自激滚转运动产生的机理，给出了俯仰/滚转耦合运动条件下三角翼的气动力/力矩特性。

1 模型及数值方法

1.1 三角翼模型

本文计算使用的80°后掠三角翼模型如图1所示，模型的前缘及尾缘采用单面削尖处理。文献［14］通过计算比较，认为H型网格在模拟的准确性上具有优势，O型网格能够有效地节省周向网格，因此本文采用周向O型、其余方向H型的OH型网格进行计算，翼面网格分布如图1所示。

图1 80°后掠三角翼模型Fig.1 80°delta wing model

1.2 控制方程

机翼的强迫俯仰运动给定正弦规律:

假定俯仰轴、滚转轴均为惯量主轴，则三角翼滚转运动方程为:

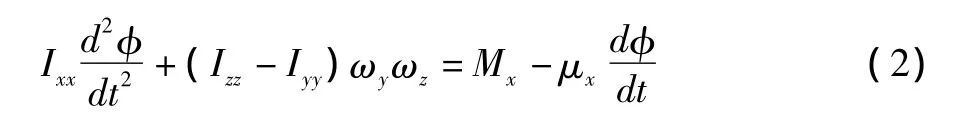
无量纲化(2)式并进行简化得:

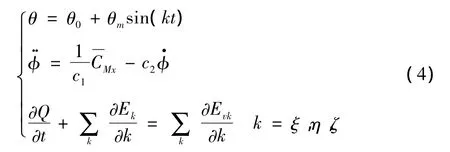
其中Q为守恒变量，Ek、Evk分别为对流通量和粘性通量，ξ、η、ζ为贴体坐标系坐标。

1.3 数值离散方法

采用空间二阶NND格式和含双时间步法的LUSGS方法有限体积离散NS方程。刚体滚转运动方程采用时间二阶精度的单边差分离散、，得到时间二阶精度的差分方程:

采用松耦合的方式联立求解流动控制方程和刚体动力学方程，即由刚体动力学方程提供三角翼“n+1”时刻的位置，再由流动控制方程计算“n+1”时刻的滚转力矩系数。

计算域远场采用无反射边界条件，壁面边界取绝热壁假设，压力条件为:，速度条件为考虑物面双自由度运动的无滑移条件:

2 三角翼单自由度自激滚转数值模拟

一些文献完成了80°后掠三角翼单自由度自激滚转的实验［8，9，15］和数值计算［10］，但由于模型的差异以及与实验条件不能完全一致，如前缘形状、模型厚度、来流马赫数、雷诺数等，特别是不同轴承摩擦阻尼的差异，导致研究得到的自激滚转角振幅、频率有一定差别，但定性结论基本一致。

本文首先计算了80°后掠三角翼的单自由度自激滚转，根弦名义攻角30°，来流马赫数Ma=0.35，根弦雷诺数 Re=1.0 ×106，无量纲转动惯量 c1=0.65，不计机械阻尼，所得运动特性如图2所示。振幅从0°逐渐增大，形成以0°为平均滚转角、振幅38°左右极限环形式荡，曲线振幅、频率稳定，与相关文献的研究结果［10，15］定性相符。

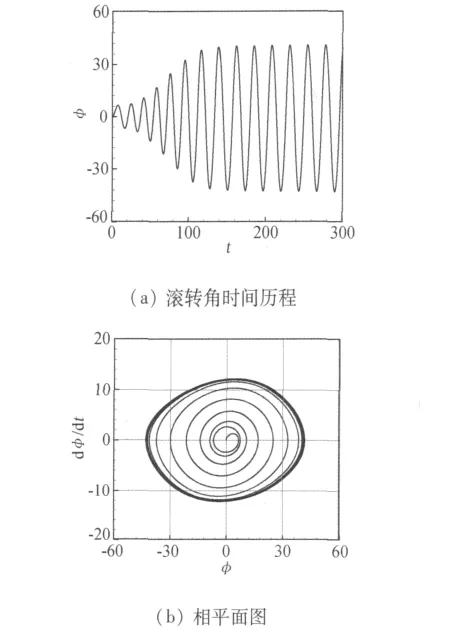
图2 单自由度自由滚转运动特性Fig.2 Characteristics of self-excited roll motion的 振

3 三角翼强迫俯仰、自由滚转双自由度运动数值研究

对80°后掠三角翼强迫俯仰、自由滚转耦合运动的模拟采用图1所示的网格，给定来流 Ma=0.35，Re=1.0 ×106，俯仰减缩频率 k=0.005，研究俯仰角在 0°～40°之间以正弦规律运动时的自激滚转特性。给定无量纲转动惯量c1=0.65，机构阻尼c2=0，初始俯仰角θ0=20°，俯仰振幅 θm=20°，以及 0°初始滚转角，模拟得到80°后掠三角翼强迫俯仰、自由滚转双自由度耦合运动的姿态角时间历程如图3所示。在动态俯仰角θ的影响下，滚转角时间历程曲线的振幅和频率也随之发生变化，大致呈现为:在俯仰运动的正行程(＞0)，由于攻角总体增大，自由滚转的振幅增大、频率加快;在俯仰运动的负行程(＜0)，由于攻角总体减小，自由滚转的振幅减小、频率变缓。与单自由度的自由滚转(如图2所示)比较发现，在双自由度运动达到最大滚转振幅时的频率与单自由度的自激摇滚频率相当，而在俯仰振动曲线的波谷区域，频率明显比单自由度自激滚转的频率低。在俯仰运动的正行程，机翼向上的速度分量导致等效攻角减小，延迟了涡破裂在翼面上发生;在俯仰运动的负行程，机翼向下的速度分量导致等效攻角增大，推迟了破裂涡流在翼面上的再附。

机翼俯仰运动速度对翼面上流动结构的形成具有延迟作用，导致最大振幅形成的位置滞后于最大俯仰角所在的位置(如图3所示)。唐敏中等人［12］采用实验的方法，研究了80°三角翼强迫俯仰、自由滚转的运动特性，给定来流速度30m/s，俯仰频率0.088Hz，折合无量纲俯仰减缩频率约为0.007，得到的运动特性如图4所示，其滚转振幅滞后于俯仰角变化的效应更为明显。图3(计算结果)显示了与图4(实验结果)定性一致的运动特性:随着俯仰角的变化，滚转角的振幅和频率经历了增大、稳定再减小的过程，滚转振幅总体随俯仰角的增大而增大，减小而减小。实验结果中值得注意的是，当俯仰角回到零附近的区域时，机翼运动到约－17°滚转角的位置突然停住，直至俯仰角再增大到5°左右时，又迅速起动向0°滚转角的位置运动，这可能和转动惯量、轴承摩擦阻尼以及翼面上的流态等因素有关，对该现象的进一步研究，作者另文阐述。

图3分别用A、B、C标识了80°后掠三角翼强迫俯仰、自由滚转耦合运动过程中俯仰运动第二周期中三个不同的滚转周期，分别代表振幅增大、振幅极值和振幅衰减时运动特性，其滚转力矩系数随滚转角的变化如图5所示。在周期A的过程中(曲线A)，曲线呈顺时针变化，说明机翼滚转从流动中汲取能量，因此振幅增大;在周期B的过程中(曲线B)，双“8”字型曲线中部的内环呈顺时针变化，表征机翼从流动中汲取能量，在曲线两端的外环呈逆时针变化，表征机翼滚转向流动释放能量，两部分面积大致相当，说明机翼在滚转振幅极值附近机翼与流动的能量交换大致平衡;在周期C的过程中(曲线C)，曲线呈逆时针变化，机翼滚转向流动释放能量，振幅衰减。

图6(a)、(b)分别是通过数值模拟和实验［12］得到的三角翼强迫俯仰、自由滚转双自由度耦合运动中滚转角的相平面图。计算的结果和文献［12］通过实验得到的结果定性一致，图中纵横交叉的相曲线显示了三角翼双自由度运动时，动态俯仰角对三角翼自由滚转运动特性的影响。

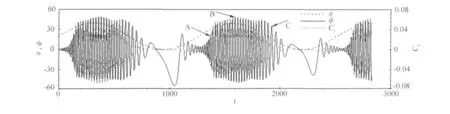
图3 强迫俯仰、自由滚转姿态角及滚转力矩系数时间历程Fig.3 Attitude angles and roll-moment coefficient vs.time in force-pitch and free-roll

图7 俯仰/滚转运动的气动力特性Fig.7 Aerodynamic characteristics of pitch/roll motion

三角翼自激滚转运动的形成和维持主要受到滚转力矩的影响，80°后掠三角翼强迫俯仰、自由滚转运动的滚转力矩系数如图3所示:起振的阶段滚转角在与其同号的滚转力矩的作用下逐渐增大;在振幅相对稳定的阶段，滚转力矩系数基本维持与机翼的自由滚转同频率的振荡;当俯仰角减小以后，由于俯仰角减小导致等效攻角显著减小，流动提供的滚转力矩不足以维持机翼极限环形式的振荡，振幅便开始减小;随着俯仰角的进一步减小，当俯仰角趋近零时，由于等效攻角减小，滚转力矩系数也趋于零，因此机翼在滚转方向几乎处于匀速滚转状态，滚转角缓慢转动到较大的角度;当俯仰角又从零开始逐渐增大，引起了等效攻角增大，使得起恢复作用的滚转力矩迅速变大，将机翼很快拉回到零滚转角附近，并进一步增大，进入了强迫俯仰运动下一周期的振荡，如此循环形成了80°三角翼强迫俯仰、自由滚转的周期性运动特性。

图7是80°后掠三角翼单自由度强迫俯仰气动力特性与俯仰/滚转耦合双自由度运动气动力特性的比较(曲线A是单自由度俯仰结果)。三角翼俯仰、滚转双自由度运动时，攻角的变化主要受俯仰角影响，如图7(a)所示，总体变化趋势是随俯仰角的增大而增大，减小而减小，而自由滚转运动的影响使得攻角减小，也就是说，攻角的变化是俯仰、滚转运动共同作用的结果。升力主要受攻角的影响，升力的变化总体和攻角的变化一致，因此俯仰运动的过程中伴随的滚转运动将会导致飞行器升力显著减小，如图7(b)所示，考虑自由滚转影响下的机翼俯仰运动，与单自由度俯仰运动相比，上仰引起平均失速攻角增大的幅度要小，能够达到的最大升力系数也要小，这对于机动飞行的安全具有重要影响，必须引起足够的重视。图7(c)、(d)分别是侧力和滚转力矩的变化，与单自由度的俯仰运动相比，俯仰滚转耦合运动产生了显著不等于零的侧力和滚转力矩，说明在滚转运动的影响下，机翼的横向稳定性变差，侧力的存在还会导致机翼的侧滑运动，应进一步研究。

4 结论

通过耦合求解NS方程和滚转运动方程研究了80°三角翼强迫俯仰、自由滚转双自由度运动特性，得到了与试验定性一致的结果，分析了双自由度耦合运动与单自由度滚转运动的差异以及一些运动现象产生的机理，并研究了双自由度耦合运动的气动力特性，得到了以下结论:

(1)机翼的俯仰运动速度对机翼自由滚转运动的振幅具有迟滞作用，使得滚转振幅的变化落后于俯仰角的变化;

(2)在动态俯仰角的影响下，三角翼的自由滚转不能形成极限环形式的自由滚转振荡，滚转运动的振幅大致随俯仰角的增大而增大，减小而减小;

(3)三角翼的俯仰、滚转双自由度耦合运动，在俯仰运动的波谷区域，起恢复作用的气动力矩较小，在不计轴承机械阻尼的情况下，机翼匀速滚转至较大滚转角的位置，与试验结果有明显差异，应进一步考虑转动惯量、轴承摩擦以及湍流等多种因素的影响;

(4)俯仰耦合滚转运动将导致升力显著降低，对机动飞行安全不利，同时俯仰、滚转运动的耦合导致机翼的横向稳定性变差，真实的机动飞行可能还耦合了包括侧滑在内的其他形式的运动，应进一步研究。

致 谢:张涵信院士对本文的工作提出了许多宝贵的建议，在此表示衷心的感谢。

［1］ERICSSON L E.Delta wing vortex dynamics in high rate oscillations in pitch［R］.AIAA paper 97－0327，1997.

［2］HOANG N T，REDINIOTIS O K，TELIONIS D P.3-D LDV measurements over a delta wing in pitch-up motion.［R］.AIAA paper 93－0185，1993.

［3］VISBAL M R.Computational study of vortex breakdown on a pitching delta wing［R］.AIAA paper 93 －2974，1993.

［4］白涛，吕志咏，杨晓峰.动态三角翼的非定常气动特性和压力分布相关研究［J］.流体力学实验与测量，2004，18(2):38－42.

［5］杨立芝，高正红.绕三角翼纵向俯仰大迎角气动特性计算研究［J］.航空学报，2003，24(5):413－416.

［6］NGUYEN L E，YIN L P，CHAMBERS J R.Self-induced wing rock of slender wings［R］.AIAA paper 81 － 1883，1981.

［7］KANDIL O A，MENZIES M A.Effective control of computationally simulated wing rock in subsonic flow［R］.AIAA paper 97－0831，1997.

［8］杨希明，程厚梅，张祖庚.大攻角80°前缘后掠平板三角翼摇滚实验与数值模拟［A］.空气动力学研究文集(第四卷)［C］.北京，1994，142 －148.

［9］唐敏中，王铁，张伟，徐忠利.低速三角翼滚摆试验研究［J］.空气动力学学报，1997，15(4):436 －443.

［10］刘伟.细长机翼摇滚机理的非线性动力学分析及数值模拟方法研究［D］.［博士学位论文］，国防科学技术大学研究生院，2004.

［11］张涵信，刘伟，谢昱飞，叶友达.后掠三角翼的摇滚及其动态演化问题［J］.空气动力学学报，2006，24(1):5 －9.

［12］唐敏中，张伟，何宏丽.俯仰、滚摆耦合复杂流场试验研究［J］.空气动力学学报，2001，19(1):47 －55.

［13］KANDIL O A，MENZIES M A.Coupled rolling and pitching oscillation effects on transonic shock-induced vortex-breakdown flow of a delta wing［R］.AIAA paper 96 －0828，1996.

［14］刘刚，周铸，黄勇，陈作斌.三角翼大迎角绕流数值模拟中网格的影响研究［J］.空气动力学学报，2004，22(4):481－485.

［15］ALAIN PELLETIER.A study of the nonlinear aerodyanmic characteristics of a slender double-delta wing in roll［D］.［Ph.D.thesis］.Notre Dame University，April 1998.