十进制数与二进制数之间的快速转换

孙继龙 桓美丽

（陕西工业职业技术学院，陕西 咸阳 712000）

十进制数与二进制数之间的快速转换

孙继龙 桓美丽

（陕西工业职业技术学院，陕西 咸阳 712000）

十进制数与二进制数之间的转换在《计算机应用基础》等课程中作为难点知识，对于初学者不易接受，传统方法又过于繁琐。本文提出一种简便的转换方法，取名为“8、4、2、1”位权标注法，学生易于理解、便于掌握，也有助于提高效率。

数制；转换；方法

数制也称计数值，是用一组固定的符号和统一的规则来表示数值的方法。

我们日常生活中接触的十进制数比较多。随着科学技术的发展，特别是电子计算机的发展，产生了二进制。

在工科类计算机及电子类专业中，很多课程都涉及到了数制的概念。数制是这些课程的基础内容。但对于初学者而言，很容易混淆。笔者根据多年的教学经验，总结出一种快速转换方法，即：“8、4、2、1”位权标注法。

一、进位计数制

（一）、十进制数

数码：由 0、1、2、3、4、5、6、7、8、9 十个不同的符号组成。位权：10n-1。

整数部分低四位的位权：103=1000，102=100，101=10，100=1，简称：千、百、十、一。

小数点后四位的位权：10-1=0.1，10-2=0.01，10-3=0.001，10-4=0.0001。

(5678.4321)10＝5×103＋6×102＋7×101＋8×100+4×10-1＋3×10-2＋2×10-3＋1×10-4=5678.4321

（二）、进制数

数码：由0、1两个不同的符号组成。

位权：2n-1。

整数部分低四位的位权：23=8，22=4，21=2，20=1，简称：8、4、2、1。

小数点后四位数的位权：2-1=0.5，2-2=0.25，2-3=0.125，2-4=0.0625。

二、传统方式的数制转换

（一）、二进制数转化为十进制数

由二进制数的一般表达式可知，只要将其按加权系数法展开，即可得到对应的十进制数。

【例1】将二进制数（1001.101）2转换成十进制数。（加权系数法）

解：

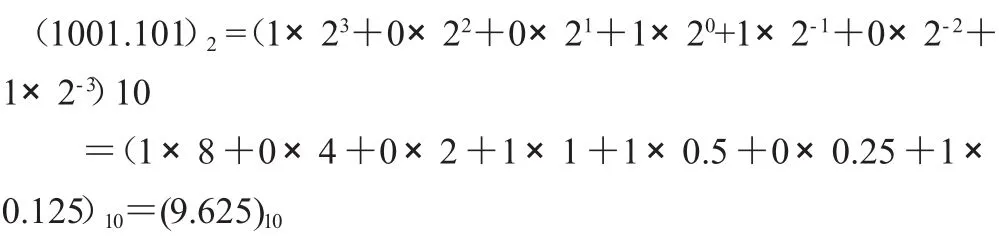
（二）、十进制数转换成二进制数

[1]整数部分的转换─—除2取余法，倒序排列

【例2】将十进制数(236)10转换成二进制数。

解：

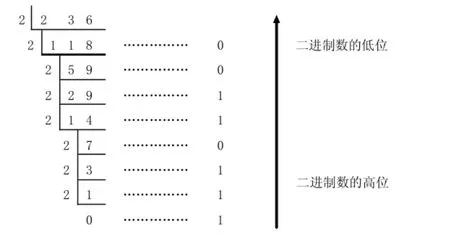
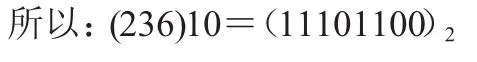
[2]小数部分的转换─—乘2取整法

【例3】将十进制纯小数0.562转换成保留六位小数的二进制小数。

解：

取整

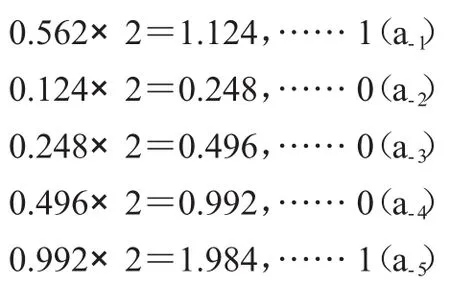
由于最后所余小数0.984〉0.5，则根据“四舍五入”的原则，可得（a-6）=1。

所以：（0.562）10≈（0.100011）2

三、快速转换方法

（一）、二进制数转化为十进制数

【例4】将二进制数（1111010010）2转换成对应的十进制数。

解：分析，如果仍然用加权系数法展开，列出的式子很长，比较繁琐且费时。我们不妨用下表列出各位数据上的位权，然后将“1”位上的位权相加，便很快地计算出正确结果。

首先，将原题抄写至表格的第二行。

其次，将整数部分低四位的位权8、4、2、1分别填入表格第一行的低四位。

再次，填写表格第一行其他位置上相应的位权，均为2倍的关系。先填写第五位上的位权16，再填写第六位上的位权32，依次类推……

最后，将表格第二行(二进制数)“1”位上的位权直接相加便得转换结果。

故（1111010010）2=512＋256＋128＋64＋16＋2=（978）10

【例5】将二进制数（0.01101）2转换成对应的十进制数。

解：首先，将原题抄写至表格的第二行。

其次，将小数点后四位数的位权 0.5、0.25、0.125、0.0626 分别填入表格第一行相应的位置。

再次，填写表格第一行其他位置上相应的位权，均为缩小二分之一的关系。

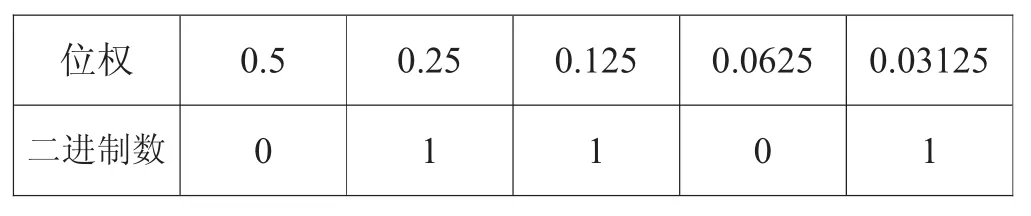
最后，将表格第二行(二进制数)“1”位上的位权直接相加便得运算结果。

故（0.01101）2=0.25＋0.125＋0.03125=（0.40625）10

（二）、十进制数转换成二进制数

【例6】将十进制数(234)10转换成二进制数。

解：首先，将整数部分低四位的位权8、4、2、1分别填入表格第一行的低四位。

其次，填写第五位上的位权16，第六位上的位权32，依次类推……直至满足题意。

再次，计算十进制数234中包含有哪些位权？并在相应位权的下面填写“1”。

234-128=106，在位权128的下面填写二进制数“1”；

106-64=42，在位权64的下面填写二进制数“1”；

42-32=10，在位权32的下面填写二进制数“1”；

10-8=2，在位权8的下面填写二进制数“1”；

2-2=0，在位权2的下面填写二进制数“1”；

二进制数其他空格里填写二进制数码“0”。

故 (234)10＝（11101010）2

【例7】将十进制数(0.8125)10转换成二进制数。

解：首先，将小数点后各位二进制数的位权0.5，0.25，0.125，0.0625，……分别填入表格第一行的相应位置。

其次，计算十进制数0.8125中包含有哪些位权？并在相应位权的下面填写“1”。

0.8125 -0.5=0.3125，在位权0.5的下面填写二进制数“1”；

0.3125 -0.25=0.0625，在位权0.25的下面填写二进制数“1”；

0.0625 -0.0625=0，在位权0.0625的下面填写二进制数“1”；

二进制数其他空格里填写二进制数码“0”。

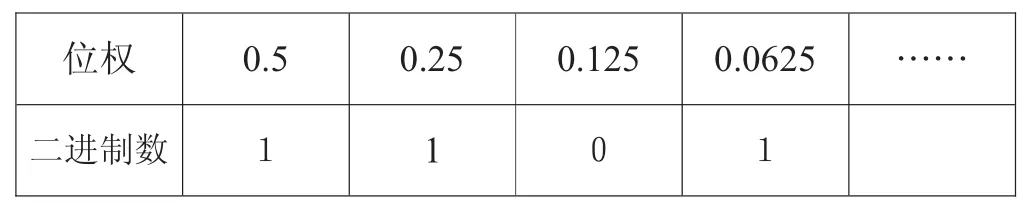
故 (0.8125)10＝（0.1101）2

通过以上的例子可知，将二进制数转换为十进制数时，只需将二进制数各位的位权先标注在二进制数各位上，然后将二进制数“1”位上的位权相加即可。若将十进制数转换为二进制数，先标注出二进制数各位上的位权，然后将十进制数依次比较二进制数各位的位权，如果十进制数中包含有二进制数各位上相应的位权，则在位权下面的二进制位上填写“1”，否则填写“0”。对于八进制、十六进制与十进制之间的转换，均可借助于二进制数相互转换，然后再转换为其他进制。故掌握了二进制数与十进制数之间的转换也就掌握了各种进制数之间的转换。

［1］ 王津.计算机应用基础［M］.西北大学出版社,2008.

［2］ 卢庆林.数字电子技术［M］.机械工业出版社,2008.

［3］ 董少明.单片机原理与应用技术［M］.北京理工大学出版社,2009.

［4］ 熊意强,周旭欣,杨小洪.数制转换的简易方法解析［J］.硅谷,2010,(01):53-54.

［5］ 张宏洲.数制转换的简便方法［J］.铜陵职业技术学院学报,2006,(03):90-91.

A Fast method Between Decimal and Binary Number Conversion

SUN Ji-long HUAN Mei-li
（Shaanxi polytechnic insititute,Xianyang 712000,Shangxi）

The conversion between decimal systemand binarysystemare difficulties in the course of"fundamentals ofComputer Application"etc.The conventional conversion methods are too cumbersome to accept for the beginners.This paper gives a brief method of conversion,named"8,4,2,1"labeled weight method,tohelp the students tounderstand and master efficiently.

numerical system;conversion;method

G623.4

［文章编号］ 1671-5004（2011） 03-0143-02

2011-5-5

孙继龙（1969-），男，陕西铜川人，陕西工业职业技术学院信息工程学院讲师，研究方向：软件工程。

桓美丽（1970-），女，陕西礼泉人，陕西工业职业技术学院信息工程学院辅导员。