基于理想形变理论的有限元逆算法在板料成形中的应用

朱光成，吴建军

（西北工业大学 机电学院，陕西 西安 710072）

基于理想形变理论的有限元逆算法在板料成形中的应用

朱光成，吴建军

（西北工业大学 机电学院，陕西 西安 710072）

基于理想形变理论，研究了金属板料成形的有限元逆算法，并开发了计算程序。采用线性三角形膜单元和厚向异性的刚塑性材料模型，计算了一个带凸缘的方盒形件，并与Dynaform的一步逆向法和增量法的计算结果进行了比较。实例分析结果表明，在工程允许精度范围内，本文方法能够有效分析零件的成形性能。由于该方法计算速度快，所以可用于零件的早期设计。

机械制造；板料成形；理想形变理论；有限元

1 引言

随着计算机技术的迅速发展和有限元理论的日趋成熟，有限元方法在坯料计算及板料成形中的应用越来越广泛。目前，常用的板料成形数值模拟方法主要有两种：基于增量理论（又称流动理论）的有限元增量法和基于全量理论（又称形变理论）的有限元逆算法。增量法可以全面考虑各种影响因素，是目前比较精确的方法。但在产品及工艺设计的早期阶段，通常只有产品形状而无模具信息，因而，使用增量法进行数值模拟比较困难。对设计人员来讲，最重要的是如何根据产品或已经完成工艺补充的冲压件几何形状来快速预测它的毛料展开形状和零件的厚度分布等信息，以此来预测零件的可成形性和工艺的可加工性。因此，K.Chung和O.Richmond将形变理论与极值功路径相结合，提出了理想形变的概念[1]。本文将其应用于板料成形过程，开发了有限元逆算法程序。采用线性三角形膜单元和厚向异性的刚塑性材料模型，计算了一个带凸缘的方盒形件，验证了本文方法的有效性。

2 理想形变理论[2]

理想形变的基本假设为：变形沿着最小塑性功路径进行，材料为刚塑性，满足R.Hill’79屈服准则。整个变形过程达到最小塑性功路径的条件有两个：塑性变形的主伸长对应于固定的主物质线；塑性变形的主自然应变比保持不变。

理想形变理论认为变形体在整体塑性功取得相对极值的条件下变形较为均匀。变形取得相对极值的条件为：在成形的最后一刻，变形体在边界上仅受法向力作用而处于平衡状态，且变形分布较为均匀，并以变形过程中消耗的整体塑性功最小作为应变优化的基础。文献[1]中已经对该假设做了证明。将变形过程看作一个匀速的过程，考虑到塑性变形体积不可压缩的假设，包括不均匀变形的塑性功可表示为：

式中：σ——Cauchy应力；

D——应变速率；

σ¯——等效应力；

ε¯——等效应变；

V0——初始体积。

当物质微元的变形路径确定之后，塑性功就只由位移确定，可看作是位移的函数W=W（U）。

3 理想形变理论的有限元表达及实现

3.1 变形分析[3][4]

在Lagrange描述法中，物质坐标系在初始构形中与整体坐标系重合。变形前，物质坐标系为直角坐标系，各坐标轴之间的夹角为直角，且基矢量为单位矢量。变形后，物质坐标系不再是直角坐标系。根据Kirchhoff假设，变形前的中面法线在变形后仍然垂直于中面。用P0和Pt分别表示物质点P在变形前后的空间位置，我们可以得到变形后物质坐标系在P点的基矢量t→1、t→2和t→3的表达式为：

由于已知毛坯形状为平板，所以单元的右Cauchy－Green变形张量[C]可表示为：

[C]的特征值为单元面内两个主伸长λ1、λ2的平方，则有：

根据塑性变形中体积不可压缩的假设，可得板料上各点的厚向伸长量λ3为：

右Cauchy－Green变形张量[C]也可由坐标旋转矩阵[M]与主伸长λi（i=1，2，3）表示为：

其中，坐标旋转矩阵[M]为：

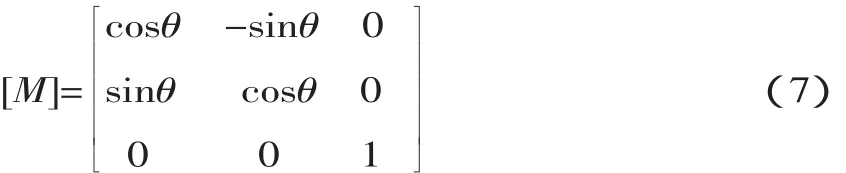
θ是λi与最终构形的局部坐标系x轴的夹角，求解（6）式得：

由右Cauchy－Green变形张量[C]容易得到对数主应变表达式为：

那么单元沿着厚度方向任意一点的大变形对数应变表达式为：

3.2 塑性功及其极值[5]

将理想形变应用于板料成形设计时，考虑到零件的最终构形和坯料的初始轮廓（一般是平面）是已知的，成形过程的边界条件未指定，最终构形上的物质点必须满足几何约束条件x3=x3（x1，x2）,再根据U= x-X（X，x分别是物质点在初始构形和最终构形上的节点坐标），取得整体塑性功极值的静力平衡方程：

采用Newton－Raphson迭代法，构造方程组，求{R（X）}=0，有：

定义切线刚度矩阵为：

求解方程组式（13），就可得到初始构形上节点坐标的调整量{d Xi}，调整后的节点坐标为：

式中：β——减速因子，取值一般为0～1，本文取为1。

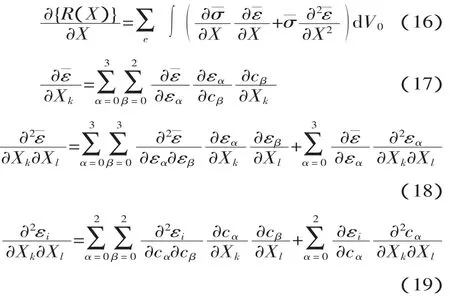
以上各式的具体表达形式可以非常容易的求得，故这里不再详细介绍。

3.3 程序流程图及毛料初始解的获取

在Visual C++6.0环境下开发有限元逆算法程序，程序的计算流程图如图1所示。

有限元逆算法需要一个毛料的初始猜测值。一个合理的毛料初始解将直接影响到求解的收敛性和准确性。本文采用几何映射法[6]获得该初始猜测值。

3.4 收敛准则及收敛性的提高[7][8]

采用Newton－Raphson迭代法必然存在两次迭代之间满足什么准则可以终止本次迭代的问题。根据有限元逆算法的实际计算情况，本文选择位移准则来进行收敛性判断，计算节点位移向量的范数：

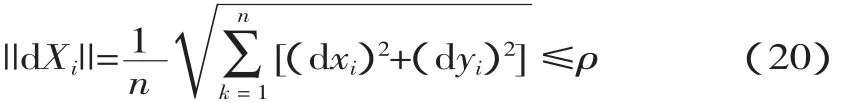
式中：n——节点总数；

ρ——给定的收敛判断因子，对位移收敛准则ρ一般取10－3。

当网格中出现畸变单元或单元大小突变比较严重时，可能使切线刚度矩阵呈现病态，程序算法无法收敛。为了提高逆算法的网格处理能力，添加阻尼矩阵来改善切线刚度矩阵的病态性。

由式（13）和式（14）可得：

图1 程序计算流程图

在切线刚度矩阵中加入阻尼矩阵δi[I]，[I]为单位矩阵，δi[I]为对角矩阵，则方程组的解为：

在本文程序算法中取：

式中：Kjj——第i迭代步中切线刚度矩阵第j行第j列的对角线元素值。

4 有限元逆算法应用实例

图2 划分有限元网格的产品最终构形

以尺寸为50mm×50mm×20mm、各处圆角半径均为6mm的带凸缘的方盒形件为例进行计算。图2是划分三角形单元后产品的最终构形。单元尺寸为2.5mm，盒形件划分为2384个单元和1237个节点。材料的应力应变曲线σ¯=520.4ε¯0.232MPa，厚向异性指数为r= 1.65，毛料的初始厚度为t=1.0mm。采用本文方法、Dynaform的一步逆向法和增量法的计算结果见3所示，三种方法计算的零件厚度的云图分布规律基本上是一致的，只存在个别区域的差异。本文方法与Dynaform一步逆向法相比：增厚最大误差为2.60%，减薄最大误差为 0.82%；本文方法与Dynaform增量法相比：增厚最大误差为12.84%，减薄最大误差为6.77%。采用Dynaform增量法用时1976s，而本文程序迭代6次就收敛，用时仅493s，本文方法明显比增量法快很多。本例计算是在Windows XP系统上完成的，CPU是AMD Processor 5050e/2.61GHz，内存为2GB。

在板料成形中，零件的厚度变化是一重要的因素，因为变薄严重会有破裂的可能，增厚严重会有起皱的可能，所以算例中主要对零件的厚度进行了分析和比较。

5 结论

根据理想形变理论结合板料成形的具体情况，给出了有限元逆算法的数学公式和有限元表达，开发了工程分析模块。同Dynaform的一步逆向法和增量法的计算结果进行对比，本文方法计算的零件厚度分布情况同实际情况更加吻合。由于本文方法在计算过程中简化了工艺参数对板料成形的影响，这样的结果在工程分析中是可以接受的。通过实例可以证明，有限元逆算法能够较好的满足设计的需要，是一种高效的数值模拟工具。虽然逆算法模拟精度相对于增量法低了一些，但随着算法的不断完善，其模拟精度还可以得到进一步的提高。

图3 零件的厚度分布

[1]K.Chung，O.Richmond.Idealforming-Ⅱ.Sheetforming withoptimum deformation[J].Int.J.Mech.Sci.，1992，34（8）:617-633.

[2] 兰 箭，董湘怀，李志刚.用有限元逆算法计算板料成形毛坯形状和应变分布[J].塑性工程学报，2001，8（2）:60-62.

[3] 吴建军，陈卫彬，李顺平.复杂形状拉深件快速展开与成形模拟[J].机械科学与技术，2004，23（3）:370-375.

[4] 陈卫彬.基于反向模拟法的拉深成形性分析技术研究[D].西安:西北工业大学出版社，2003.

[5] K.Chung，S.Y.Lee，F.Barlat.Finite elementsimulation ofsheetforming based on a planaranisotropic strain-rate potential[J].InternationalJournalofPlasticity，1996，12（1）:93-115.

[6] 吴建军，杨汉平.考虑外法向的钣金零件展开方法研究[J].中国机械工程，2006，17（15）:1546-1549.

[7] Y.Q.Guo，J.L.Batoz，H.Naceur.Recent developments on the analysis and optimum design of sheet metal forming parts using a simplified inverse approach[J].Computers and Structures，2000，78:133-148.

[8] 徐国艳，高 峰，杜发荣，张立玲.基于快速有限元分析的冲压件毛料展开[J].机械科学与技术，2006，25（4）:386-389.

Application of finite element inverse approach in sheet metal forming process based on ideal forming theory

ZHU Guangcheng，WU Jianjun
（Northwestern Polytechnical University, School of Mechatronics, Xi'an 710072，Shanxi China）

Based on ideal forming theory, the finite element inverse approach for sheet metal forming has been explored, and the computer program has been implemented. By use of the linear triangular membrane element and the thickness anisotropy rigid-plasticity material model，a flanged square box has been analyzed and its result has been compared with the results obtained from MSTEP and incremental approach of Dynaform software. The results show that the finite element inverse approach is an effective approach for sheet metal forming only if its error is allowable during the engineering calculation. Because of its rapid computing speed, this method can be used at the early design stage of sheet metal forming parts.

Sheet metal forming；Ideal forming theory；Finite element

TG386

A

1672－0121（2011）03－0049－03

国家863计划资助项目（2008AA04Z120）

2011－02－22

朱光成（1985－），男，硕士在读，主攻板料成形数值模拟技术