相位板装配倾斜对波前编码系统点扩散函数的影响

方 超

(中国科学院长春光学精密机械与物理研究所应用光学国家重点实验室，吉林长春130033)

1 引言

与传统成像系统不同，波前编码系统将光学技术和数字图像处理技术相结合，通过相位掩模板对被摄物体进行编码，不仅使光学系统的光学传递函数对离焦量不敏感，同时避免了部分空间频率的丢失。波前编码通过对所得中间图像进行解码来恢复图像，从而可在保证系统的光通量和成像分辨率的情况下，扩大系统焦深［1-3］。由于波前编码技术不仅能拓展系统的景深，而且能在一定程度上抑制球差、色差、匹兹法像面弯曲等像差，所以波前编码具有广阔的应用前景，并且已经取得了一定的进展［4-5］。

目前，对波前编码系统性质的研究多基于不存在安装误差的理想情况，而实际波前编码系统由于存在装配误差，编码所使用的相位掩模板不可避免地存在一定的倾斜误差。这一因素直接影响系统的广义光瞳函数，进而影响系统的点扩散函数和光学传递函数。因此，本文针对相位板安装倾斜的波前编码系统，通过坐标变换推导了倾斜系统的广义光瞳函数，分析了倾斜因子的相位板放大效果，并通过仿真模拟验证了这一理论。

2 理论分析

含有三次相位掩模板的波前编码系统如图1所示，其中虚线部分是放置相位掩模板的理想位置。在非相干光正入射的条件下，定义光轴沿z轴方向，则广义光瞳函数［6］的相位部分可表示为：

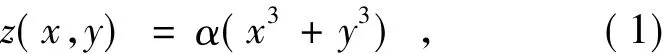
式中：x，y是光瞳上的点坐标，α是相位板参数。

在实际波前编码系统中，由于装调误差等因素的存在，相位板旋转一定角度β，就会导致相位板的广义光瞳函数发生变化，如图1实线所示。通过坐标变换的方法可以获得旋转后的广义光瞳函数。图1中坐标系xyz旋转β角后变为坐标系x'y'z'，则广义光瞳函数变为：

图1 含三次相位掩模板的波前编码系统Fig.1 Wavefront coding system with cubic phase mask

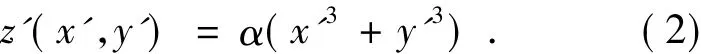
坐标系变换的关系式为：

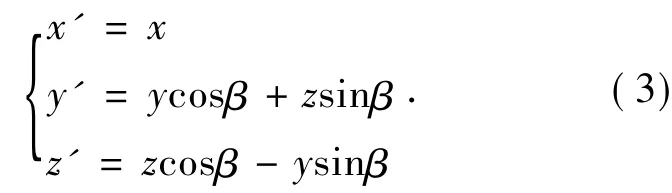
将式(3)代入式(2)，得出关于z的一个方程：

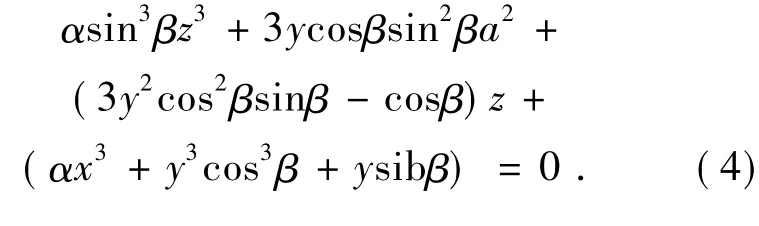
由于α很小，只有几个波长数量级，所以可以忽略含α的z高阶量，则z的近似解为：

由于 α 很小，所以 3αcos2βsinβy2较小，则：

忽略包含α的高阶项，展开得：

式中：tanβy表示主光线的位置发生了一个位移，考虑到它对波前编码系统成像质量影响很小，将其忽略。

令：

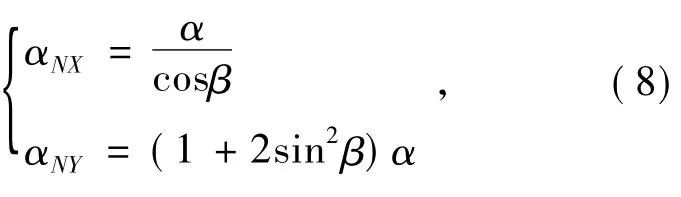
将式(8)代入式(7)得：

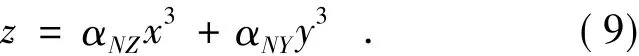
对比式(1)和式(9)可知，倾斜后的相位掩模板仍然是一块三次相位掩模板，只是相位板的参数发生了变化，且子午方向和弧矢方向的参数不同。具体变化情况如图2所示，子午方向和弧矢方向的相位板系数在倾斜前后的比值均大于1，说明倾斜后三次相位板的系数均被放大;相位板系数的放大效果仅与旋转角度的绝对值有关而与符号正负无关;相位板系数放大效果随倾斜角度的增大而增大，并且子午方向的放大效果要强于弧矢方向。

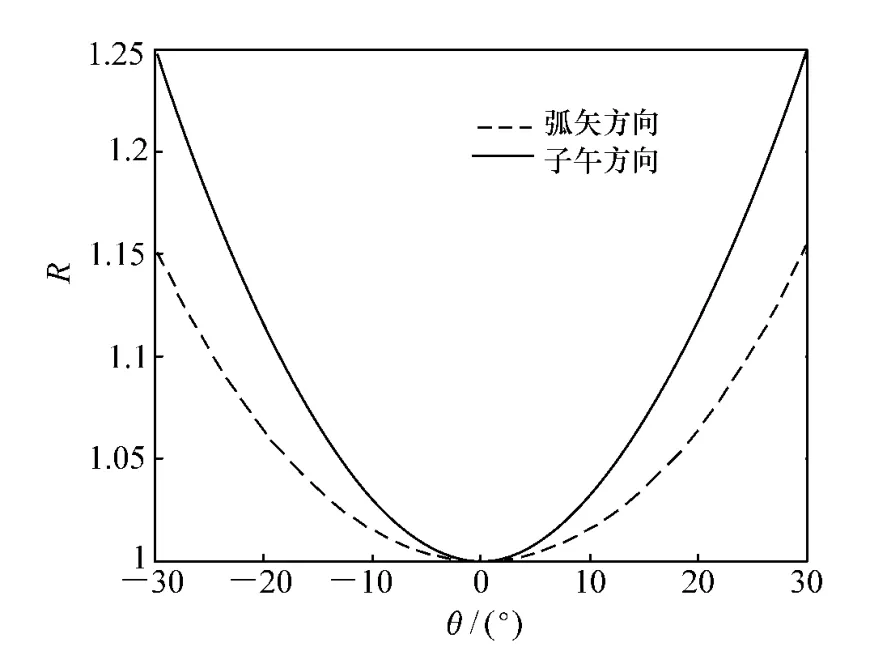
图2 相位板系数比Fig.2 Ratio of phase mask coefficients

考虑到系统离焦因素的影响，整个系统的广义光瞳函数可表示为：

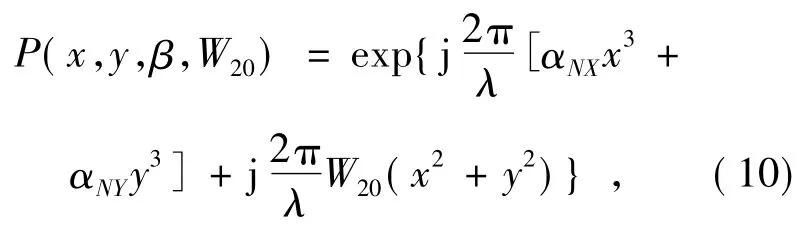
式中：λ为入射光的波长，W20为离焦量参数。

一个点物在像平面上产生的输出函数称为点扩散函数(PSF)。对广义光瞳函数进行傅里叶变换，再对其取模的平方就可以得到系统的PSF［7］，PSF傅里叶变换后的模即为系统的光学传递函数(MTF)，分别如式(11)和(12)所示。

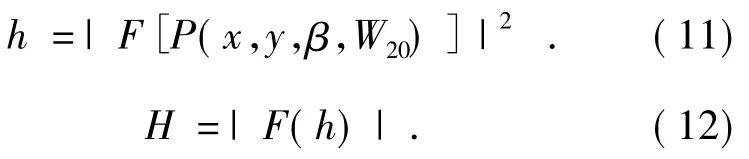
根据式(1)，可得：

式(13)说明x，y是轮换的，所以如果倾斜发生在弧矢平面，会有类似的结论，只不过弧矢方向的放大效果大于子午方向。

3 仿真模拟

仿真光学系统的光瞳直径为2 mm，波长为587.561 8 nm，成像透镜的焦距为15 mm，相位掩模板的参数为10λ，子午面绕x轴旋转倾斜，采用控制变量法分析点扩散函数性质。

当倾斜角β为30°时，模拟系统的点扩散函数如图3所示，其中(a)对应离焦量W20为0，(b)为2.5λ，(c)为5λ。

图3 β=30°时不同离焦量的点扩散函数图Fig.3 PSF with different defocuses when β =30°，

由图3可知，当相位掩模板倾斜时，不同离焦量的点扩散函数不变，这个特性有利于后续的图像恢复。

当离焦量为5λ时，模拟系统的点扩散函数如图4所示，其中(a)对应倾斜角β为0°，(b)为15°，(c)为30°，(d)为 -30°。

由图4(a)～4(c)可知，系统的点扩散函数随倾斜角的增大而被放大，并且在子午方向的扩展效果要强于弧矢方向，点扩散函数的形状由等边三角形退化为不等边三角形，点扩散函数的形状发生较大变化，因此，依靠点扩散函数的图像恢复算法在不考虑根据倾斜角修正点扩散函数时，图片的恢复质量将受到严重影响。比较图4(c)和图4(d)，点扩散函数未发生变化，说明倾斜角的正负对点扩散函数没有影响，只与绝对值有关，因此与广义光瞳函数的结论相对应。

图4 不同倾斜角的点扩散函数图Fig.4 PSF with different angles when W20=5λ

为了验证上述结论，利用光学软件，采用相同的参数对上述系统进行了仿真，其点扩散函数分别如图5和图6所示。

图5 光学软件中β=30°时不同离焦量的点扩散函数图Fig.5 PSF with different defocuses in optical software when β =30°

图6 光学软件中W20=5λ时不同倾斜角的点扩散函数图Fig.6 PSF with different angles in optical software when W20=5λ

对比图3、图5以及图4、图6可见，从光学软件中获得的点扩散函数的变化规律与前面的分析基本一致，说明用这种近似方法研究相位板倾斜对波前编码系统点扩散函数的影响是可行的。

利用光学软件获得了不同倾斜角不同倾斜方向时系统的MTF值。图7表示对应0°和30°这两个角度的MTF，当倾斜角为0°时，子午和弧矢方向的MTF趋向重合，随着倾斜角的增大，系统的MTF曲线逐渐减小，并且子午方向减小的程度大于弧矢方向，这样会导致子MTF曲线与弧矢MTF曲线分离，降低后期图像恢复的质量。

图7 不同倾斜角和不同倾斜方向时的MTF曲线Fig.7 MTF curves of different angels and directions

4 结论

本文分析了波前编码系统中的关键部件相位掩模板在装调过程中发生倾斜对系统的影响。通过坐标变换，获得相位掩模板在倾斜后的近似表达式，进而推导出这种情况下的点扩散函数。结果表明：相位板倾斜的波前编码系统的点扩散函数会受倾斜影响而被放大，在子午倾斜的情况下，子午方向的放大效果要大于弧矢方向，这将在很大程度上影响基于点扩散函数的恢复算法对图像恢复后期的效果，且MTF曲线会相应地随之降低，子午方向MTF曲线减小程度也会大于弧矢方向。该方法不仅可以应用于三次相位板系统，也可以用于其它形式的波前编码系统性质的分析，为分析装配误差对系统的影响提供了依据。

［1］ DOWSKI E R，KENNETH J R，KUBALA S.Modeling of wavefront coded imaging systems［J］.SPIE，2002，4736：116-126.

［2］ NARAYAMY R，BARON A E，CHUMACHENKO V，et al..Application of wavefront coded imaging［J］.SPIE，2004，5299：1-12.

［3］ DOWSKI E R，JOHNSON G E.Wavefront coding：a modern method of achieving high performance and/or low cast imaging systems［J］.SPIE，1999，3779：137-145.

［4］ 蔡怀宇，方超，范立强，等.混凝土结构裂缝宽度波前编码测量系统的设计［J］.光学 精密工程，2009，17(11)：2750-2756.CAI H Y，FANG CH，FAN L Q，et al..Image restoration of wavefront coding system with a cubic phase mask［J］.Opt．Precision Eng．，2009，17(11)：2750-2756.(in Chinese)

［5］ 蔡怀宇，方超，范立强，等.基于立方型相位板调制的波前编码图像恢复［J］.光电子激光，2010，21(6)：930-934.CAI H Y，FANG CH，FAN L Q，et al..Design of wavefront coding system for measuring crack width in concrete structure［J］.J Optoelectronics Laser，2010，21(6)：930-934.(in Chinese)

［6］ DOWSKI E R，CATHEY W T.Extended depth of field through wavefront coding［J］.Appl．Opt．，1995，34(11)：1859-1866.

［7］ 苏显渝，李继陶.信息光学［M］.北京：科学出版社，1998：133-170.SU X Y，LI J T.Information Optics［M］.Beijing：Science Press，1998：133-170.(in Chinese)