线性加速度计在压电陀螺卡尔曼滤波技术中的应用

林旻序，汪永阳，戴 明，乔彦峰

(1.中国科学院长春光学精密机械与物理研究所，吉林长春130033;2.中国科学院 研究生院，北京100039)

1 引言

光电稳定平台作为侦察、测量、校射和打击效果评估的重要技术支撑，其视轴稳定精度决定了整个系统性能的好坏。而提高视轴稳定精度，必须对惯性速率反馈元件陀螺的噪声加以约束。目前小型光电稳定平台常采用压电陀螺作为惯性传感器，由于压电陀螺随机游走噪声较大，通常采用二阶或高阶巴特沃思低通滤波对其进行滤波，虽然这种方法能够对高频噪声起到很好的抑制作用，但同时会产生陀螺低频信号的相位延迟，从而影响陀螺信号带宽［1］。

本文在设定压电陀螺速率状态变量的基础上，运用卡尔曼滤波理论建立状态递推、状态估计以及滤波增益等方程，从而完成对压电陀螺信号的滤波。由于在状态递推的过程中采用了压电陀螺的角加速度信号，从而引入系统噪声，因此滤波后陀螺信号的噪声水平和带宽在很大程度上依赖于加速度信号。

目前惯性角加速率的测量方法较少，一般采用CJ4、CJ6两款角加速度陀螺，因为其采用压电陀螺角速率差分原理，从而带宽上限只能达到50 Hz，无法保证卡尔曼滤波后陀螺的相位延迟。本文通过在光电平台内框架跨轴安装3个线性加速度计间接测量平台的惯性角加速度，通过对线性加速度计的选型，很好地控制了卡尔曼滤波后陀螺信号的噪声和带宽。

2 压电陀螺噪声特性

为了分析压电陀螺测量信号的噪声特性，取平台静止不动时的测量信号(零位测量信号)序列数据为研究对象，图1为压电陀螺零位测量信号曲线。陀螺噪声随机过程是各态历经的随机过程，因此对噪声特性的分析，必须对其进行傅里叶变换得到其功率谱，随后根据噪声频率域的分布情况对其进行滤波。

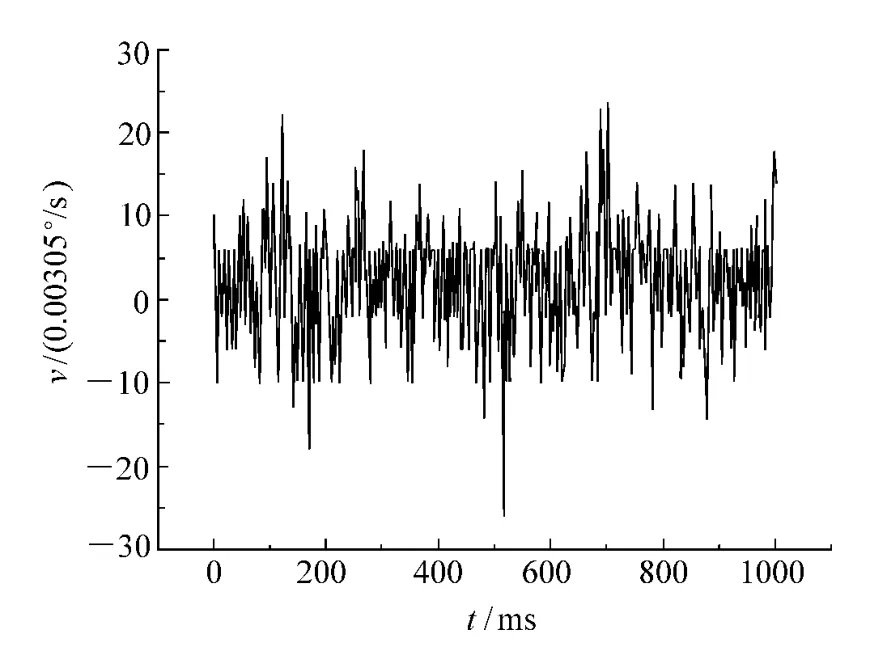
图1 压电陀螺零位测量信号曲线Fig.1 Zero-position test signal curve of piezoelectric gyro

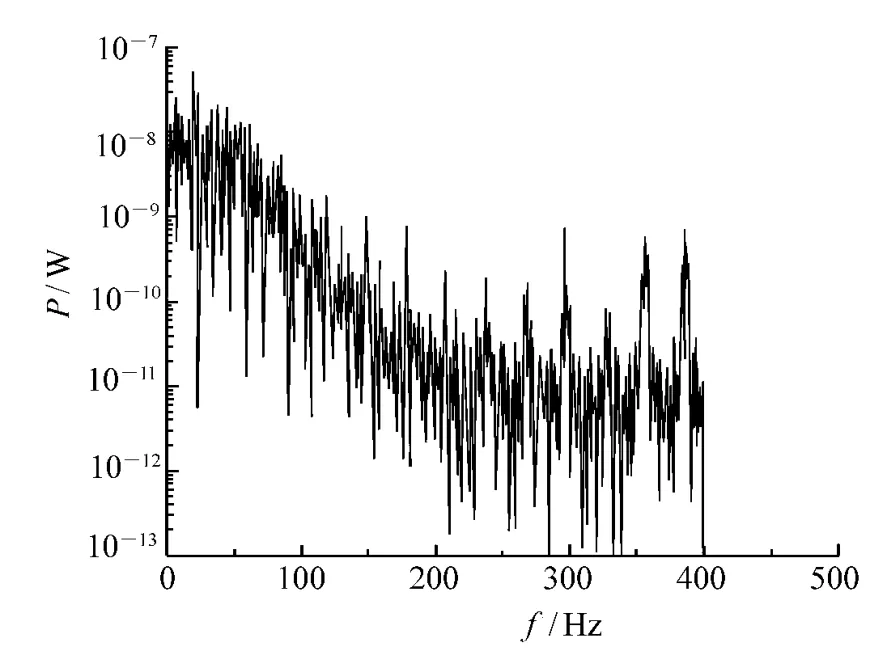
图2 压电陀螺噪声功率谱Fig.2 Noise power spectrum of piezoelectric gyro

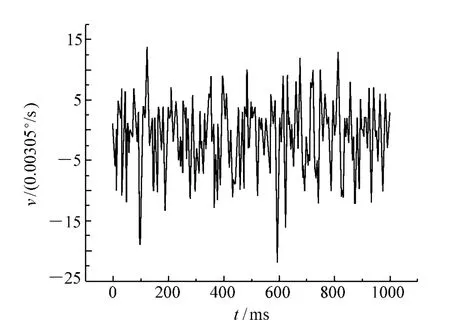
图3 经50 Hz巴特沃思低通滤波后的压电陀螺零位信号曲线Fig.3 Zero-position test signal curve of piezoelecric gyro filted with 50 Hz Butterworth

压电陀螺噪声功率谱如图2所示，可以看出噪声功率谱密度值在低频段较为突出，若采用巴特沃思低通滤波或均值滤波，只能消除噪声的高频段信息，对压电陀螺噪声不能起到明显的抑制作用，而采用二阶或高阶低通滤波器，极易引起压电陀螺信号的相位延迟，从而影响整个伺服系统的控制带宽，图3为采用50 Hz二阶巴特沃思低通滤波器滤波后的压电陀螺零位测量信号［2-3］。

3 卡尔曼滤波器的应用

以离散系统为例，设tk时刻的被估计状态Xk受系统驱动噪声序列Wk-1驱动，驱动机理由下述状态方程描述［4］：

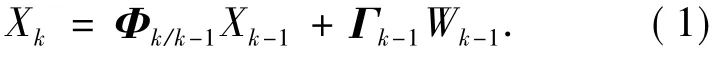
对Xk的量测满足线性关系，量测方程为：

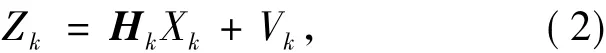
式中：Φk/k-1为tk-1时刻至tk时刻的一步转移矩阵，Γk-1为系统噪声驱动矩阵，Hk为量测矩阵，Vk为量测噪声序列，Wk为系统激励噪声序列。同时，Wk和Vk满足［5］：

式中：Qk为系统噪声序列的方差阵，假设为非负定矩阵;Rk为系统测量序列的方差阵，假设为正定矩阵。

状态一步预测［6］：

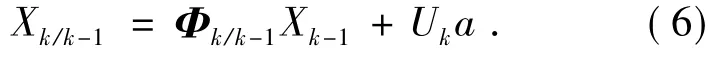
状态估计：

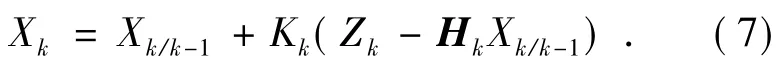
滤波增益：

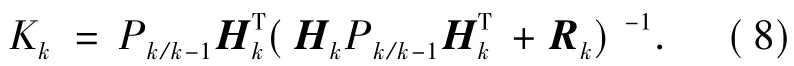
一步预测均方误差：

估计均方误差：

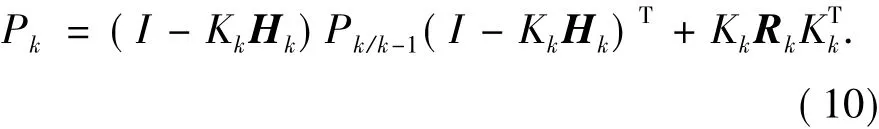
卡尔曼滤波过程如图4所示。

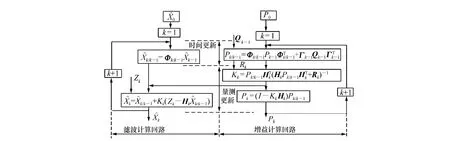
图4 卡尔曼滤波的两个计算回路和两个更新回路Fig.4 Two calculating and updating loops in Kalman filtering method

图中状态变量Xk为k时刻所估计的压电陀螺速度;Φ=1;Uk为采样周期T;Zk为压电陀螺仪在k时刻速度的测量量;Hk=1;Rk为陀螺自身的噪声方差;Qk为加速度计自身的噪声方差。

采用卡尔曼滤波器滤除压电陀螺噪声，必须先获得平台的角加速度a以及角加速度测量噪声方差Wk。

4 线性加速度计测量角加速度原理

图5为采用一对线加速度计测量平台角加速度的原理示意图，平台的转轴垂直于纸面，一对线加速度计A1和A2同向平行地安装于平台上，敏感轴间距为L。

设线加速度计测得的线加速度为a1(t)和a2(t)，则平台的惯性角加速度a可由下式表示：

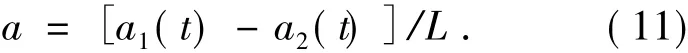
从图5可以看出，不论平台的转轴在两个加速度计的连线上，还是在两个加速度计连线的延长线上，或是根本不在两个加速度计的延长线上，式(11)均成立。

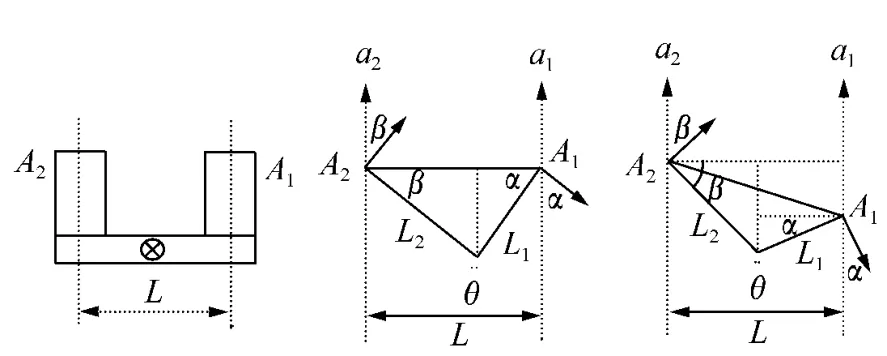
图5 线加速度计测量角加速度示意图Fig.5 Schematic of angle acceleration measured with linear accelerometer

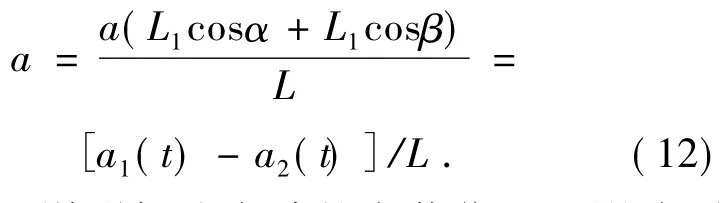
式(12)说明加速度计的安装位置不影响测量结果，所以实际系统中可以根据安装空间的位置任意安装加速度计。根据这一原理，测量互相垂直的两个轴向的角加速度，只需要3个线加速度计，如图6所示。

图6 3个线加速度计测量两轴角加速度示意图Fig.6 Schematic of two-axis angle acceleration measured with three linear accelerometers

3个线加速度计呈三角形位置，设加速度计A1，A2，A3的输出分别为a1(t)，a2(t)和a3(t)，则两个方向的角加速度为［4］：

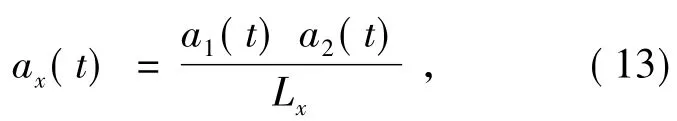
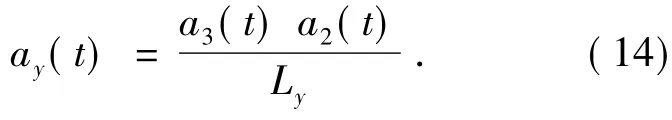
利用线性加速度计得到平台的角加速度后，可以从角加速序列中统计得到Qk。

图7(a)为压电陀螺的原始噪声曲线，图7(b)为卡尔曼滤波后的压电陀螺噪声曲线，图中纵坐标为0.003 05(°)/s。实际计算时。压电陀螺噪声方差Rk=35，加速度计噪声方差Qk=0.3;T=0.001 25 s。

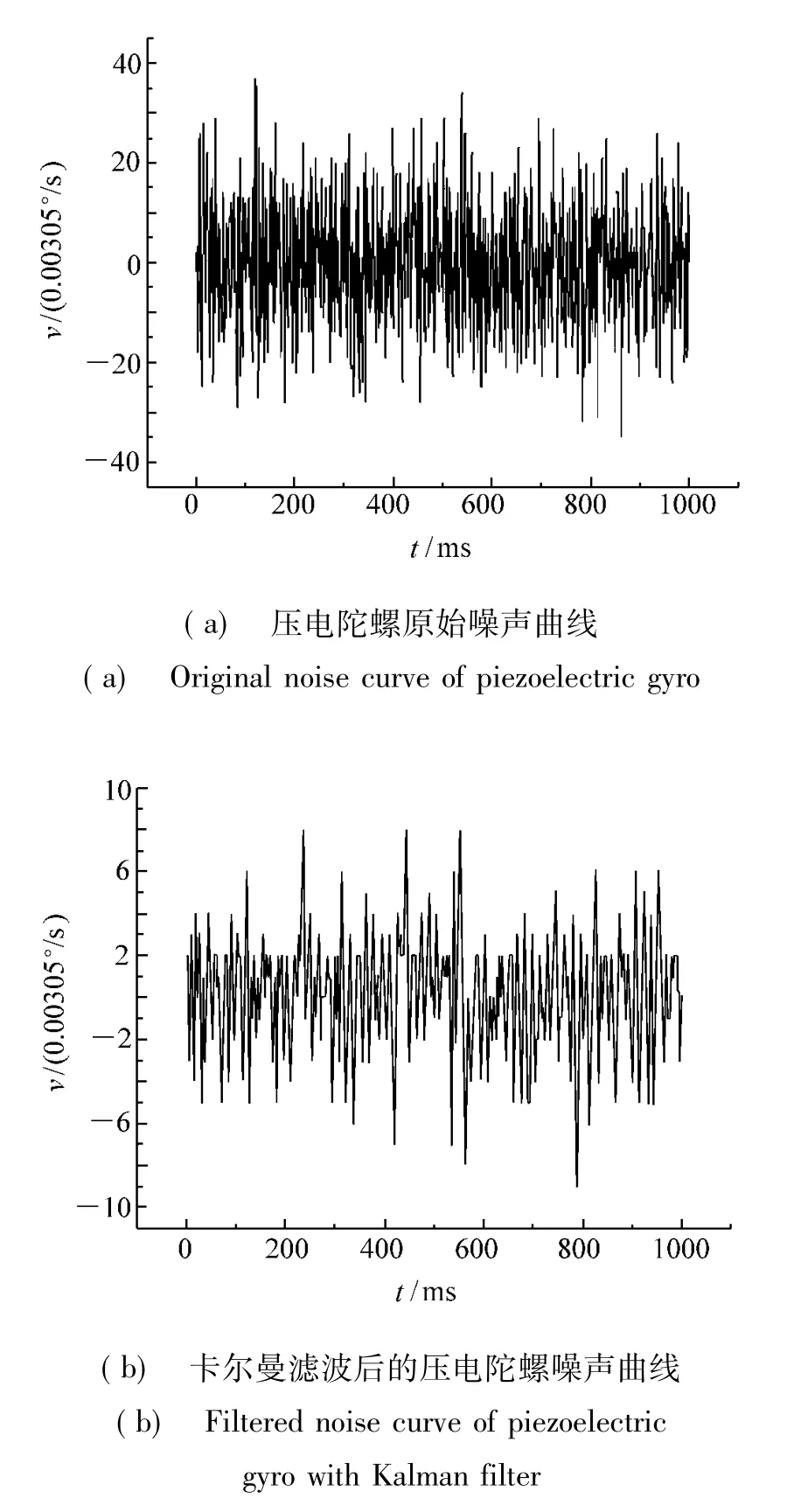
图7 压电陀螺噪声曲线Fig.7 Noise curves of piezoelectric gyro

可以看出若加速度计的噪声方差Qk=0.3，那么其噪声的标准差 σk= ■0.3≈055，则由于加速度计所引入的噪声水平最大值为3×σk×T≈

(°)/s，从而 0.002(°)/s作为卡尔曼滤波过程中的系统噪声，最大程度地影响着卡尔曼滤波的效果，实验中采用CF-1型线加速度计，标称带宽为100 Hz，噪声均方根值为300 μg(考虑 AD采样的影响)。

通过对图7(a)和图7(b)分别求功率谱变换曲线，可以得到图7(a)压电陀螺随机游走噪声水平为0.005(°)·s-1/ ■Hz，图7(b)卡尔曼滤波后压电陀螺随机游走噪声水平为0.001 25(°)·s-1/ ■Hz，图3中经50 Hz二阶巴特沃思低通滤波器滤波后的随机游走噪声水平为0.002(°)·s-1/■Hz。

虽然采用线性加速度计进行卡尔曼滤波后压电陀螺的噪声水平约为采用巴特沃思滤波器的2/3，但采用基于线性加速度计的卡尔曼滤波器在相位延时上却明显优于巴特沃思低通滤波器。图8和图9分别给出了开环2 Hz和15 Hz的情况下，采用卡尔曼滤波和巴特沃思低通滤波器的压电陀螺反馈曲线，其中实线为采用卡尔曼滤波器后的反馈曲线，虚线为采用50 Hz二阶巴特沃思滤波器滤波后的反馈曲线。

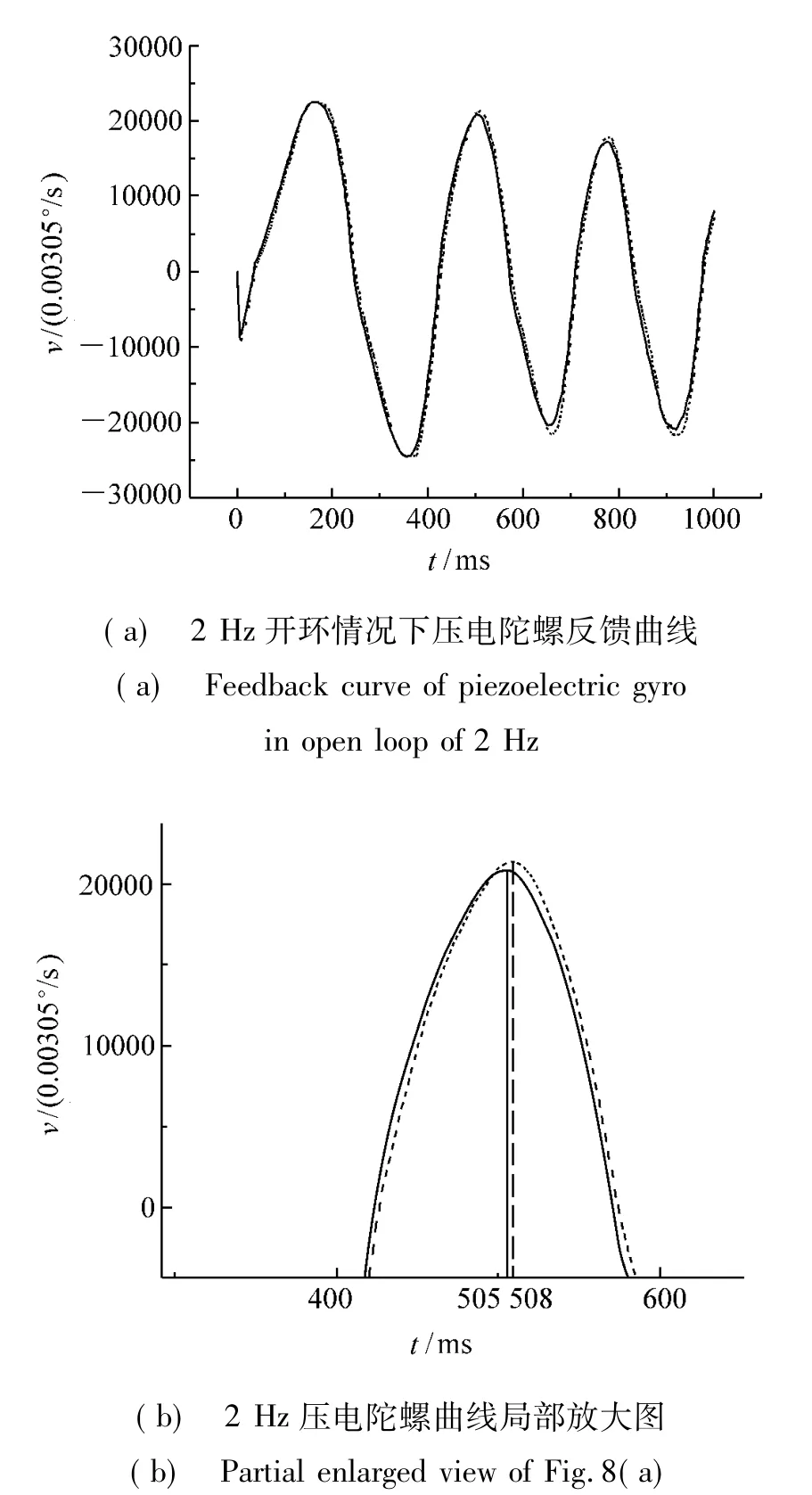
图8 2 Hz压电陀螺开环曲线图Fig.8 Curves of piezoelectric gyro in open loop of 2 Hz

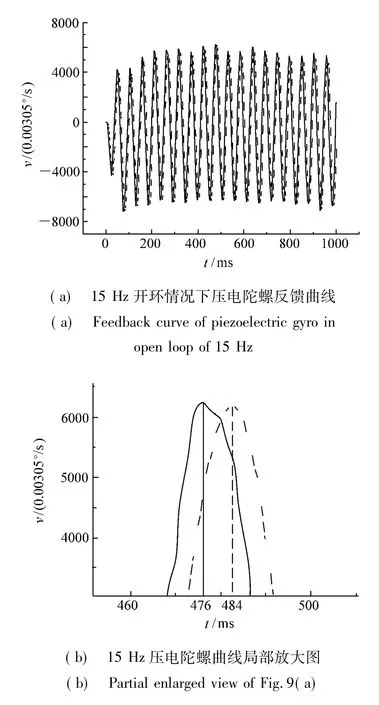
图9 15 Hz压电陀螺开环曲线图Fig.9 Curves of piezoelectric gyro in open loop of 15 Hz

通过图8(b)两条曲线峰值的延时可以看出，2 Hz时卡尔曼滤波器的相位超前二阶巴特沃思滤波器3 ms，等效于(3/500)×360=2.16°。通过图9(b)两条曲线峰值的延时可以看出，15 Hz时卡尔曼滤波器的相位超前二阶巴特沃思滤波器8 ms，等效于(8/66.67) ×360=43°。因此随着频率的升高，巴特沃思滤波所带来的延迟也会逐渐加大，而卡尔曼滤波则保持很好的相位特性。

图10给出了原始噪声、采用CF-1加速度计滤波后的噪声以及采用更高精度线性加速度计滤波后的噪声对稳定精度的影响。

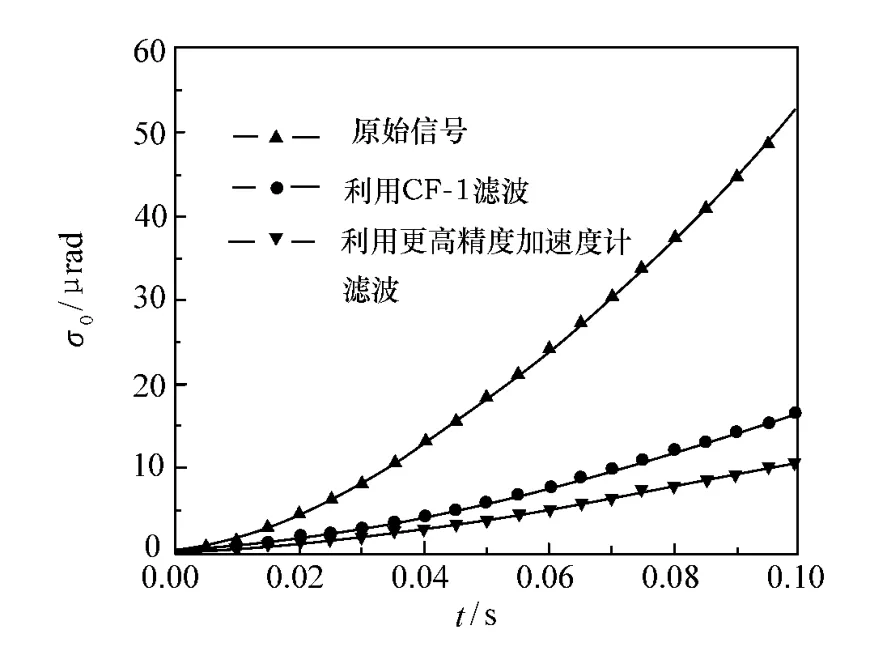
图10 压电陀螺噪声对稳定精度的影响Fig.10 Influence of piezoelectric gyro noise on stabilization accuracy

5 结论

针对目前小型光电稳定平台上广泛应用的压电陀螺随机游走噪声大的问题，提出采用基于线性加速度计的卡尔曼滤波技术对其进行信号滤波。结果表明：采用卡尔曼滤波能够在保持压电陀螺带宽(最小相位延迟)的前提下，依靠高精度线性加速度计，充分消除原始陀螺信号中的白噪声。

［1］ MYUNG H，LEE H K，CHOI K，et al..Constrained Kalman filter for mobile robot localization with gyroscope［C］.Intelligent Robots and Systems，2006 IEEE/RSJ International Conference on，Beijing，China，9-15 Oct.，2006：442-447.

［2］ 毕永利.多框架光电平台控制系统研究［D］.北京：中国科学院研究生院，2003.BI Y L.Study on control system of multi-frame photoelectric platform［D］.Beijing：Graduate University of Chinese Academy of Sciences，2003.(in Chinese)

［3］ ALMAGBILE A，WANG J L，DING W D.Evaluating the performances of adaptive Kalman filter methods in GPS/INS integration［J］.J．Global Positioning Systems，2010(9)：33-40.

［4］ 王江安，庄奕琪，周淇军，等.利用改进卡尔曼滤波算法抑制GPS接收相位噪声［J］.数据采集与处理，2010(5)：611-614.WANG J A，ZHUANG Y Q，ZHOU Q J，et al..The application of Kalman filter in the suppression of GPS receiving phase noise［J］.Data Acquisition and Processing，2010(5)：611-614.(in Chinese)

［5］ 潘博文.卡尔曼滤波算法在相对导航中的应用［J］.现代导航，2010(4)：15-18.PAN B W.The application of Kalman filter in the relative navigation［J］.Modern Navigation，2010(4)：15-18.(in Chinese)

［6］ 赵延.机动目标自适应卡尔曼滤波算法研究［D］.西安：电子科技大学，2004.ZHAO Y.Study on adaptive Kalman filter for the maneuvering target［D］.Xi'an：University of Electronic Science and Technology of China，2004.(in Chinese)