冷原子介质中基于相干诱导高反射带和高透射带的全光路由控制

国秀珍，侯丽新，尹昭泰，吴金辉

(1.长春理工大学光电信息学院，吉林长春130012;2.吉林大学物理学院，吉林长春130012)

1 引言

近20年来，量子信息技术的蓬勃发展不但使人们深刻理解了物理世界的量子本性，还极大地提升了人们对微观量子系统的操控能力。当前，以量子力学原理为基础的量子网络通讯正在吸引着越来越多科学家们的研究热情，这有望推动经典计算和保密通讯等领域的革命性进展［1，2］。光子由于具有传播速度快、高度并行和对环境不敏感等特点而成为量子信息的理想载体。但是，要把光子限制在一个亚毫米的极小空间内并对其进行目的性较强的有效操控却并不容易。于是，研究多个单频相干激光与超冷原子系综等不同类型物质的共振相互作用显得极为重要。事实上，人们利用单频相干激光与多能级原子共振相互作用产生的量子干涉效应，已在线性吸收得到理想抑制的前提下得到了显著增强的非线性克尔效应，进而实现了对弱光信号的有效控制，例如可逆光学存储和量子逻辑运算［3～6］等等。然而，要实现规模化的量子网络通讯，还需要有高效的全光开关和全光路由等量子器件对信息进行选择性传输，使纠缠的信息载体经由网络通道分布于各个网络结点之中。迄今为止，已有的几个可用于量子信息处理的全光路由控制方案主要是利用双光子的相干交换［7］、光信号的绝热频率变换［8］、基于慢光的共振四波混频［9］和动态可控光子带隙结构［10］实现的。

光子晶体［11］是一种天然或人造的折射率周期分布的非均匀材料。由于空间周期结构会对电磁波产生Bragg散射，光信号在其中的传播过程可用类似电子能带结构的光子带隙结构［12］来描述。通常，光子晶体在制备完成后是不可调整的，其带隙位置和宽度等参数是固定不变的。然而，近来人们发现，利用相干激光与合适介质的共振相互作用可产生动态可控的光子带隙结构［13～15］，从而使光子晶体有望在量子信息处理领域得到更好的应用。本文重点介绍一种以相干诱导光子带隙结构为工作基础的新型全光路由控制方案。

2 全光路由控制的物理实现

图1 与探测激光ωp、耦合激光ωc和光栅激光ωg相互作用的一个四能级Tripod型超冷铷原子能级图Fig.1 Level diagram of four-level tripod-type cold87Rb atom interacting with probe laser ωp，coupling laser ωc ，and grating laser ωg

如图1所示，四能级Tripod型原子与较弱探测激光ωp、行波耦合激光ωc和驻波光栅激光ωg相互作用，频率失谐为 Δp=ωp-ω30，Δc=ωcω31，Δg=ωg-ω32。下面，总是假定能级|0〉、|1〉、|2〉和|3〉分别对应着超冷87Rb原子D1线上的|5S1/2，F=2，mF=1〉、|5S1/2，F=1，mF=-1〉、|5S1/2，F=1，mF=1〉和|5P1/2，F=2，mF=0〉这 4个超精细磁子能级。在这种情况下，所需要的波长近似为795 nm的3个相干激光ωp，ωc和ωg可由两个半导体激光器和一个声光调制器提供。假定光栅激光是一个完美驻波，即沿z轴传播的前向分量和后向分量幅度相等，则其拉比频率的平方可表示为|Ωg|2=4Ω2g0cos(kgz)。显然，驻波强度变化的周期为波长的一半(a=λg/2)。如果小幅度改变前向分量和后向分量的传播方向，使二者有一个很小的夹角θ，驻波强度周期将变为a=λg/［2cos(θ/2)］。经典电磁学理论表明，较弱探测激光可能会受到驻波Bragg光栅的相干散射而经历光子带隙结构，这可通过计算传输矩阵［13］得以证实。

根据传输矩阵理论，z处和z+a处的探测光可通过一个幺正矩阵M联系起来，即：

再根据Bloch定理，进一步获得：

这里k=k'+ik″是Bloch波矢。式(2)有非零解的条件是：

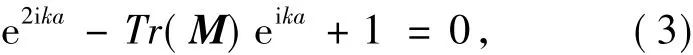
其中，满足|Tr((M)|＜2的区域对应实数 k，即Bloch波的传播解;满足|Tr((M)|＞2的区域对应复数k，即Bloch波的衰减解。如果在探测光的某一频带内|Tr((M)|＞2成立，则该频带可称为探测光的光子带隙。入射探测光波的这种衰减是由Bragg散射引起的，因此光子带隙的质量好坏主要体现为对应的反射率是否足够大。对于有N个周期的长度L=Na的一个原子系综，其反射光谱和透射光谱要由涵盖了所有N个周期的传输矩阵MN来确定，即：

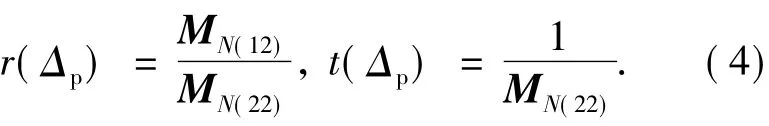
而MN可通过如下方式由M得到：

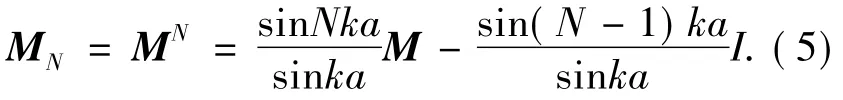
可见，为了验证对应着均匀高反射率的光子带隙是否存在，首先需要计算对应单个周期结构的传输矩阵M，这就需要知道介质的折射率n=。对图1所示的Tripod型原子系统，其电极化率可通过求解稳态密度矩阵方程得到：

式中N0代表原子密度，γi代表密度矩阵元ρ0i的退相干速率。

如图2所示，选择合适的参数后，通过上述理论可计算得到一个完美的光子带隙。虚线表明：当行波耦合激光强度为零，即四能级系统退化成三能级系统时，不能形成完美的光子带隙结构，这是因为驻波节点处的光强为零，以至于介质具有很强的吸收，从而破坏了光子带隙结构。为了克服节点处的吸收，一个可行的方法是令行波耦合激光强度不为零(使三能级系统恢复为四能级系统)，即利用行波耦合激光建立的量子干涉效应抑制驻波节点处的较强吸收，进而完善和改进光子带隙结构(参见实线)。

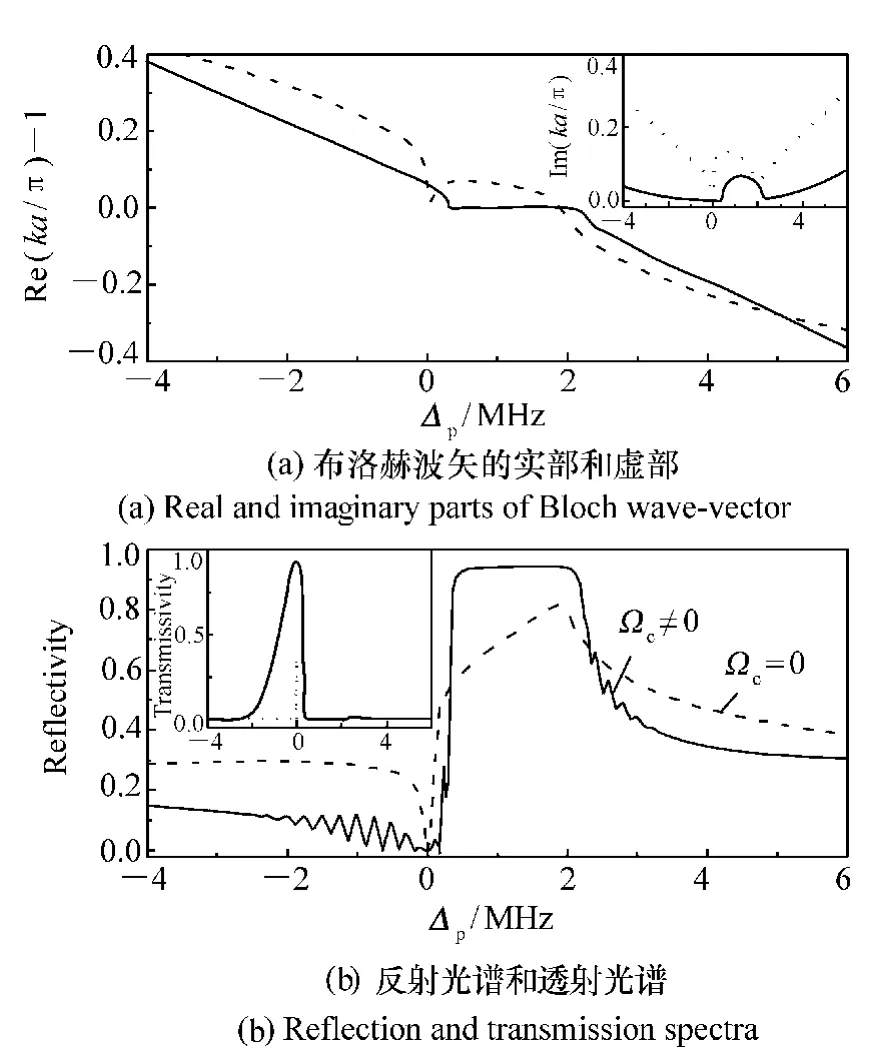
图2 探测跃迁上的相干诱导光子带隙结构，虚线对应Ωc=0;实线对应Ωc=9 MHzFig.2 Photonic band-gap structure on probe transition with Ωc=0 for dashed curve while Ωc=9 MHz for solid curve

如果进一步令行波耦合激光和驻波光栅激光具有不相等的频率失谐，可使二者的有效作用光谱区间在一定程度上有所分离，从而在探测跃迁上同时观察到宽度大致相等的一个高反射带和一个高透射带。经过简单的计算和分析容易知道：高反射带和高透射带的位置分别由驻波光栅激光和行波耦合激光的频率失谐决定，而其宽度则主要由行波耦合激光和驻波光栅激光的强度(正比于拉比频率的平方)决定。这样就可以方便地控制这两个特殊频带的位置，例如实现这两个频带的平移和交换，如图3所示。

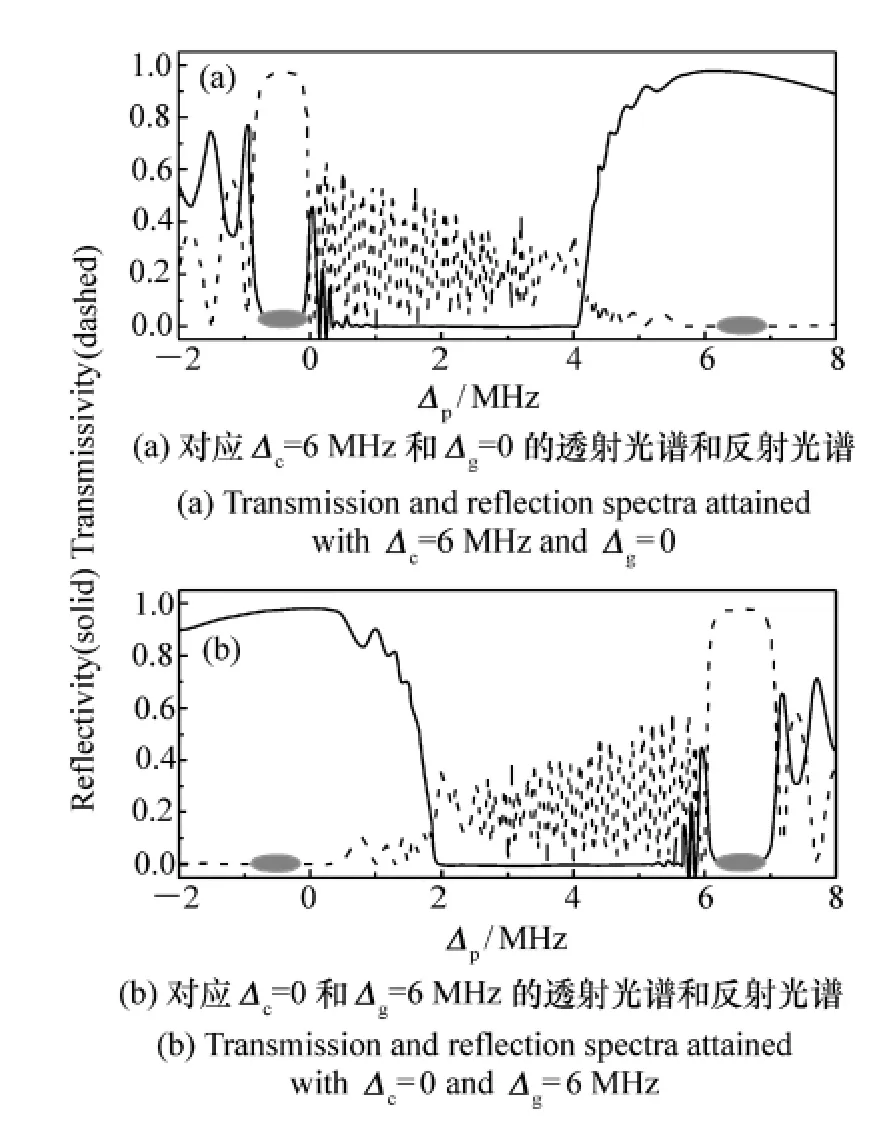
图3 对应两组不同参数的透射光谱(实线)和反射光谱(虚线)。4个实心椭圆用来指示两个高反射带和两个高透射带的位置Fig.3 Transmission spectra(solid)and reflection spectra(dashed)for two sets of different parameters.Four filled circles denote two high reflection bands and two high transmission bands，respectively

利用位置和宽度动态可控的高反射带和高透射带，可实现一个全光路由控制方案。假定A，B和C是一个通信网络中的3个结点并且结点B中存放有大量Tripod型超冷铷原子。当两个不同频率的光信号1和2进入结点B时，可通过控制行波耦合激光和驻波光栅激光使一个信号在反射后进入通向节点A的r-信道，使另一个信号在透射后进入通向节点C的t-信道。下面在信号1和2均为微弱高斯脉冲的情况下，借助傅里叶变换方法具体讨论如何实现基于相干诱导高反射带和高透射带的全光路由控制功能。

如果结点B前的探测信号1和2在时间域和频率域分别具有如下形式：

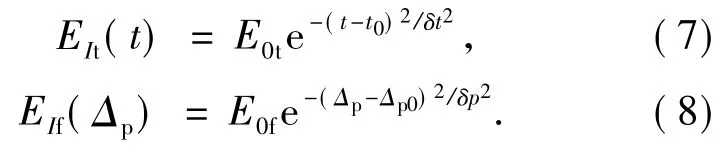
则在经过与节点B中Tripod型超冷铷原子的作用后，反射脉冲和透射脉冲可表示为：

图4 两个弱光信号的全光路由控制过程Fig.4 All-optical routing dynamics of two weak light signals

基于上述公式，即可以通过数值计算方便地分析信号1和信号2在节点B中的动力学传播过程。首先，为了对信号1和信号2进行同步操控，令它们在时间上和空间上完全重叠。根据图3中高反射带和高透射带的位置和宽度，将信号1和2的中心频率分别选择为 Δp01=-0.5 MHz和Δp02=6.5 MHz，并令脉冲宽度同为δp1=δp2=0.25 MHz，以便使它们的绝大多数载频落入高反射带和高透射带。如果结点B中超冷铷原子的反射光谱和透射光谱如图3(a)所示，则信号1将会被反射进入通向结点A的r-信道，信号2将会在透射后进入通向结点C的t-信道。如果结点B中超冷铷原子的反射光谱和透射光谱如图3(b)所示，则对应路由控制的传输过程会完全相反，即信号1被透射进入t-信道，而信号2被反射进入r-信道。这两个路由控制过程(参见图4(a)和图4(b))是通过动态交换高反射带和高透射带的位置而得以实现的。由图4还可知道，反射信号和透射信号相对入射信号均有一定的时间延迟，但是所经历的损耗(约5.3%和2.4%)和形变却很小。若要令两个信号同步进入t-信道，只需撤掉光栅激光的后向分量使其由驻波模式转化为行波模式来同时获得两个高透射带即可。

如果两个不同频率的信号光在时间和空间上完全分离，又能在很短时间内通过动态调控行波耦合激光与驻波光栅激光来移动高反射带和高透射带的位置，使它们的绝大部分载频在不同时刻落入不同的高反射带或高透射带，还可令这两个不再同步的信号光全都进入r-信道或t-信道。这一全光路由控制方案由于可同时对两个信号进行实时操控，而比之前仅适用于单个信号处理的全光路由控制方案更具实用价值。

上述全光路由控制方案的主要缺点是：对同时到达节点B的两个不同频率信号光，无法使它们同时被反射进入r-信道。为了克服这一困难，需要设法在探测跃迁上同时建立两个(对应高反射率的)光子带隙，这可通过将耦合激光由行波模式转换为驻波模式得以实现。本文的第三部分将通过数值模拟论证这一设想是否可行。

3 两个高反射带的同时建立

还是考虑如图1所示的四能级Tripod型原子系统，只是令耦合激光ωc和光栅激光ωc同时具有驻波模式，空间周期分别为 ac=λc/［cos(α/2)］和 ag=λg/［cos(β/2)］，并具有不同的初始相位Φc和Φg(注：只有一个相干激光为驻波时无需考虑初始相位)。α(β)表示耦合(光栅)激光的稍微偏离z方向的前向分量和后向分量之间的夹角。

在考虑了上面几个因素后，利用与第二部分基本相同的数学方法，可方便地求得Tripod型超冷铷原子的光子带隙结构和反射光谱与透射光谱。这里，由于两个驻波的空间周期不尽相同，探测光经历的将不再是周期的Bragg散射，而是准周期的Bragg散射。于是，当两个驻波的初始相位或空间周期发生变化时，光子带隙结构会受到影响。在理想情况下，两个驻波的空间周期完全相同(ac=ag)，准周期结构退化为周期结构。此时，可在探测跃迁的不同频率处建立两个邻近的光子带隙，其反射率均达到了95%，如图5所示。这个双光子带隙结构的位置和宽度可通过改变两个驻波激光的强度和频率进行调控。

图5 两个驻波相干激光产生的双光子带隙结构Fig.5 A double photonic band-gap structure

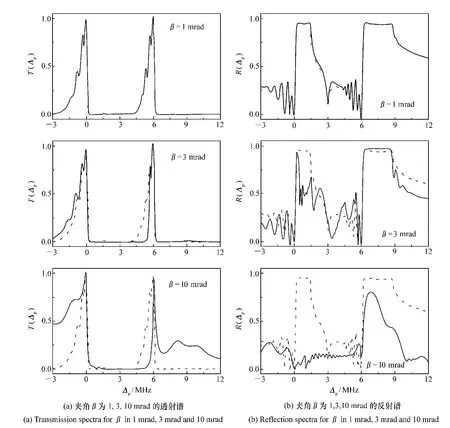
图6 一个驻波前向和后向分量间的夹角逐渐变化时介质的稳态光谱Fig.6 Steady spectra of the medium for a gradually increased angle between forward and backward components of one standing-wave field

因为上述空间准周期结构是由两个驻波激光叠加而成的，所以两个驻波的相对相位δ=Φg-Φc也会对双光子带隙结构有重要影响，如图7所示(虚线表示两个驻波激光的相对相位为零时的理想情况)。当δ很小时，双光子带隙结构与理想情况几乎相同，接近完美。当δ变得越来越大时，双光子带隙结构逐渐变形，直至被完全破坏，这与参数g逐渐增加时双光子带隙结构的变化情况类似。这是因为g或δ的增加导致两个驻波的波节和波腹在空间上逐渐分离，使得空间周期性越来越差。

图7 两个驻波的相对相位逐渐增加时介质的稳态光谱Fig.7 Steay spectra of the medium for a gradually increased relative phase between two standing-wave fields

以上结果是在两个驻波激光的失谐相差不大的情况下获得的，因此两个驻波激光相互影响很严重，并使得介质的稳态光学特性对有关参数十分敏感。如果两个驻波激光的失谐相差非常大(例如Δc-Δg=100 MHz)，两者的相互影响将非常微弱，以至于在探测跃迁附近相距很远的两个光子带隙对驻波激光的初始相位和周期差异不再敏感。因此，为了在探测跃迁上获得一个稳定的双光子带隙结构，需要令两个驻波激光的失谐相差较大。显然，一个稳定的双光子带隙结构可用来控制两个弱光信号，使它们同时发生完美反射，从而进一步丰富在第二部分描述的全光路由控制方案的信息处理功能。

4 结论

本文通过分析两个相干激光(或具有行波模式或具有驻波模式)与一个四能级Tripod型超冷铷原子系综的共振相互作用，提出了一个以相干诱导高透射带和高反射带为工作基础的全光路由控制方案。首先，利用行波耦合激光和驻波光栅激光导致的量子相干效应，在探测跃迁上同时产生了一个透射率约95%的频带和一个反射率约95%的频带。对这样的相干诱导高透射带和高反射带进行实时动态调控，可根据需要引导两个弱光信号的空间传输，使其中一个进入透射通道而另一个进入反射通道。然后，简单地撤掉光栅激光的后向分量，使它由驻波模式退化为行波模式，在探测跃迁上可同时得到两个透射率高达95%的频带，从而引导两个弱光信号同时进入透射通道。最后，若将耦合激光由行波模式转化为驻波模式，在探测跃迁上可同时产生两个反射率高达95%的频带，从而引导两个弱光信号同时进入反射通道。值得一提的是，无论是进入透射通道的信号还是进入反射通道的信号，均具有很小的形状变化和能量损耗，这对量子信息处理领域内微弱信号的全光路由控制是极为重要的。

［1］ STEANE A.Quantum computing［J］.Rep．Prog．Phys.，1998，61：117-173.

［2］ KIMBLE H J.The quantum internet［J］.Nature，2008，453：1023-1030.

［3］ FLEISCHHAUER M，LUKIN M D.Dark-state polaritons in electromagnetically induced transparency［J］.Phys．Rev．Lett.，2000，84：5094-5097.

［4］ LIU C，DUTTON Z，BEHROOZI C H，et al.Observation of coherent optical information storage in an atomic medium using halted light pulses［J］.Nature，2001，409：490-493.

［5］ OTTAVIANI C，VITALI D，ARTONI M，et al..Polarization qubit phase gate in driven atomic media［J］.Phys．Rev．Lett.，2004，90：197902.

［6］ APPEL J，FIGUEROA E，KORYSTOV D，et al..Quantum Memory for squeezed light［J］.Phys．Rev．Lett.，2008，100：093602.

［7］ HAM B S.Experimental demonstration of all-optical 1*2 quantum routing［J］.Appl．Phys．Lett．，2004，85：893-895.

［8］ VEWINGER F，APPEL J，FIGUEROA E，et al.Adiabatic frequency conversion of optical information in atomic vapor［J］.Opt．Lett．，2007，32：2771-2773.

［9］ WANG H H，LI A J，DU D M，et al..All-optical routing by light storage in a Pr3+∶Y2SiO4crystal［J］.Appl．Phys．Lett.，2008，93：221112.

［10］ GAO J W，WU J H，BA N，et al..Efficient all-optical routing using dynamically induced transparency windows and photonic band gaps［J］.Phys．Rev．A，2010，81：013804.

［11］ SAKODA K.Optical Properties of Photonic Crystals［M］.Berlin：Springer-verlag，2001.

［12］ YABLONOVITCH E.Inhibited spontaneous emission in solid-state physics and electronics［J］.Phys．Rev．Lett.，1987，58：2059-2062.

［13］ ARTONI M，LAROCCA G C，BASSANI F.Resonantly absorbing one-dimensional photonic crystals［J］.Phys．Rev．E，2005，72：046604.

［14］ ARTONI M，LAROCCA G C.Optically tunable photonic stop bands in homogeneous absor-bing media［J］.Phys．Rev．Lett.，2006，96：073905.

［15］ CUI C L，WU J H，GAO J W，et al..Double photonic band-gaps dynamically induced in a tripod system of cold atoms［J］.Opt．Express，2010，18：4538-4546.