基于大系统理论的随机需求条件下的生产—定位—路径集成研究

蔡洪文,张殿业,蔡洪武

(1.西南交通大学 a.经济管理学院,b.交通运输学院,四川 成都 610031;2.贵州警官职业学院,贵州 贵阳 550005;3.华能贵诚信托有限公司,贵州 贵阳 550002)

●营销管理

基于大系统理论的随机需求条件下的生产—定位—路径集成研究

蔡洪文1a,2,张殿业1b,蔡洪武3

(1.西南交通大学 a.经济管理学院,b.交通运输学院,四川 成都 610031;2.贵州警官职业学院,贵州 贵阳 550005;3.华能贵诚信托有限公司,贵州 贵阳 550002)

文章在一个由一个生产厂商、多个潜在设施 (配送中心)和多个客户组成的复杂大系统中,研究了随机需求条件下生产批量、配送中心定位和车辆运输路径问题的集成问题。为了解决复杂大系统所具有复杂性,把复杂大系统分解成了生产、配送中心和定位 -路径等三个相对独立的子系统是可行的办法。基于次梯度优化算法提出了一种优化协调机制,实现了系统的整体优化.最后,还给出了一个简单的算例。

供应链;随机需求;生产 -定位 -路径问题 (PLRP);大系统;分解协调

一、引 言

在物流供应链的研究中,生产批量问题、设施定位问题和车辆运输路径问题是广大学者研究的热点问题,这些学者中有的对这些问题的一个或几个问题分别从实用性、可操作性、随机性和模糊性等方面进行深入研究,如生产问题[1]和车辆路径问题[2]等,也有的把上述问题中的问题组合进行集成研究,如集成定位 -分配问题 (Location Allocation Problem,LAP)和车辆运输路径问题 (Vechile Routing problem,VRP)两个问题的定位 -路径问题 (LRP)[3-9]。集成生产批量、设施定位和车辆运输路径问题的研究在有关文献中尚未发现。在物流供应链研究中,集成研究生产批量、设施定位和车辆运输路径问题将是十分有意义的工作。

本文研究了一个工厂在潜在设施 (主要是配送中心)和随机需求的顾客都较多的情况下构成的供应链,在这个供应链里涉及到生产批量问题、设施 (主要是配送中心)定位问题和车辆路径问题。通过对这个复杂大系统的研究并为此建立了相应的数学模型,由于这是一个复杂大系统,求解比较困难,为此,我们借助大系统理论将上述问题分解成生产、配送中心和定位路径问题等三个问题并用分解协调的方法求解问题,最后通过实例验证了结论。

二、生产—定位—路径问题的数学模型

(一)建立模型的基本假设

(1)系统是一个工厂在潜在设施 (主要是配送中心)和随机需求的顾客都较多的情况下构成的供应链;

(2)系统考虑的成本有:①在工厂生产产品的过程中发生的固定的准备成本、可变的生产成本和库存的持有成本;②建造和启用潜在配送中心的固定成本;③潜在设施为了保证客户需求而准备的存货所发生库存持有成本;④从工厂运送工厂生产的产品到潜在设施的运送成本;⑤从配送设施把工厂生产的产品运送到每个客户的运送成本;

(3)产品生产不考虑提前时间,从工厂到潜在设施和设施到客户的进行货物运送时间也不考虑;

(4)一辆车辆可以重复运输或者多辆车辆可以并行运输以满足从工厂有大量的产品需要运输到潜在设施的要求;

(5)每个客户在接收由配送设施运送来的产品时只能有同一车辆提供服务;

(6)在每条巡回运输线路上只有一辆车辆为每个客户提供从配送设施把产品运送给客户的运输服务;

(7)车辆的运输能力不能低于每条巡回运输线路上客户的总需求;

(8)每辆运输的车辆在完成过程后返应返回到原来的出发点;

(9)所有的提供运输服务的车辆都是相同的型号。

集合:

j:配送设施的编号,j=1,2,...,J;

k:客户编号,k=1,2,...,K;

b:车辆编号,m=1,2,...,B;

t:时间阶段编号,t=1,2,...,T。

参数:

M:一个正数,其值可以足够大,在选择这个正数的值时可以考虑需求总量;

cht:在工厂为了保证客户和潜在设施的随机需求而准备的库存产品所发生的库存持有成本;

cpt:在工厂为了满足客户和潜在设施的需求所生产产品的单位生产成本;

cst:在工厂为了满足客户和潜在设施的需求所生产产品所发生的固定准备成本;

chjt:在潜在设施 j为了保证客户的需求保持合理库存而发生的库存持有成本;

ctjt:从工厂把工厂生产的产品运送到潜在设施 j所发生的产品单位运费;

Lj:从工厂把工厂生产的产品运送到潜在设施 j的运输距离;

ctjkt:从设施把工厂生产的产品运送到客户 k的单位运费;

Ljk:设施 j把工厂生产的产品运送到客户 k所产生的距离;

Djkt:在阶段 t潜在设施把从工厂购进的产品销售给客户k的所有产品中 i产品数量 (随机参数);

Fj:为了满足配送的需要而修建或使用潜在设施所发生的费用,假设修建的费用等于启用的费用相同;

at:工厂生产产品所拥有的生产资源;

Ct:工厂生产产品时制约工厂生产能力的因素;

Vb:从事产品运输的运输车辆在运输产品方面的能力;决策变量

It:在阶段 t为了满足客户和潜在设施的需求工厂准备的产品库存持有数量;并假设 I0=0;

Pt:在阶段 t为了满足客户和潜在设施的需求工厂进行生产的产品生产数量;

δt:阶段 t工厂是否进行产品生产,如果进行生产δit=1,否则δit=0;

Ijt:在阶段 t潜在设施 j为了满足客户需求而准备的产品的库存拥有数量,Ij0=0;

Zjt:阶段 t潜在设施是否被修建或启用,如果修建或启用潜在设施,则 Zjt=1,否则 Zjt=0;

Tjt:在阶段 t从工厂把工厂生产的产品从工厂运输到启用的设施 j的产品数量;

Qjt:在阶段 t启用的设施 j为了满足客户的需求向工厂订购产品数量;

Xjkbt:在阶段 t运输车辆 b从设施 j是否把从工厂购进的产品运送给客户 k,如果进行运送 Xijkt=1,否则 Xijkt=0;

Wjkt:如果由设施 j把从工厂购进的产品向客户 k供应产品,则 Wjkt=1,否则 Wjkt=0。

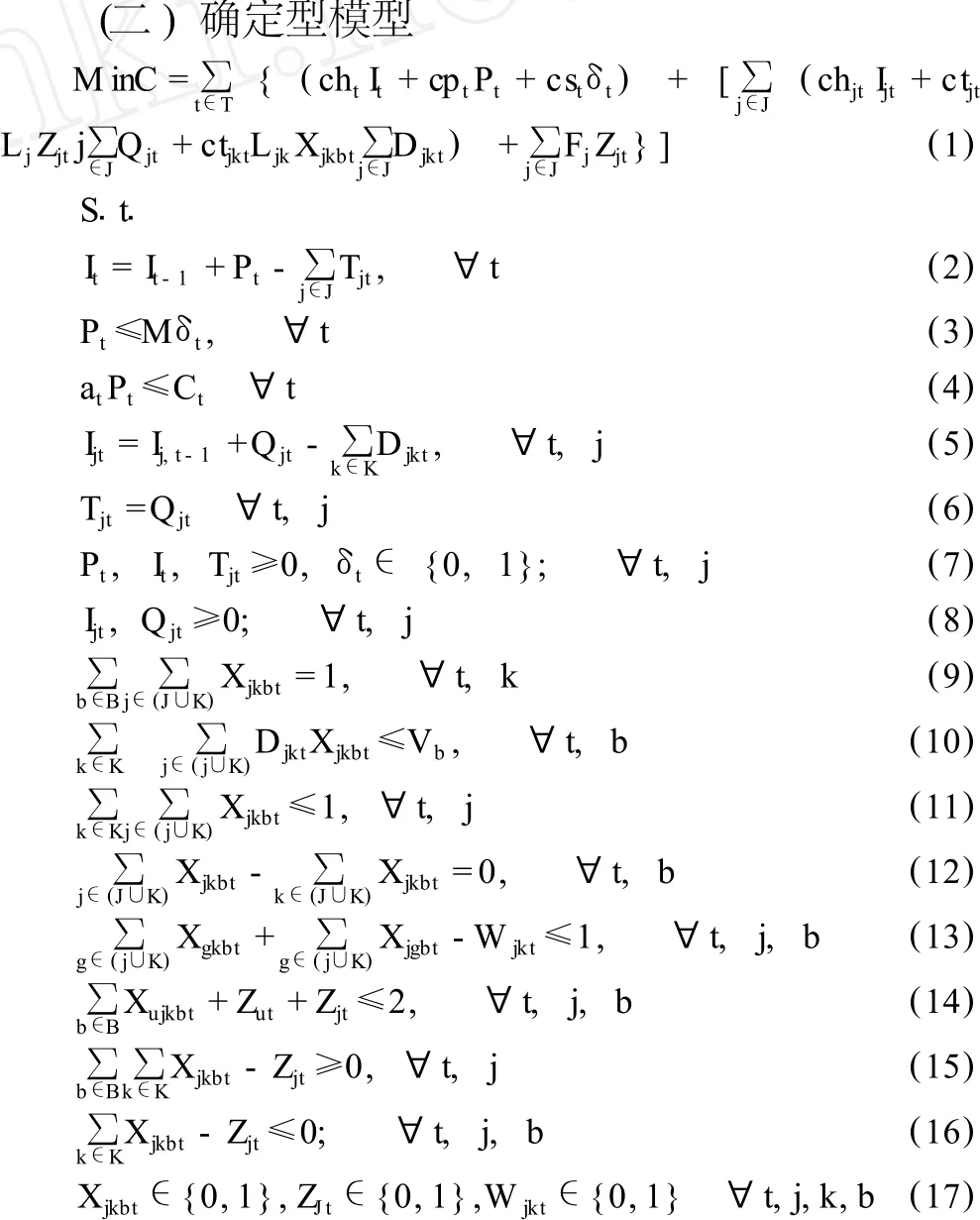
目标函数 (1)式表示生产产品的生产成本、库存持有成本和准备成本、建造或使用潜在设施的费用、设施为满足客户的需求而准备的库存所发生的成本、从工厂把工厂生产的产品运送到设施进行运输所发生的成本和设施把从工厂购来的产品运送给客户进行运输所产生的成本;约束条件 (2)为工厂本期库存等于上期库存加上本期生产量减去发往各设施的数量;(3)式表示工厂的生产量不大于需求量;(4)为工厂生产所需产能小于实际产能的限制;(5)为设施的本期库存等于上期库存加上本期订购数量减去发往各客户的数量;(6)式表示工厂的平衡约束和配送中心订货,式 (7)、(8)分别为工厂决策变量和设施决策变量不小于零,其中,生产准备变量是一个 0-1变量; (9)式保证每个客户只能在从设施把工厂生产的产品运送到每个客户的运输环线上;(10)保证车辆的运输能力不低于在每条巡回路上的货车运量;(11)式表示每辆车最多只能从一个设施或配送中心出发;(12)表示运输车辆将工厂生产的产品运送到某站点时,车辆的离开地点必须是该站点; (13)式表示每个站点都有且只有一辆运输车辆经过; (14)表示任意两配送设施之间在产品运输上没有任何联系;式 (15)、(16)表示任何一辆运输车辆只能将一个配送中心作为自己的起点; (17)表示三个变量为 0-1变量。

(三)随机需求下的数学模型

由于客户需求是随机的,也就是设施运送给各客户的数量 Djkt是一个随机参数,假定随机参数服从正态分布,Djkt～N (μjkt, σ2jkt)。为此对于原模型中的部分确定型约束条件可以转变成随机约束条件。

对于 (5)式,应当满足下列条件:

模型 (1)～ (17)为随机需求条件下的多周期的 0-1混合整数规划,该模型集成了生产批量、设施定位和车辆运输路径等三个问题。

三、基于大系统理论的分解协调过程

(一)分解过程

在随机需求的条件下,在一个融工厂生产问题、选址问题和配送路径问题集成的复杂大系统里,并且在这个复杂大系统里的个子系统存在耦合的情况下,可以运用大系统理论的有关知识把这个复杂大系统分解为两个相互独立而又相互协调的子系统——生产子系统和配送路径子系统。为了解决上述问题,我们可以运用拉格朗日松弛法进行求解。首先从(6)式可以看出,生问题产和配送路径问题之间存在耦合关系,为此我们引进拉格朗日 (Lagrange)乘子λjt≥0,将原问题分解成两个相对独立而又相互联系的生产子之问题和配送路径子问题:

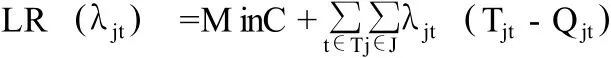
通过对问题进行计算,可得到工厂生产子问题和配送路径子问题:

工厂生产子问题 (Mp):

(二)协调过程

一个复杂大系统经过上述两次分解就变成了一个具有三级结构的供应链系统。其中,系统的第一级由定位路径问题(Mdl)和配送中心问题 (Mdc)等两个问题构成,其拉格朗日对偶问题为:

同时把原问题看做问题的第三级。

对于原来的复杂大系统通过运用大系统理论采用拉格朗日松弛法将问题分解为生产子问题、配送中心子问题和定位路径子问题等三个子问题,这三个问题相对独立而又相互协调。一个比较复杂的问题运用大系统理论分解协调理论得到比较满意的解决。

四、简单实例

假设有一个由一家工厂、三个潜在配送设施和十个终端客户组成的供应链系统,同时假设系统只有一种产品。在一个周期内工厂生产的产品都由配送设施通过运输车辆运送给客户 .十个客户的需求服从正态分布,即 Dj1～N (3,22),下面是有关参系数 (见表 1、表 3)。

表1 问题有关系数列表

用分支定界法求解配送中心子问题和生产子问题,用 C-W节约算法[9]和两阶段启发式算法[12]求解 LRP问题,其计算结果见表 3。

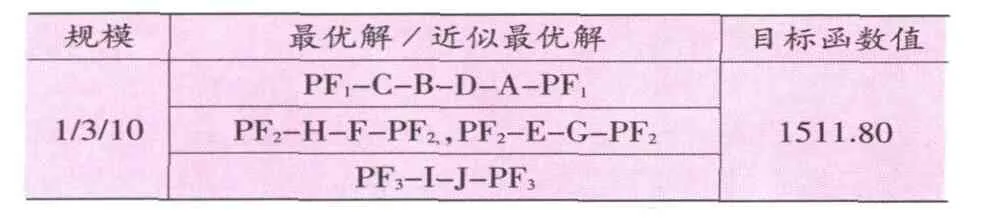
表3 计算结果

在一个周期生产一种产品的情况下,在一家工厂、三个潜在配送设施和十个终端客户组成的供应链系统中,配送设施 PF1的路径为 PF1-C-B-D-A-PF1;配送设施 PF2的路径为 PF2-H-F-PF2,,PF2-E-G-PF2;配送设施 PF3的路径为 PF3-I-J-PF3;问题的最小成本为 1511.80。

五、结 论

要解决一个集成生产、定位和运输路径等问题的大系统问题,可以运用大系统理论特别是拉格朗日松弛分解法把原问题分解成几个相互独立而又相互联系的子问题对问题进行求解。本文就是运用大系统理论的有关理论把原问题分解成的生产批量问题、配送中心问题和定位路径问题等三个相互独立而又相互协调的子问题后,采用分解协调理论较好的解决了这个问题.通过简单的实例验证了上述方法是可行的。

[1]David SL,Xin C,Julien B.The Logic ofLogistics:Theory,Algorithms,and Applications for Logistics and Supply chainManagement[M].Springer,2005.

[2]张建勇.模糊信息条件下车辆路经研究 [D].成都:西南交通大学,2004.

[3]Dilek T,Laura I B.Theory and Methodology:A twophase tabu search approach to location routingproblem [J].European Journal of Operation Research,1999,116:87-99.

[4]Hu Qinghe,Arun Kur mar,Zhang Shuang.A biding decision model in multiagent supply chain planning[J].International Journal of production research,2001,39 (15):3291-3301.

[5]Wu T H,Low C Y,BaiJW.Heuristic solutions tomultidepot location-routing problem [J].Computers&Operations Research,2002,29:1393-1415.

[6]Cappanera P,Gallo G,Maffioli F.Discrete facility location and routing of obnoxious activities[J].Discrete Applied Mathematics,2004,133:3-28.

[7]Daniela A,Maria G S.Distribution network design:New problems and related models[J].European Journal of Operation Research,2005,165:610-624.

[8]Nagy G,Salhi S.Location-routing: Issues,models and methods[J].European Journal of Operation Research,2007,177:650-672.

[9]张潜.物流配送路径优化调度建模与实务 [M].北京:中国物资出版社,2006:41-47.

[10]M·G·辛,A·铁脱里.大系统的最优化及控制[M].周斌,张国衡,王明良,译.北京:机械工业出版社,1983:107-108.

[11]刘宝碇,赵瑞清.随机规划与模糊规划 [M].北京:清华大学出版社,1998.

[12]李军,郭耀煌.物流配送 -车辆优化调度理论与方法[M].北京:中国物资出版社,2001.

[责任编辑:程 靖]

Study on Integrated Production-location-Routing Problem(PLRP)W ith Stochastic Demand Based on Large Scale System

CA IHong-wen1a,2,ZHANG Dian-ye1b,CA IHong-wu3
(1.a.School of Econom ics andManagement;b.School of Traffic and Transportation,Southwest Jiaotong University,Chengdu610031,China;2.Guizhou Police OfficerVocational College,Guiyang550005,China;3.Huaneng Guicheng Trust Corporation Lim ited,Guiyang550002,China)

Integrated production-lot-sizing,distribution-center-location and vechile routingwith stochastic demand were studied in a complex large scale system consisting of a factory,latentmulti-establishments(delivery center)and multi-customers.In order to resolve the complexity of the large scale system,a feasible method is that the largr scale system is decomposed into relatively independent production lot sizing subsystem,distribution center subsystem and location-routing subsystem.A coordination mechanis m based on subgradient optimization algorithm was presented,which achieves the globally optimized goal.Finally,an example for this problem was given.

supply chain;stochastic demand;production-location-routing problem (PLRP);large scale system;decomposition and coordination

F252

A

1007—5097(2011)03—0104—04

10.3969/j.issn.1007-5097.2011.03.025

2010—01—15

蔡洪文 (1969—),男,重庆铜梁人,博士研究生,研究方向:物流供应链管理;

张殿业 (1958—),男,辽宁鞍山人,教授,博士生导师,博士,研究方向:交通运输管理,物流管理;

蔡洪武 (1974—),男,重庆铜梁人,硕士,研究方向:物流供应链管理,财务管理。