Leslie人口年龄结构模型的修正
2011-11-02时书丽窦春轶
张 良, 时书丽, 窦春轶
(1.沈阳大学理学院,沈阳 110044; 2.辽宁大学信息科学与技术学院,沈阳 110036)
Leslie人口年龄结构模型的修正
张 良1, 时书丽2, 窦春轶2
(1.沈阳大学理学院,沈阳 110044; 2.辽宁大学信息科学与技术学院,沈阳 110036)
Leslie人口年龄结构数学模型建立在没有人口流动的基础上,本文试图建立含人口迁徙因素在内的修正模型,并研究修正模型年龄结构的稳定性.
年龄结构;Leslie矩阵;特征根;特征向量;幂法
1 Leslie年龄结构模型回顾
二十世纪四十年代末,Leslie建立了在与外界隔绝的封闭系统内,通过初始人口的数量及其年龄分布预测该系统未来某时刻人口的数量及年龄分布的数学模型[1-3].
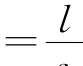
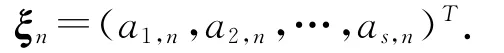
不妨假设下列的数据bk,d k(k=1,2,…,s)及mk(k=1,2,…,s-1)可根据统计资料得到:
bk为在单位时间段T内第i个年龄分类平均每个女性所生殖的后代数量;
d k为第k个年龄分类人口中女性所占比例;
mk为第k个年龄分类能活过单位时间段T而变成第k+1年龄分类的比例.
显然bk≥0,0≤d k≤1,k=1,2,…,s;0<mk≤1,k=1,2,…,s-1.
于是可以导出下列关系式:
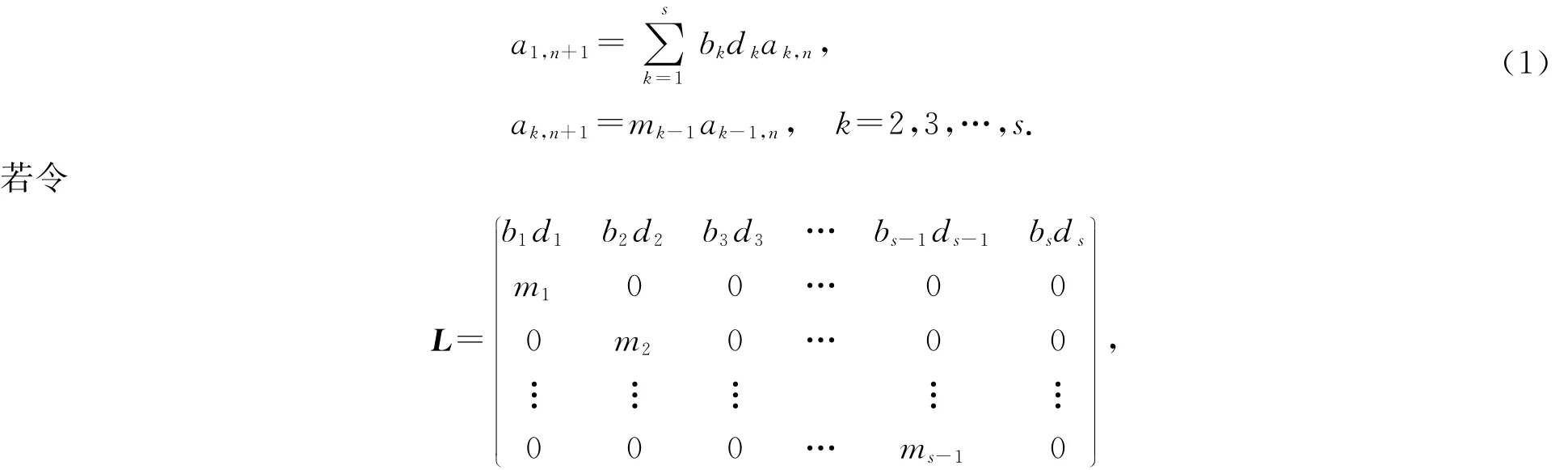
称其为Leslie矩阵,则(1)式可用矩阵表示为

如果当前的年龄结构向量ξ0为已知,则由(2)式,就得到Leslie年龄结构模型:

2 Leslie年龄结构模型的修正
现今世界人口流动频繁,几乎找不到与外界隔绝的封闭地域.所以有必要对Leslie年龄结构模型进行修正.
假设
αk表示由系统外进入该系统第k年龄分类的人数占第k年龄分类的人口总数的比例;
βk表示退出该系统而进入其它系统年龄属于第k年龄分类的人数占第k年龄分类的人口总数的比例.
不妨设
(i)0≤αk,βk<1,k=1,2,…,s;
(ii)在该系统生育的属于第一年龄分类小孩总是随其母亲进入或退出系统.
于是
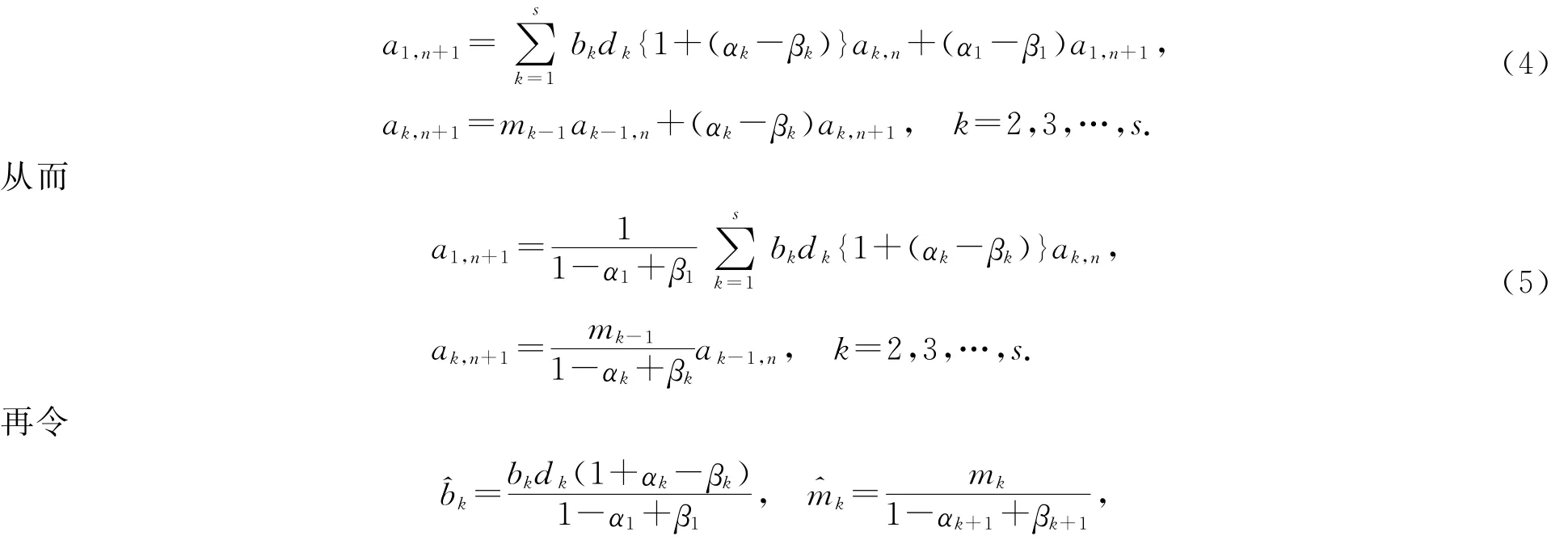
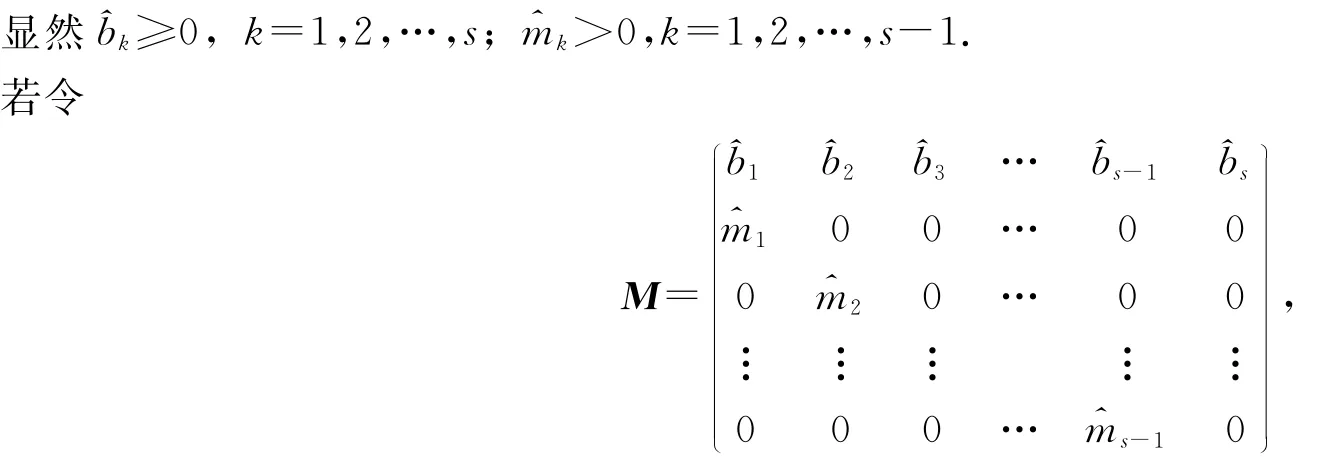
称M为Leslie的修正矩阵,于是(5)式可用矩阵表示为

从而得到Leslie年龄结构的修正模型:

3 年龄结构的稳定性
当n很大时,向量Mnξ0将如何变化?即修正模型年龄结构的稳定性[4-5].下面我们借助线性代数与矩阵计算方法来研究它[6-10].
设矩阵M的特征方程f(λ)=det(λI-M)=0,将行列式det(λI-M)按第一行展开后整理得

若λ≠0,则特征方程可变形为
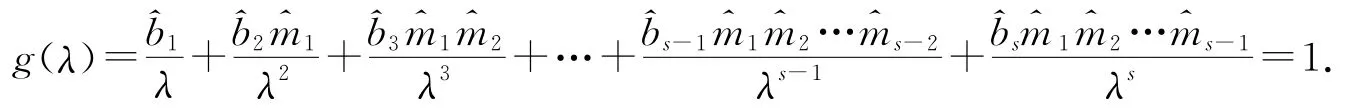

矛盾.所以矩阵M有唯一占优特征根.
定理2修正矩阵M有严格占优特征根.
证由定理1知M有唯一占优特征根λ0,对M的任意其它特征根λ,则|λ|≤λ0.若|λ|=λ0,由于M的第一行中必有两个相邻的元素^b i与^b i+1不为零(只要时间段——期的取法适当,所有相邻的年龄分类的女性不可能都不生育或者都是男性),因此
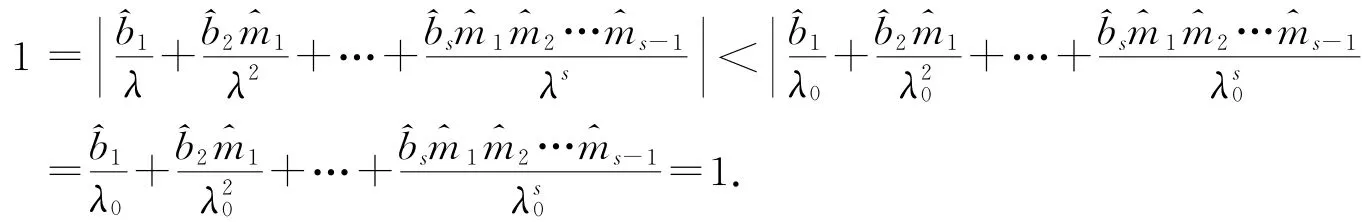
矛盾,因此|λ|<λ0.
对于修正矩阵M的严格占优特征根λ0及对应的特征向量x0,可采用矩阵计算之幂法求得:
设M的特征根λi(i=0,1,2,,…,s-1)满足条件
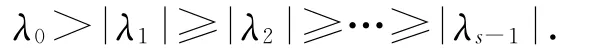
它们对应的特征向量依次是x0,x1,x2,…,x s-1,并且假定它们线性无关.其中λ0是M的严格占优特征根.

于是当α0≠0,k充分大时,

注 (i)若α0=0,可更换初始非零向量v0,再迭代;
(ii)在迭代过程中u k除max(u k)是为了避免计算λk0出现溢出现象.
4 结 论
因此我们得到下面诸结论:
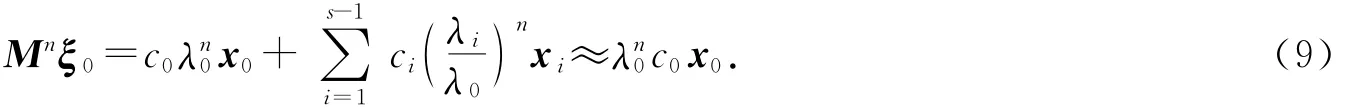
这表明当n充分大时,人口年龄结构按比例稳定在M的唯一的严格占优特征根λ0所对应的正的特征向量x0上,而与初始年龄结构ξ0无关.而且通过式(8)可以计算出λ0与x0的近似值.
2.年龄结构是以修正矩阵M的唯一严格占优特征根λ0之速率增长.当λ0<1时,人口数量逐渐减少;λ0=1,人口数量稳定;λ0>1,人口数量逐渐增加.

4.上面的结论与方法完全适用于动物、昆虫等.
[1]Leslie P H.On the use of matrices in certain population mathematics[J].Biometrika,1945,20(3):156-168.
[2]姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2004.
[3]Lucas W F.生命科学模型[M].翟晓燕等,译.长沙:国防科技大学出版社,1986.
[4]Castro ML,Sliva J A L,Justo D A R.Stability in an age-structured metapopulation model[J].Journal of Mathematical Biology,2006,52(2):183-208.
[5]Anatoli V S,Frank C.Models in Population Biology[M].New York:Springer,2002.
[6]许世壁.谈研究年龄结构之数学模型[J].数学传播,1983,7(3):8-10.
[7]蒋尔雄,高坤敏,吴景琨.线性代数[M].北京:人民教育出版社,1978.
[8]蒋正新,施国梁.矩阵理论及其应用[M].北京:北京航空学院出版社,1988.
[9]刘玲,葛福生.数值计算方法[M].北京:科学出版社,2005.
[10]刘文瑜,杜基奎,陈金山.计算方法[M].北京:科学出版社,2007.
Adjusting Leslie’s Model of Population Age Structure
ZHANGLiang1,SHIShu-li2,DOUChun-yi2
(1.College of Sciences,Shenyang University,Shengyang 110044,China;2.College of the Information Science and Technology,Liaoning University,Shenyang 110036,China)
Leslie established mathematical model of population age structure under the condition of without migration.To correct its defect,an adjusting model with migration is set up and studied its age structure stability.
age structure;Leslie’s matrix;eigenvalue;eigenvector;power method
O29;C92-03
A
1672-1454(2011)04-0099-04
2008-09-28;[修改日期]2008-12-09
