与给定多边形相切的可调广义Ball闭曲线

高 健， 刘 植

（1.安徽医科大学卫生管理学院，合肥 230032； 2.合肥工业大学数学学院，合肥 230009）

与给定多边形相切的可调广义Ball闭曲线

高 健1， 刘 植2

（1.安徽医科大学卫生管理学院，合肥 230032； 2.合肥工业大学数学学院，合肥 230009）

讨论了与给定控制多边形相切的分段三次、五次和六次可调广义Ball曲线的构造方法，所构造的曲线分别是C1，C2和C3连续的，而且对切线多边形是保形的.曲线上的所有广义Ball曲线段的控制点由切线多边形的顶点直接计算产生.给出了在保持公共连接点处相应连续的情况下，内控制点的活动范围.曲线可以在一定范围内做局部修改.计算实例表明使用本文的方法灵活、方便、有效.

广义Ball曲线；切线多边形；保形曲线

1 引 言

在CAGD及实际应用中人们发现广义Ball曲线类似于Bézier曲线，有很好的保形性质，且在某些方面，有比Bézier曲线更好的性质［1］.例如：广义Ball曲线的赋值算法具有稳定的递归算法，且2m＋1次广义Ball曲线的赋值只需2（m＋1）2次乘法和（m＋1）2次加法，而同次数的Bézier曲线需要2（m＋1）（2m＋1）乘法和（m＋1）（2m＋1）次加法（de Casteljau算法）.因此，Bézier曲线绘图如先转化为广义Ball曲线再绘图，无疑可以大大减少计算量；又如，广义Ball曲线退化为低一阶曲线的充要条件是中间两个控制点重合，因此很容易判断，而Bézier曲线的退化条件就要复杂得多；此外，广义Ball曲线升阶可以两次两次进行，其计算量只是同次数Bézier曲线升阶的一半.因此，在外形设计中，广义Ball曲线越来越受到重视，有着广泛的应用价值 .

在CAD，CAGD及逼近的设计过程中，通常会先根据尺寸要求确定控制点，再根据控制点用直线段绘制样片的大体轮廓，即控制多边形，在多边形内用直线和曲线绘制封闭的图形.由于样片的形状不规则，即构成样片的曲线比较复杂，为了使曲线光顺、有弹性，且易于修改，经常会遇到曲线与控制多边形相切的问题.构造与给定控制多边形相切的曲线问题，已经有不少文章对之进行了详述的讨论，且在实践中得到了应用［2－8］.文［7，8］构造了C1，C2和C3连续的广义Ball曲线，但其中C1和C2连续的曲线只能通过调节切点的位置进行局部修改，从而降低了局部修改的灵活性，且C3连续的广义Ball曲线是唯一确定的，不可能做局部修改.本文主要研究了与给定多边形相切的广义Ball曲线，基于构造组合曲线的可控性，给出更加灵活的构造方法.所构造的C1，C2连续的广义Ball曲线除了可以调节切点位置外还可以通过调节其内控制点参数对曲线做局部修改，使得曲线的局部修改更加灵活、方便、有效.且本文构造的C3连续的广义Ball曲线的局部修改也是简单方便的.计算实例表明本文的方法是可行的.

2 与给定多边形相切的C1可调广义Ball闭曲线

对于给定的闭的多边形〈V0，V1，…，V n〉，其中V n＝V0.假设待构造的分段三次广义Ball曲线在切线多边形的第i条边V i V i＋1上的切点为

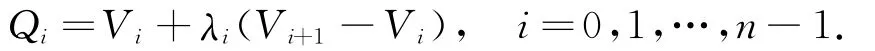
本节目的是希望在每相邻两切点Qi，Qi＋1之间构造一段三次广义Ball曲线ri（t）（i＝0，1，…，n－1），其相应的控制点选取为

其中切点调节参数αi＜λi＜1－αi.αi为内控制点的调节参数，它满足

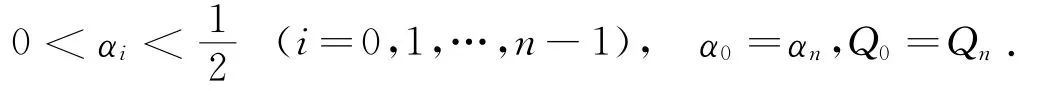
相应的三次广义Ball曲线段为

由三次广义Ball曲线的端点性质［9］，则有

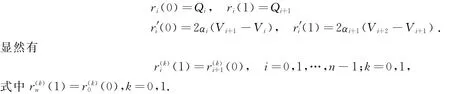
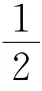
设V i＋1是切线多边形的转折点，即矢量V i－1V i×V i V i＋1与矢量V i V i＋1×V i＋1V i＋2方向相反，这时第i－1段与第i段曲线凸性相反，且在切点Qi处形成一个拐点，因此上面构造的分段三次广义Ball曲线拐点个数与切线多边形的转折点个数相等.即该曲线对其给定切线多边形是保形的.

由此可知，上面构造的分段三次可调广义Ball闭曲线是C1连续的，保形的且与每条边V i V i＋1相切.

例1给定平面上一非凸的切线六边形，用上述算法绘制与给定六边形每边相切三次广义Ball曲线的三个图形.图1中的图形分别是λi＝0.45，αi＝0.4；λi＝0.55，αi＝0.4；λi＝0.55，αi＝0.3.

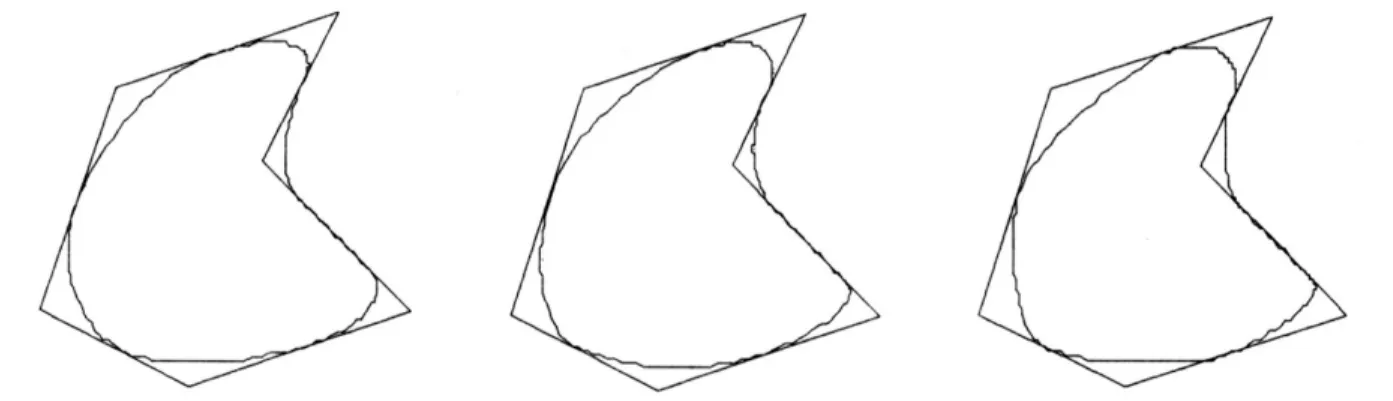
图1 λi，αi取不同值时的三次广义Ball曲线

综上可知，分段三次广义Ball曲线的形状由参数λi，αi的选取确定，曲线的切点在一定范围内可以任意选取.λi增大，切点Qi向V i＋1靠近；λi减小，切点Qi向V i靠近.αi在一定范围内增大时，内控制点向切线多边形的顶点靠近，生成的组合曲线相应的向切线多边形的顶点靠近，否则将远离顶点.

3 与给定切线多边形相切的C2可调广义Ball闭曲线

假设给定的闭的多边形〈V0，V1，…，V n〉，其中V n＝V0.待构造的分段五次广义Ball曲线在切线多边形的第i条边V i V i＋1上的切点为

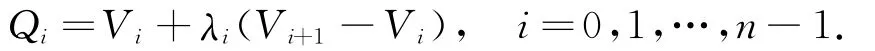
本节目的是希望在每相邻两切点Qi，Qi＋1之间构造一段五次广义Ball曲线ri（t）（i＝0，1，…，n－1），其相应的控制点选取为

相应的五次广义Ball曲线段为

由此可知，上面构造的分段五次可调广义Ball闭曲线是C2连续的，类似第一节的证明，可知构造的分段五次可调广义Ball闭曲线是保形的，且与每条边V i V i＋1相切.

例2给定平面上一非凸的切线七边形，用上述算法绘制与给定七边形每边相切五次广义Ball曲线的三个图形.图2中的图形分别是λi＝0.52，αi＝0.32；λi＝0.52，αi＝0.22；λi＝0.65，αi＝0.22

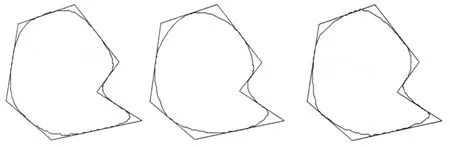
图2 λi，αi取不同值时的五次广义Ball曲线

综上可知，分段五次广义Ball曲线的形状由参数λi，αi的选取确定，曲线的切点在一定范围内可以任意选取.λi增大，切点Qi向V i＋1靠近；λi减小，切点Qi向V i靠近.αi在一定范围内增大时，内控制点向切线多边形的顶点靠近，生成的组合曲线相应的向切线多边形的顶点靠近，否则将远离顶点.

4 与给定切线多边形相切的C3可调广义Ball闭曲线

我们仍假设对于给定的闭的多边形〈V0，V1，…，V n〉，其中V n＝V0.待构造的分段六次广义Ball曲线在切线多边形的第i条边V i V i＋1上的切点为

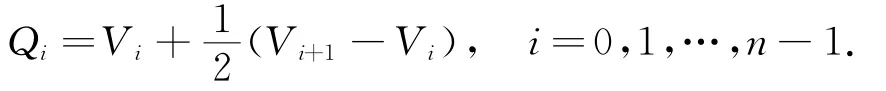
本节目的是希望在每相邻两切点Qi，Qi＋1之间构造一段六次广义Ball曲线ri（t）（i＝0，1，…，n－1），其相应的控制点选取为

其中αi为内控制点的调节参数，它满足

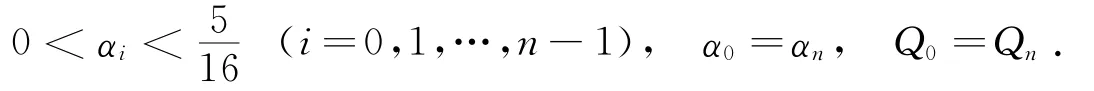
相应的六次广义Ball曲线段为

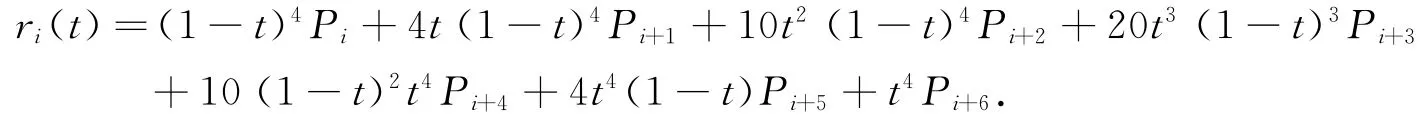
由六次广义Ball曲线的端点性质［9］，则有

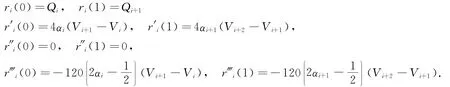
显然有

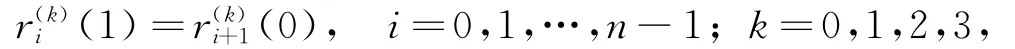
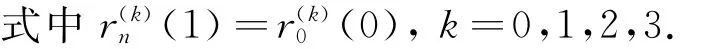
由此可知，上面构造的分段六次可调广义Ball闭曲线是C3连续的，类似前面证明，可知构造的分段六次可调广义Ball闭曲线是保形的，且与每条边V i V i＋1相切.

例3给定平面上一非凸的切线七边形，用上述算法绘制与给定七边形每边相切六次广义Ball曲线的三个图形.图3中的图形分别是αi＝0.1；αi＝0.2；αi＝0.3

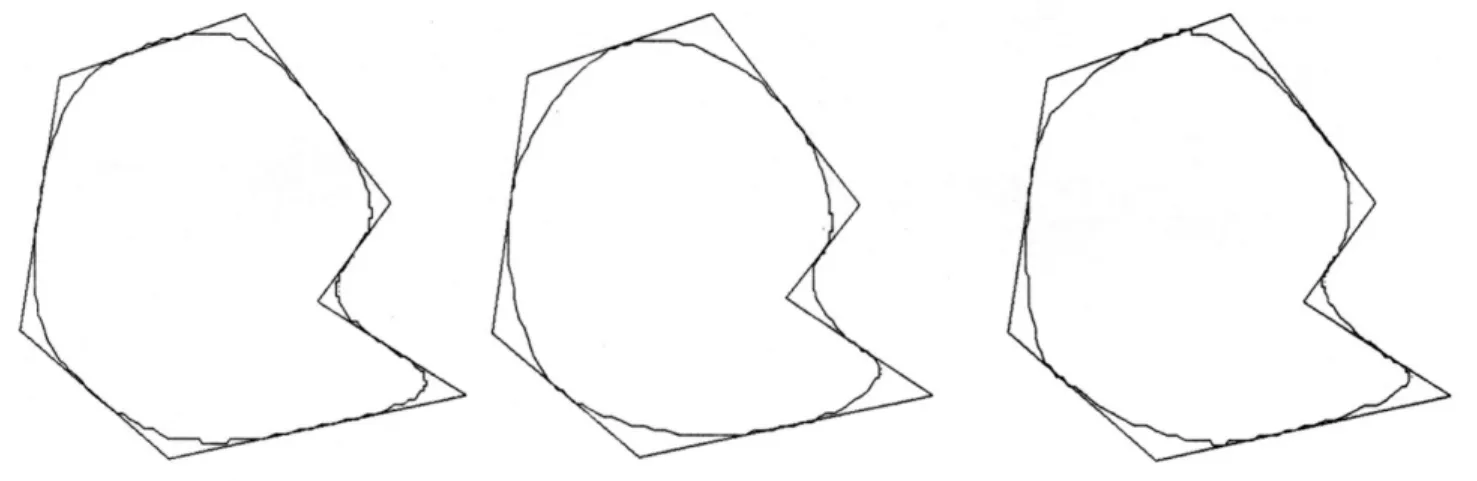
图3 αi取不同值时的六次广义Ball曲线

综上可知，分段六次广义Ball曲线的切点位置是确定的.曲线的形状由参数αi的选取确定.αi在一定范围内增大时，内控制点向切线多边形的顶点靠近，生成的组合曲线相应的向切线多边形的顶点靠近，否则将远离顶点.

5 结 论

用本文构造的与给定多边形每边相切的广义Ball曲线，与传统的方法相比，它具有以下优点：

（i）本文构造的曲线只要给定多边形以及各调节参数的值，即可构造曲线，无需额外信息，从而大大减少了计算量.

（ii）所构造的三次、五次和六次广义Ball曲线分别是C1，C2和C3连续的，光滑性好.

（iii）所构造的曲线不仅与给定多边形的每条边相切，而且对多边形具有保形性，避免了曲线产生多余的拐点.

（iv）可以在形状参数的取值范围内选择不同的参数值，进行曲线设计.无论是曲线内控制点的调整，还是切点控制参数的改变，都是对曲线具有局部性的，曲线修改十分方便.

［1］丁友东，李敏.广义Ball曲线的性质及应用［J］.应用数学学报，2000，23（4）：580－595.

［2］Hering L.Closed（C2＿andC3＿Continuous）Bézier and B－spline curve with given tangent polygons［J］.CAD，1983（1）：3－6.

［3］Fang K.Closed（G2＿Continuous）Bézier curve with given tangent polygon［J］.Chinese Journal of Numerical Mathematics，1991，3（2）：34－38.

［4］方逵，蔡放，谭建容.带有给定切线多边形的C2和C3Bézier闭样条曲线［J］.计算机辅助设计与图形学报，2000，12（5）：330－332.

［5］刘植.与给定切线多边形相切的C3Bézier可调闭样条曲线［J］.合肥工业大学学报，2005，28（5）：223－224.

［6］闫德勤.与给定多边形相切的四次可控C2Bézier曲线［J］.计算机应用与软件，2003，3（5）：52－64.

［7］王成伟姚云.与给定多边形相切的C1广义Ball闭曲线［J］.北京服装学院学报，2002，22（1）：71－74.

［8］王成伟.与给定多边形相切的C2和C3广义Ball闭曲线［J］.高等学校计算数学学报，2002，24（4）：349－354.

［9］王国瑾，汪国昭，郑建民.计算机辅助几何设计［M］.北京：高等教育出版社，2001：100－112.

Closed Adjustable Generalized Ball Curves with Given Tangent Polygon

GAOJian1，LIUZhi2
（1.Health Management College，Anhui Medical University，Hefei 230032，China；2.School of Mathematics，Hefei University of Technology，Hefei 230009，China）

This paper proposes an approach of constructing planar piecewise closed generalized Ball curve of 3th、5th and 6th degree with all edges tangent to a given control polygon and the curve segments can be joined together withC1，C2andC3continuity respectively.The control points of the generalized Ball curve segments are computed simply by the vertices of the given tangent polygon.The admissible scope of the inner control points is given in order to guarantee corresponding continuity.Local modifications for these curves are possible.The effectiveness as well as adaptability of the method is manifested by experimental results.

generalized Ball curve；tangent polygon；shape－preserving curve

TP241.3

A

1672－1454（2011）04－0042－05

?

2008－03－31