基于ANP的企业科技员工激励体系研究

黄焕宗

(黎明职业大学,福建 泉州 362000)

在科技创新能力已经成为一个国家和地区核心竞争力的今天,产学研的合作构成了创新体系的重要组成部分。通过科技人员服务企业,把知识、技术从大学、科研院所转移到企业内部并应用于价值创造,是企业提高创新能力,赢得竞争优势的重要途径,也是构建区域乃至国家创新体系的必要条件。在这个大背景下,深化科技人员服务企业的相关问题研究引起了很多学者的注意,在科技人员的激励因素、机制和产学研相关方面的利益分配模式、机制等方面产生了一大批有借鉴意义的研究成果。以科技人员的激励因素为例,王飞绒[1]通过对科技人员特征的总结,提出了包括自主环境的创造和多种激励方式组合等强化科技人员激励的5项对策。黄玲炜[2]从薪酬、股权、培训及企业文化等方面探讨了科技人员的激励机制构建。王伟强[3]则利用网络调查和问卷调查等调查工具,研究了激励科技人员的主要因素,即:薪酬福利、领导素质、个体发展、企业发展、公平公正。此外,国内外的许多组织和个人也就这个课题进行了深入调查研究[3]。综合来看,这些研究认为薪酬福利、发展空间、领导因素、公平情况等4个因素在企业科技员工的激励方面占据主导地位。但同时,也存在着一些值得再深入研究的问题。首先是激励因素的重要性问题,由于研究对象和研究方法的差异,不同的研究所获得的激励因素权重总是存在差异甚至大相径庭;其次是激励因素的可操作性问题,以往研究成果对激励因素的选择过于笼统,没有细化到具体的指标,这对于现实执行显然缺乏可操作性。

基于这个原因,一种定量和定性相结合,能体现科技人员激励因素中各指标间相互关系和各指标权重的研究方法将是科技人员激励机制研究的重要补充。本文利用网络层次分析法 (ANP)理论建立科技人员激励因素指标体系,并研究了在此基础上确定指标权重的方法。

1 科技人员激励因素研究

1.1 ANP方法简介

过去对一个系统进行综合评价、决策所建立的指标体系是递阶层次结构,而通过ANP方法,则可以扩展到网络结构。网络层次分析法 (AnalyticNetwork Process,ANP)是由Saaty教授1996年提出的,它提供了解决决策问题的一个总的框架。首先将系统元素划分为两大部分,第一部分称为控制因素层,包括问题目标及决策准则。所有的决策准则均认为是彼此独立的,且只受目标元素支配。控制因素中可以没有决策准则,但至少有一个目标,是典型的递阶层次结构。第二部分为网络层,它是由所有受控制层支配的元素组组成的,其内部是互相影响的网络结构[4]。

1.2 指标体系

以薪酬福利 (B)、发展空间 (C)、领导因素(D)、公平情况 (E)等四个因素为主指标,在此基础上细化出有利于具体操作的元素指标,构成指标体系 (图1)。

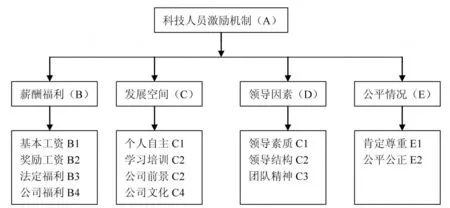
图1 科技人员激励因素指标体系

1.3 权重确立

1.3.1 因素影响分析 上述步骤建立了三层指标体系,这个体系包括了4个主要元素组,这些主要元素组之间及各子元素之间的关系都不是独立的,而是相互之间有依存关系和反作用关系。如领导因素影响薪酬福利,企业公平情况又必然反作用于发展空间。又如,团队精神决定了影响了公司文化等等。很明显,人为机械的把各个因素分离开来评分的评价方式不能全面的反映能够激励科技人员的因素所在。基于ANP方法可以建立这4个主因子元素组之间的网络关系,称为外部依赖关系,这种相互关联的结构更能反映出企业可持续发展因素之间的内在联系,具有系统性和科学性。主要指标间的相互关联关系可以用图2表示。

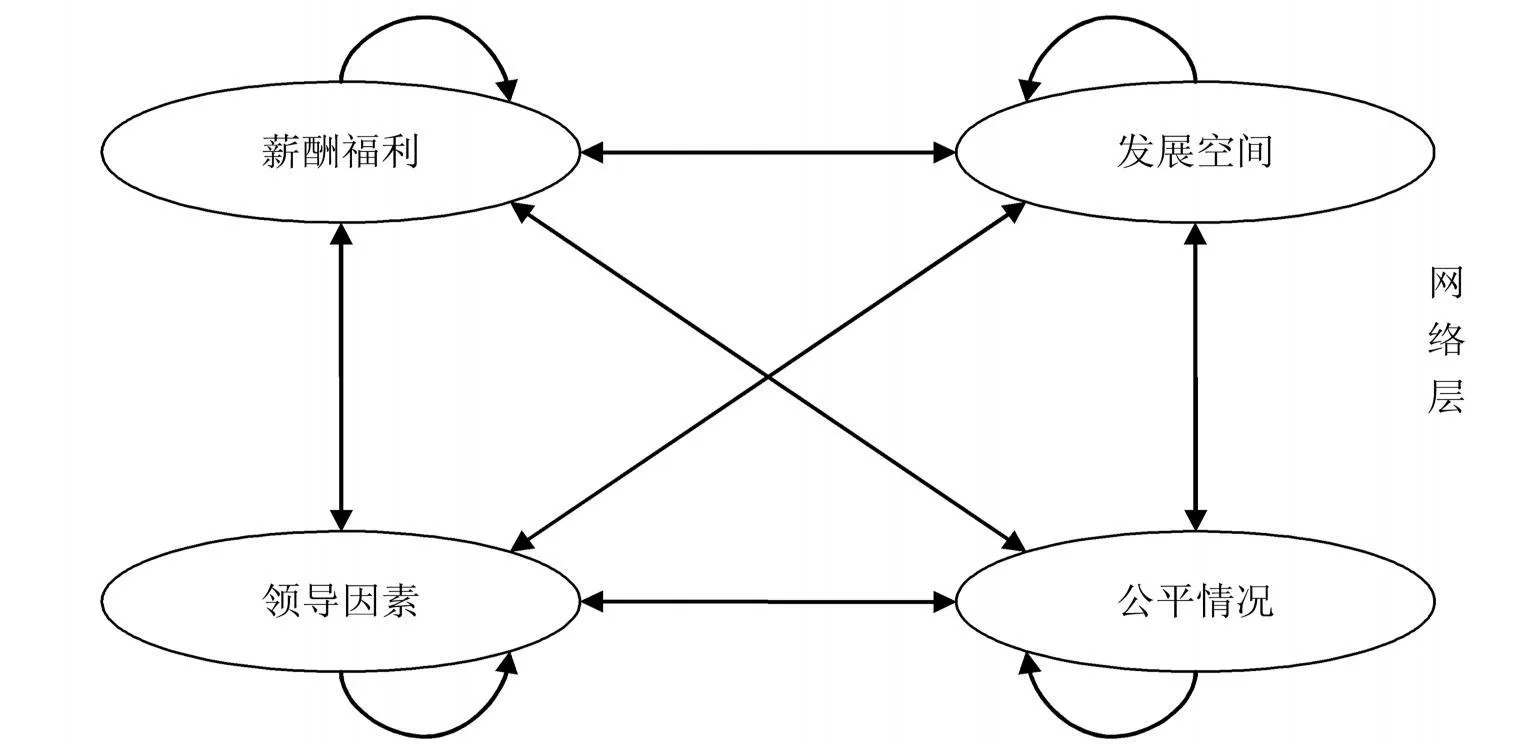
图2 科技人员激励主要指标影响网络图

而各个元素之间也存在相互影响关系,为研究方便,我们这样规定:假设在同一层次上有n个因素,对于给定的第i个因素和第j个因素作相互比较判断,对照表1所示“1～9标度”,便可以得到一个表示相对重要性的数字uij,uij的确定可通过专家评议或者小组讨论的方式确定。

1.3.2 因素权重的计算 在确定了科技人员激励因素指标元素影响关系uij之后,可以进行各因素权重的计算,其步骤如下[5]:

表1 1～9标度表

步骤1:超矩阵W的建立。设ANP的控制层中有元素p1,p2,…,p m,控制层下网络层有C1,C2,…,CN,其中Ci中有元素ei1,ei2,…,ein i,i=1,2,…,N。以控制层元素p s(s=1,2,…,m)为准则,以Cj中元素ejk(k=1,2,…,nj)为次准则,将元素组Ci中元素按其对ejk的影响力大小进行间接优势度比较,即在准则p s下构造判断矩阵:

并由特征根法得权重向量wi1(jk),wi2(jk),…,w ini(jk)。对于k=1,2…,ni重复上述步骤,得到式(1)所示矩阵Wij。

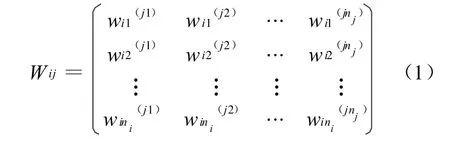
Wij的列向量指的是Ci中的元素ei1,ei2,…,eini对Cj中元素ej1,ej2,…,ejnj的影响程度所得到的排序向量。如果Cj中元素不受Ci中任何元素影响,则Wij=0。对于i=1,2,…,N;j=1,2,…,N的情况,重复上述步骤,最终可获得准则ps下的超矩阵W。

步骤2:权重向量的确定。在超矩阵W中,元素Wij反映元素i对元素j的一步优势度;还可以计算W2,其元素wij2表示元素i对元素j的二步优势度,W2仍然列为归一化矩阵,以此类推,可以计算W3,W4,…,当W∞存在时,W∞的第j列就是准则p s下网络层中各元素对于j的极限相对权重向量。即:

其中每一行的数值,即为相应元素的局部权重向量;当某一行全部为0时,则相应的局部权重为1。将局部权重按元素顺序排列即得到局部权重向量。

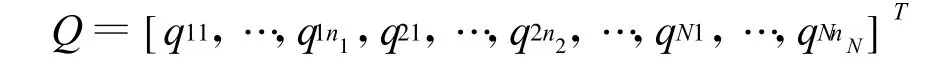
该运算的实现可以通过软件super decision来完成[6]。通过这个步骤得出了科技人员激励因素指标体系中各因素的排行情况,也就是在进行科技人员激励时各项政策实施的优先情况。

2 结论

本文提出用网络层次分析法方法建立科技人员激励因素评价体系和求解指标权重是一种新的尝试。通过研究,本文建立了科技人员激励因素的细化指标体系,并提出了权重的计算模型。根据这一模型,科技人员激励机制的研究理论得到进一步丰富,并可为决策部门提供参考。

[1]王飞绒.科技人员特征及其激励 [J].科技与管理,2003(5):121-125.

[2]黄玲炜.长沙矿冶研究院科技人员激励机制研究 [D].中南大学,2007.

[3]王伟强.知识员工激励因素的实证研究及中外比较分析[J].电子科技大学学报,2008,10(2):39-44.

[4]SAATY T L.Decision Making with Dependence and Feedback[M].Pittsburgh.PA:RWS,1996.

[5]王莲芬.网络分析法 (ANP)的理论和算法 [J].系统工程理论与实践,2001(3):44-50.

[6]刘睿,余建星,孙宏才,等.基于ANP的超级决策软件介绍及其应用 [J].系统工程理论与实践,2003(8):141-143.