联合风险投资合作伙伴的选择

王雷

（江南大学商学院，江苏无锡214122）

联合风险投资合作伙伴的选择

王雷

（江南大学商学院，江苏无锡214122）

合作伙伴选择是联合风险投资成功的关键环节。文章分析了主导型风险投资公司选择联合投资合作伙伴的影响因素，将粗糙集理论应用于指标的约简，建立了合作伙伴选择的评价指标体系；运用神经网络法建立合作伙伴选择的评价模型，为联合风险投资选择最佳合作伙伴。将粗糙集理论作为神经网络系统的预处理器，从中挖掘出反应评价指标本质关系的重要属性与伙伴选择知识规则，通过指标的约简提高了神经网络的收敛速度与选择的准确率。最后，实例验证表明，该方法是正确有效的。

风险投资；联合投资；粗糙集；神经网络模型；合作伙伴

0 引言

联合风险投资通过对创业企业进行权益投资而结成共享收益、共担风险、协同管理的利益共同体，是风险投资企业之间的一种战略联盟或动态联盟[1]。在联合风险投资联盟中，通过成员在资金、管理人才、信息、技术等方面的资源优势互补，不仅能够解决风险投资项目的巨额资金需求、分散项目风险，同时有利于减少投资中普遍存在的不对称信息问题，提高投资项目的成功率，因而在风险投资领域发挥着越来越重要的作用。在风险投资最为发达的美国，最高年份的风险投资行业有将近65%的交易都是采用联合投资完成的。据Zero2IPO清科公司的研究报告显示，在2001年中国新增加的风险投资项目中，有近40%的项目采用联合投资；2002年中国大陆地区有45.7%的风险投资项目采用了联合投资形式；2003年采取联合投资的项目所占的比例约占41.1%。

随着联合投资这种风险投资形式日益受到企业界和风险投资家的重视，合作伙伴的选择作为建立联合风险投资利益共同体的第一步，是联合风险投资动态战略联盟建立的基础和关键环节，慎重地选择合作对象将是这一特殊联盟顺利发展的前提条件，也是风险投资成功与否的关键因素。

目前，关于联盟合作伙伴评价与选择的主要方法有层次分析法、遗传算法、Agent法、证据推理法、模糊综合评判法以及神经网络法等。本文将粗糙集理论与神经网络相结合，应用于联合风险投资合作伙伴的选择。将粗糙集作为神经网络的预处理器，通过指标约过滤数据库中的冗余数据简压缩信息空间容量，简化训练集，极大地缩短了训练时间并提高神经网络的预测精确度[2]，为解决联合风险投资中合作伙伴的选择问题提供了一个新的视角。

1 联合风险投资合作伙伴选择影响因素与评价指标

1.1 联合风险投资合作伙伴选择的影响因素

表1 联合风险投资合作伙伴选择的影响因素及其描述

本文假设联合风险投资合作伙伴的选择将受到联合动机的影响。因此，联合投资合作伙伴选择将受到合作者财务状况、资源特征、投资风格、公司声誉等因素的影响，具体内容见表1所示。

1.2 基于粗糙集理论的联合风险投资合作伙伴选择评价指标体系的确立

（1）粗糙集理论确定评价指标的思想与步骤

粗糙集理论RST是波兰科学家Z.Pawlak教授在1982年提出的一种数据推理方法。它不需提供问题所需处理的数据集合之外的任何先验信息，仅根据观测数据删除冗余信息，分析不完整知识的程度—粗糙度—属性间的依赖性与重要性，生成分类或决策规则等。

粗糙集理论的基本定义为：四元组S={U,A,V,f}是一个知识系统，其中U表示对象的非空有限集合，称为论域，U={x1,x2,…,xn}；A=C∪D表示所有属性的非空有限集合，其中子集C是条件属性集，D={I}是决策属性集，其中Va是属性a的值域；f为一映射函数集，它确定对象的属性所对应的值，f={fi/U×A→Vi(i≤m)}。

粗糙集理论认为知识是基于对对象分类的能力，分类的过程是将相差不大的对象分为一类，它们的关系是不可分辨关系，也称等价关系。约简是能保证决策分类质量的最小属性集合，一族等价关系可能有多个约简；核是不能去除的最重要的属性集合，是构成任何一个约简的必须成分，全部约简的交集定义为核。决策表的属性核包含在所有约简中，所以找出属性核是约简计算的基础。目前，粗糙集理论已被成功地应用于机器学习、决策分析、过程控制、模式识别与数据挖掘等领域[3]。本文应用基于粗糙集理论和信息量的概念，构造决策系统的可辨识矩阵和分辨函数，通过分辨矩阵的启发式指标属性约简算法，进行指标优化，得到伙伴选择决策系统的核和约简，最终确立联合风险投资合作伙伴选择的评价指标体系。

（2）应用粗糙集理论确定评价指标

假设有n个愿意合作的风险投资构成合作伙伴候选集U={x1,x2,…,xn}；前文探讨了影响联合风险投资合作伙伴选择的主要因素，综合Saxton(1997)、Cravens(2003)的研究成果以及文献[4，5]分析，本文选取财务状况a、资源状况b、互补性c、声誉与信任d、投资风格e、发展战略f、综合实力g、投资阶段h共八个指标作为伙伴选择的初选评价指标，这些评价指标作为条件属性集C={a,b,c,d,e,f,g,h}；D={I}为伙伴选择决策属性集。合作伙伴选择的决策系统可表示为S=(U,C∪D)，且C∩D=ф。由于每个指标重要性不尽相同，并且有些指标可能存在相关性，而指标综合评价要求各指标之间应该极大不相关。因此，对相关性较大的指标有必要进行筛选和约简。

现取50组通过认定的数据作为学习样本U={x1,x2,…,x50}，条件属性C={a,b,c,d,e,f,g,h}。首先对连续属性值进行离散化处理，本文采用等频率区间法，制定划分区间个数为5，用对象总数除以区间个数得到每个区间的样本数，根据每个区间的样本数确定区间边界。对于定性属性本文采用5个评价等级来描述，如综合实力a={4，3，2，1，0}={重要，较重要，一般，较不重要，不重要}。将合作伙伴决策选择分为重要合作伙伴2、一般合作伙伴1及不作为合作伙伴0，所以决策属性为{p}={2，1，0}[6]。如表2所示：

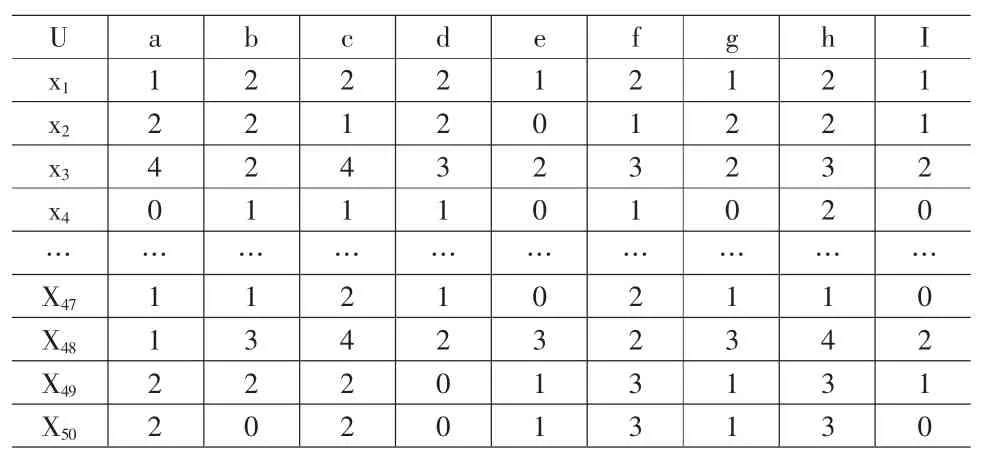
表2 联合风险投资候选合作伙伴统计决策表

计算其可分辨矩阵为：

由上述分辨矩阵可以得到其分辨函数F：

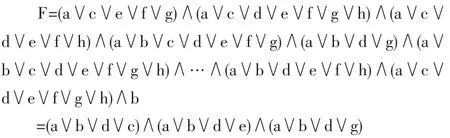
对分辨函数进行约简，得到{a,b,d,c}，{a,b,d,e}，{a,b,d,g}三个简式为条件属性C对决策属性{I}的约简集。约简集中没有属性f和h，由此可见，这里属性f（发展战略）与属性h（投资阶段）是决策的冗余属性，去掉属性f和h后并未改变决策系统的分类能力。经过约简最终得到财务状况、资源状况、互补性、声誉与信任、投资风格与综合实力六个指标。约简的结果与实践是一致的，因此，本文选择这六个指标对候选合作伙伴进行评价。

2 联合风险投资合作伙伴选择的BP神经网络模型

2.1 BP神经网络结构

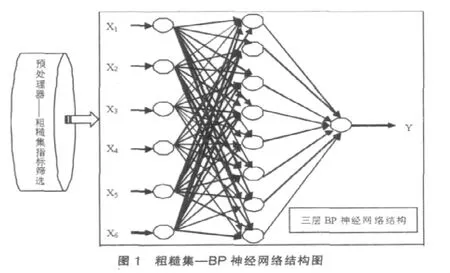
由于在理论上已经证明了具有三层结构（只有一个隐层）的BP网络能够逼近任何有理函数。因此，这里采用三层BP算法。输入层节点的个数与评价指标个数相对应，本文采用六个指标对联合风险投资候选合作伙伴进行评价，这样网络输入层的节点数为6。由于该网络输出结果只有一个指标即候选伙伴各指标的综合评价值，因此网络输出节点数为1。实验中隐含层的初选节点可按i=（输入层节点数+输出层节点数）1/2计算，考虑到单隐含层网络的非线性映射能力较弱，为了达到预定的映射关系，隐含层要多一点，因此最终确定隐含层节点个数为8。由此得到一个第一层含有6个输入神经元、隐含层含有8个神经元、输出层含有一个神经元的三层BP神经网络的结构，见图1所示。

以Inij和Oij分别表示第i层第j个神经元的输入与输出。

（1）第一层

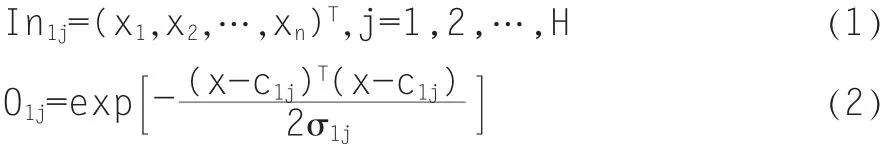
c1j和σ1j分别为聚类中心和方差，Oij为模式x属于聚类j的隶属度，即Oij=UFj(x)，H为聚类数。

（2）第二层

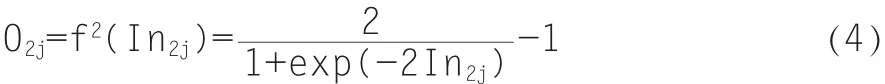
（3）第三层

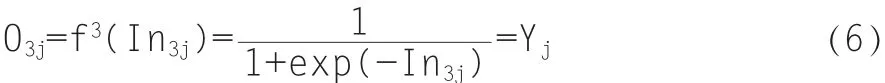
2.2 网络参数确定和模拟训练算法

神经网络中需要学习的权重参数主要是输出层的连接权重wij(i=1,2,…,m;j=1,2,…,n)，以及隐含层中隶属度函数的中心值cij和方差σij(i=1,2,…,m;j=1,2,…,n)。

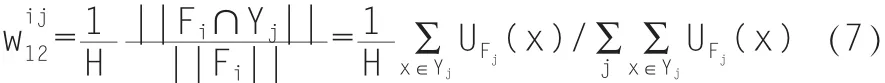
定义单个误差代价函数为[8]：

系统平均误差为：

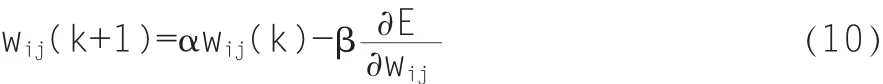
式中，α为动量因子，β为神经网络学习算法的学习率，0<β<1；wij(k+1)和wij(k)分别表示第k+1和第k次迭代时的权值。

由于输入数据在[0,1]之间，所以隐含层采用Tans ig转换函数，输出层采用Logsig转换函数，并且采用带有动量的梯度下降法训练网络。选取50个样本，循环训练网络100次，模型的实现过程利用Ma t l ab7.0语言编程实现。

训练网络的具体程序命令如下：

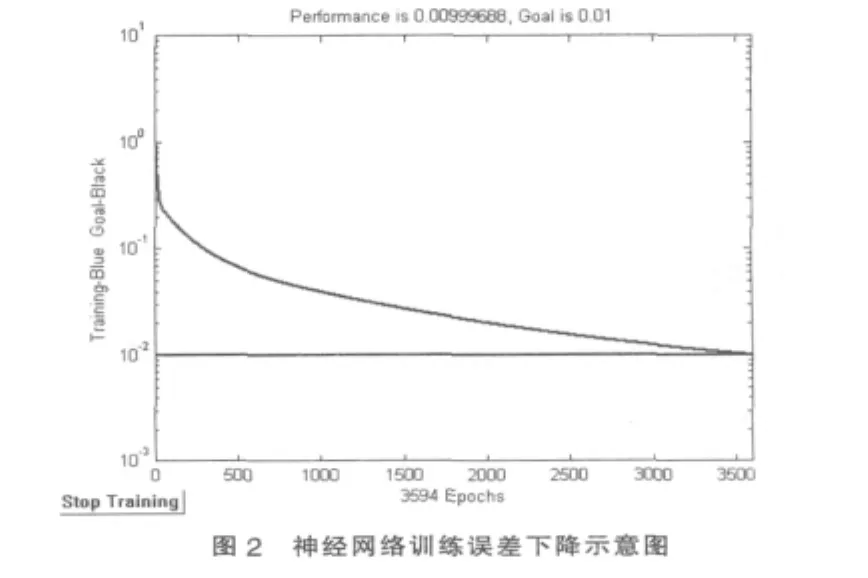
设定目标值为10-2，训练过程见如图2所示曲线，当训练3594步之后，系统显示“Performance goal met”，网络训练误差下降到目标值，网络停止训练。

2.3 基于粗糙集——神经网络模型的联合风险投资合作伙伴选择应用实例

设某主导型风险投资公司初步选定A，B，C和D四家候选风险投资公司，需要再从中选择出一家最优的合作伙伴。通过粗糙集指标的删选，最终选择合作伙伴现有的综合实力、资源状况、互补性、投资风格、公司声誉与信任、财务状况等六个重要评价指标。为了便于评价，应将各指标转换成具体的可测度的操作变量。这里，公司综合实力用公司竞争地位、公司规模和经营效率三个可测变量来反映；投资风格用投资领域、投资阶段和风险偏好三个可测变量来反映；资源状况用社会网络、人力资源状况和技术水平三个可测变量来反映；公司声誉与信任用商业信誉和历史业绩两个可测变量来反映；财务状况用公司注册资产、流动资产和投资能力三个可测变量来反映；互补性用互补性技巧和资源互补率两个可测变量来反映。

在这里就是要收集反映A，B，C和D四家风险投资公司综合实力、投资风格、资源状况、声誉与信任、财务状况、互补性六个评价指标的可操作变量的评价值，见表3所示。

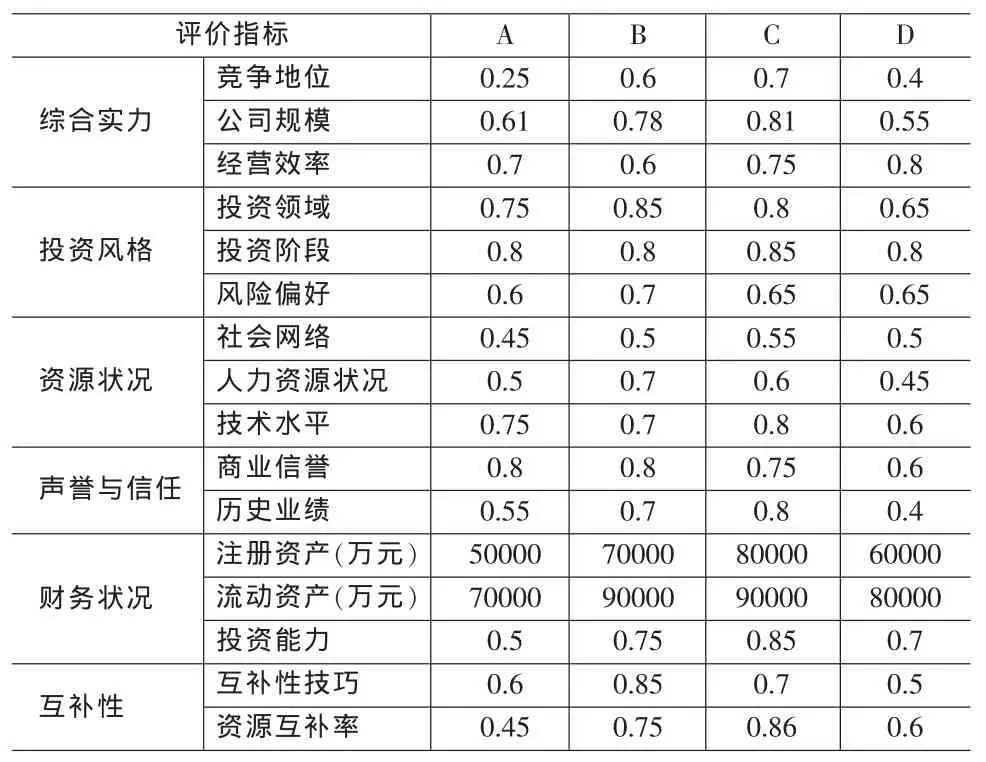
表3 四家风险投资公司评价指标数据表

首先计算A的评价值，将综合实力、投资风格、资源状况、声誉信任、财务状况和互补性归一化处理后作为BP神经网络的输入，即把0.6528，0.6883，0.6626，0.7133，0.6266和0.6314输入到训练好的神经网络，得到的输出结果为0.6233。同样可以得到B，C，D公司的综合评价值为0.6813，0.6911和0.6221，各公司详细数据见表4所示。

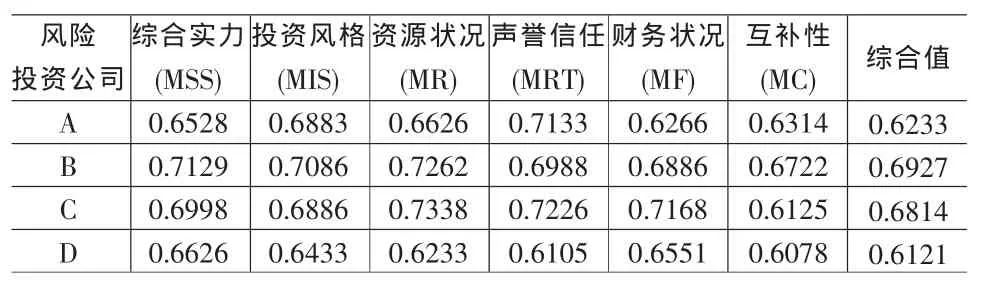
表4 四家风险投资公司综合评价数据表

可以看出公司C的综合值最大，其次为公司B，得出的初步结论是公司C为最优公司。为使结果准确可靠，可以将公司C和公司B的具体资料提交给有关专家进行最后的判断。

3 结束语

联合风险投资合作伙伴选择是个相对复杂的决策过程。本文分析了主导型风险投资公司选择联合风险投资合作伙伴的影响因素，使用粗糙集理论确定合作伙伴选择的评价指标，利用神经网络法建立合作伙伴选择模型，主导者可以通过衡量跟随者声誉、合作双方的互补性以及相容性的等方面的水平，做出最优的决策选择。将粗糙集理论与人工神经网络进行有机结合，可以有效弥补两种方法各自的缺陷，提高选择的速度与准确率。但需要注意的是，由于评价指标中存在许多难以量化的指标，给合作伙伴选择最优化决策带来了困难。同时，对神经网络模型来说，训练数据的合理性至关重要。不合理的数据会影响训练结果，影响网络参数的确定，进而必将影响应用效果。所以，探讨应用粗糙集理论确定训练数据集，剔除不合理的数据，增加合理的数据，不断调整——训练数据，可以达到较好的应用效果，这些问题都需要在后续的研究中做进一步深入地探讨。

[1]陈明，刘仲英.从动态联盟角度对联合风险投资的探讨[J].经济论坛，2005，(5).

[2]Ren Puli,Zheng Ouwang.Mining Classification Rules Using Rough Sets and Neural Networks[J].European Journal of Operational Research,2004,(157).

[3]吴金培，孙德山.现代数据分析[M].北京：机械工业出版社，2006.

[4]Johanna Pynna.Motivation for Syndication of Venture Capital Investments[Z].Tu-91.167 Seminar in Business Strategy and International Business,2004.

[5]卢燕，汤建影等.合作研发伙伴选择影响因素的实证研究[J].研究与发展管理,2006,18(1).

[6]周庆敏，殷晨波.虚拟企业伙伴选择的粗糙集方法[J].控制与决策，2005，(9).

[7]张东波.一种新型模糊-粗神经网络及其在元音识别中的应用[J].控制与决策，2006，21（2）.

[8]吴冲，吕静洁，潘启树，刘云涛.基于模糊神经网络的商业银行信用风险评估模型研究[J].系统工程理论与实践，2004，(11).

F830.5

A

1002-6487（2011）07-0183-04

教育部人文社科基金资助项目（10YJC630241）；江南大学引进人才项目

王雷(1979-)，男，安徽宿州人，博士，讲师，研究方向：创业投资与项目融资风险管理。

（责任编辑/浩天）