Black-Scholes期权定价的修正模型及其应用性研究
2011-11-01陈溟
陈溟
(内蒙古科技大学数理与生物工程学院,内蒙古包头014010)
Black-Scholes期权定价的修正模型及其应用性研究
陈溟
(内蒙古科技大学数理与生物工程学院,内蒙古包头014010)
文章在经典B-S模型的基础上引入了交易费用和连续支付的红利,对期权定价公式进行了进一步研究,并且给出了存在交易费用和连续红利时的期权定价公式。通过马钢权证和云化权证的实例分析,进一步说明有交易费用和连续红利存在对期权价格的影响,并对结果进行简要的分析。
B-S定价模型;交易费用;连续红利
1973年,美国芝加哥大学教授Black.F和斯坦福大学教授Scholes.M发表了一篇名为《The pricing of options and Corporate Liabilities》的著名论文,文章给出了Black-Scholes期权定价模型,推导出基于股票的任何一种衍生证券的价格应满足的微分方程,并成功地求解该方程,因此获得诺贝尔经济学奖。该理论及其以后的多种变形,对金融衍生工具市场的发展起了很大的推动作用。
经典的Black-Scholes模型在研究过程中没有考虑交易费用和连续红利,这使得该模型在现实金融市场中的实用性降低。为了提高该模型的实际应用性,使其更加符合现实的金融市场,本文在Black-Scholes模型假设的基础上,引入了交易费用和连续红利,并且给出了存在交易费用和连续红利情况下的期权定价公式,然后又引进两个具有代表性的权证,进一步研究分析,从而说明交易费用和连续红利的存在对期权价格的影响。
1 Black-Scholes期权定价模型及其修正模型
期权定价的Black-Scholes偏微分方程为:
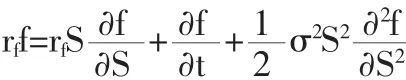
对应于可用标的变量S定义的所有衍生证券,此方程有许多解。解方程时得到的特定的衍生证券取决于使用的边界条件。对于欧式看涨期权,关键的边界条件为:
f=max(S-X,0)当t=T时
对于欧式看跌期权,关键的边界条件为:
f=max(X-S,0)当t=T时
求解该偏微分方程,可得欧式看涨期权定价公式为:
C(S,t)=SN(d1)-Xe-rf(T-t)N(d2)
看跌期权定价公式为:
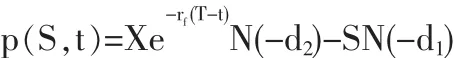
其中:
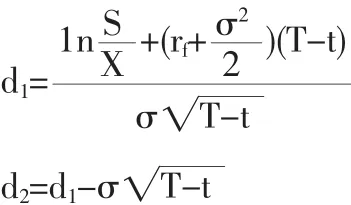
N(x)为均值为0标准差为1的标准正态分布变量的累计概率分布函数,f为期权价格,f=f(S,t),S为股票价格,X为执行价格,T为到期日,σ为股票回报的波动率,rf为瞬时无风险利率。
实际金融市场中,股票投资者经常会得到一定数量的红利,红利的支付有两种情形,每年在规定时间内支付或者按照一定比例连续支付,这里为方便只讨论连续支付的情形,在规定时间内支付可将除权除息日所支付的红利均摊到每一天,这样便可认为红利是连续支付的。现实交易中由于对投资组合的权重进行连续调整可引起交易成本不断增加,所以在修改模型时将交易成本考虑在内成为必然。Black-Scholes期权定价模型是在连续条件下,先在dt时间内对期权进行套期保值,再令dt→0而得到的,当考虑交易费用时,就不能无限次地对其进行套期保值,否则交易费用也会达到无穷,这是不可能的。因此,我们可适当修改该模型基本假设里的部分条件,对Black-Scholes方程基本假设做如下推广:
(1)股票价格过程遵循几何布朗运动,其离散形式为:

其中,准~N(0,1)其概率密度函数为:

这里△t不再是无穷小量,不再求趋于0的极限。
(2)期权在时刻t的价值遵循伊藤引理,其离散形式为:
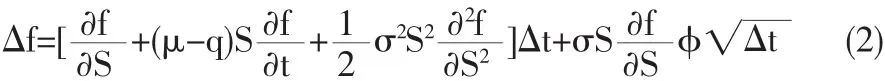
(3)股票连续支付红利,利率为q(t),无风险利率为r=r(t)。
(4)交易费用是投资者因买卖股票而产生的直接费用,一般由股票多头支付,并以交易额的固定比例M来表示。
构造投资组合π,买入一份期权合约f,卖出δ份股票S:
π=f-δS
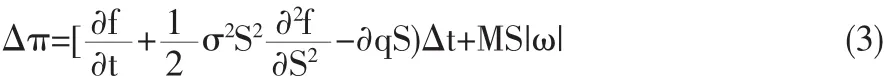
(3)式因套期保值策略而产生的交易份额ω为:
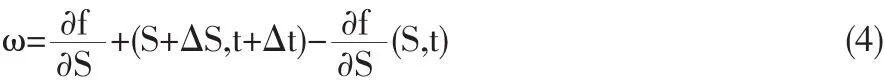
利用泰勒中值定理,将(4)式的第一项展开得:
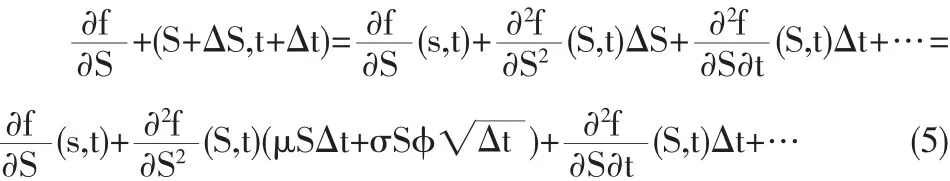
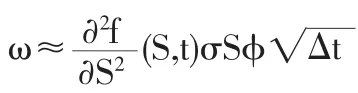
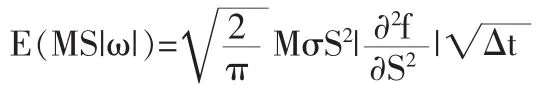
从而可得△π的数学期望为:

两边同时消去△t并移项,即可得到有交易成本和连续支付红利情况下欧式期权多头的定价方程为:

欧式期权空头的定价方程为:

2 求解修正后的Black-Scholes期权定价方程
用偏微分的知识来求解该方程比较繁琐,我们可以根据Black-Scholes模型的公式来推广有交易费用和连续支付红利的情况。将此股票与一只不支付红利的相似股票进行比较,红利的支付使得股票价格降低,所以支付连续红利率q使得股票价格的增长率比不支付时减少了q。

带入(6)式中,整理后,可得:

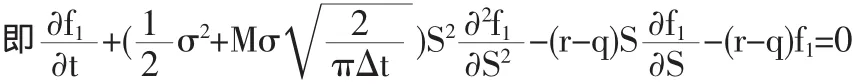

与B-S基本模型相比,我们可以看出有交易费用和红利的定价模型只差在无风险利率r上,只需r-q用代替r,便可得到有交易费用和红利的期权定价公式。
于是,有交易费用和红利的欧式看涨期权定价公式为:
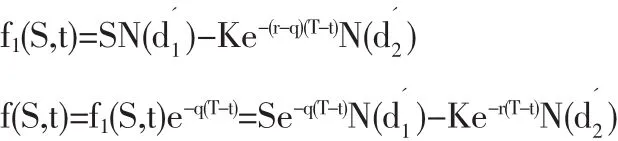
其中
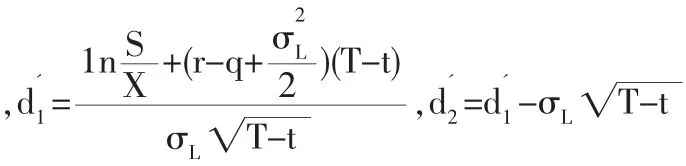
3 添加交易费和连续红利的期权定价公式的应用研究
我们选取两个具有代表性的权证—马钢权证和云化权证。马钢权证选择2006-11-29至2008-11-28时间段,云化权证选择2007-3-8至2009-3-7时间段(见表1),通过比较二者的B-S理论价格与修正价格的差异,进而说明交易费用和连续红利对期权价格的影响。
3.1 马钢权证和云化权证的理论价格
3.1.1 马钢权证的理论价格
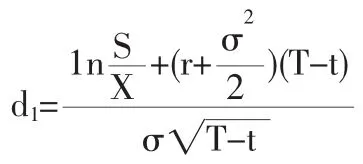
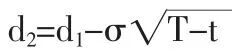
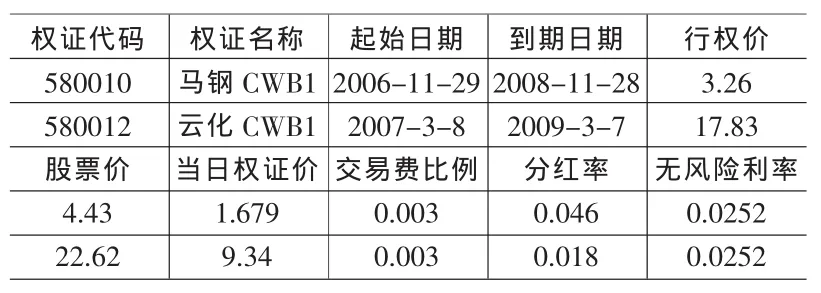
表1 马钢权证和云化权证的有关数据
由表1可得,S=4.43,X=3.26,T-t=2,r=0.0252,c=1.679,通过Matlab软件编程,可得马钢权证的隐含波动率σ为0.5136,d1=1.7096,d2=0.9832

表2 B-S理论价格与有交易费和连续红利的权证价格
查表有:N(d1)=0.956,N(d2)=0.836
则马钢权证的B-S理论价格为1.6437。
3.1.2 云化权证的理论价格
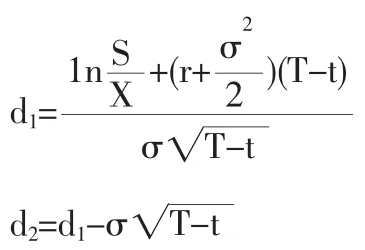
由表1可得,S=22.62,X=17.83,T-t=2,r=0.0252,c=9.34通过Matlab软件编程,可得云化权证的隐含波动率σ为0.6543,d1=1.5486,d2=0.6232
查表有:N(d1)=0.9384,N(d2)=0.7295
则云化权证的B-S理论价格为8.8589.
3.2 考虑有交易费和支付连续红利情况下的权证价格
3.2.1 马钢权证的修正价格
有交易费用和支付红利时的期权定价公式为:
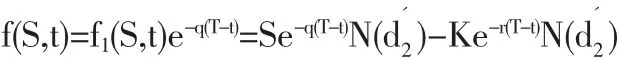
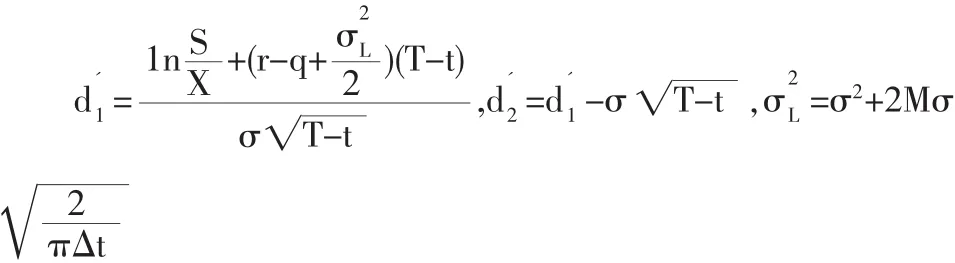
马钢权证相关数据:S=4.43,X=3.26,T-t=2,r=0.0252,q=0.046,M=0.003
又由上可得马钢权证的隐含波动率为0.5136,则可计算σL=0.517
那么可求得有交易费用和红利的马钢权证的修正价格为1.3836。
3.2.2 云化权证的修正价格有交易费用和红利时的期权定价公式为:

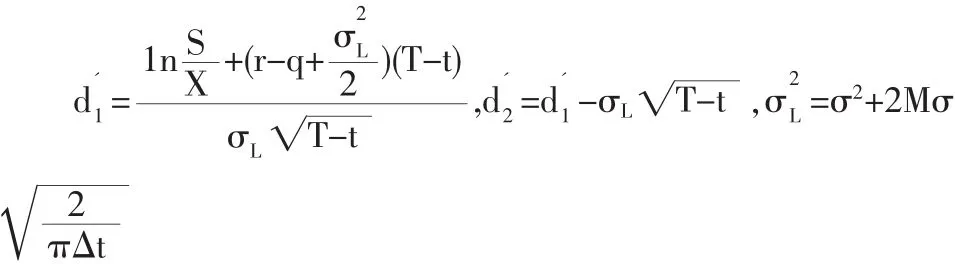
云化权证相关数据如下:
S=22.62,X=17.83,T-t=2,r=0.0252,q=0.018,M=0.003,σ=0.6543,σL=0.6577
则可得有交易费用和红利时的云化权证的修正价格为8.3104.
3.3 结果分析
马钢权证和云化权证的B-S理论价格与修正价格见表2与图1、图2。
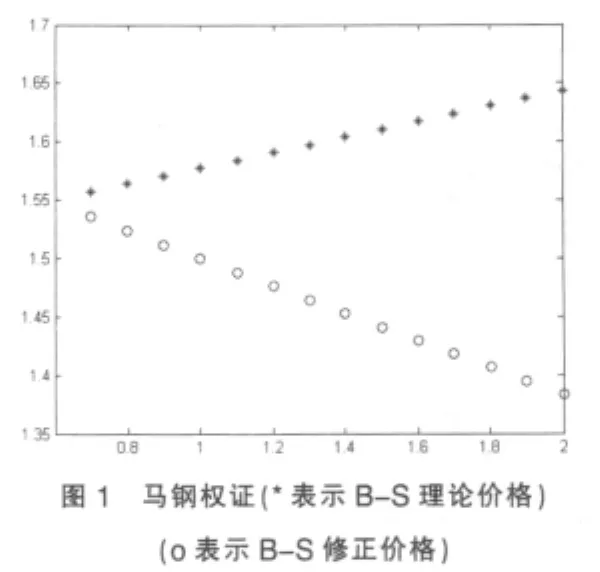

根据以上实证分析,我们将有交易费用和支付连续红利情况下的权证价格与经典的B-S定价模型的结果进行比较分析,结果如下:
(1)从散点图中我们可以看出,有交易费用和连续支付的红利存在时的权证价格比B-S理论价格偏低。
(2)对于马钢权证来说,考虑交易费用和支付连续红利情况下的权证价格比经典的B-S定价模型的权证价格降低了15.82%.
(3)对于云化权证来说,考虑交易费用和支付连续红利情况下的权证价格比经典的B-S定价模型的权证价格降低了6.19%。
目前,我国权证市场中,交易费用一般为千分之三,如果大客户和券商协议降佣,那么交易费用将更低,特别是在目前我国股市还没有做空机制的情况下,不能无限次地进行套期保值,所以就一次单边交易而言,交易费用通常可以忽略不计。
[1]约翰·赫尔,张陶伟译.期权、期货及其它衍生产品[M].北京:华夏出版社,1999.
[2]姜礼尚.期权定价的数学模型和方法[M].北京:高等教育出版社,2003.
[3]郑晓迎,陈金贤.有交易成本的期权定价研究[J].电子科技大学学报,2000.
[4]李春泉,刘新平.Black-Scholes模型期权定价方法及其应用[J].重庆工商大学学报:自然科学版,2006,23(4).
F201
A
1002-6487(2011)07-0135-03
陈溟(1972-),男,内蒙古包头人,硕士,副教授,研究方向:金融数学。
(责任编辑/亦民)
