模糊神经网络优化间谐波检测方法①

王旻鹤， 刘一江， 彭楚武

(1.湖南大学电气与信息工程学院， 长沙 410082；2.湖南大学土木工程学院， 长沙 410082)

模糊神经网络优化间谐波检测方法①

王旻鹤1， 刘一江2， 彭楚武1

(1.湖南大学电气与信息工程学院， 长沙 410082；2.湖南大学土木工程学院， 长沙 410082)

电力系统中电力电子元件大量应用可产生间谐波。它不但对用电设备产生影响，而且不易估计，给谐波治理带来了一定的困难。针对间谐波检测，先采集大量数据进行离线计算，利用一种改进的模糊神经网络得到满足误差要求优化模糊神经网络参数。在线计算利用这些参数，能够在短时间内得到满足误差要求的盖氏圆方法参数、ESPRIT算法的采样间隔和采样个数，使得信号源个数、间谐波频率和幅值能够准确判断。

间谐波； 旋转不变子空间算法； 盖氏圆方法； 模糊神经网络

电力电子元件的广泛应用，使得电力系统中产生谐波和间谐波。文献[1～3]中分别利用prony算法、Pisarenko算法和支持向量机算法进行间谐波检测，但其信号源估计与谐波检测算法均是分开的，对于不同信号重新计算自回归(autoregressio-

n)模型阶数[1，2]和选取盖氏园调整因子[3]都需要一定时间。在估计间谐波的过程中，采样个数及采样间隔也需要实验者通过经验或反复实验得到。本文利用一种改进的模糊神经网络，该网络经过学习后，可算出盖氏圆方法的参数以及ESPRIT算法所需的采样点个数和采样时间，不需要实验者再设定

采样参数值，从而得到准确频谱图。

1 一种改进的模糊神经网络

Araujo[4，5]提出了一种改进的模糊神经网络，该网络仅引入一个新的自由度就产生出完全不同的输入输出映射。

R∶ifx1isMi1and…andxmisMi1

thenyi=a0pi0+a1pi1x1+…+anpinxn

(1)

式中，R为第i条规则，xi为系统输入，pin为第i条规则下第n个神经网络权值，Mi1为系统模糊子集，αi为新引入的一个关系函数，它关于系统输入的函数，yi为第i条规则的输出。因此有

(2)

其中μi(x)为系统模糊子集Mi1的隶属函数，y为系统输出。

2 基于ESPRIT算法和模糊神经网络的间谐波检测方法

在电力系统中，间谐波模型表示为

(3)

(4)

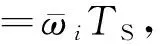
(5)

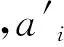
(6)

其中x(i)为第i时刻采样值。由(6)式可得

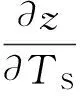
(7)

在ESPRIT算法[6～9]中，采样个数过少和采样间隔过大会影响准确性，个数过多和间隔过小会浪费系统资源。此外，由文献[10，11]可知，盖氏圆参数D(L)对信号源数的正确判断产生影响。因此有必要建立一个系统对盖氏圆方法和ESPRIT算法中参数进行控制，并且利用这些参数来求得满足一定要求的间谐波频率估计值及其对应幅度估计值。因此，建立如下模糊神经网络模型

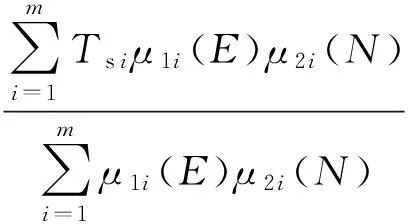
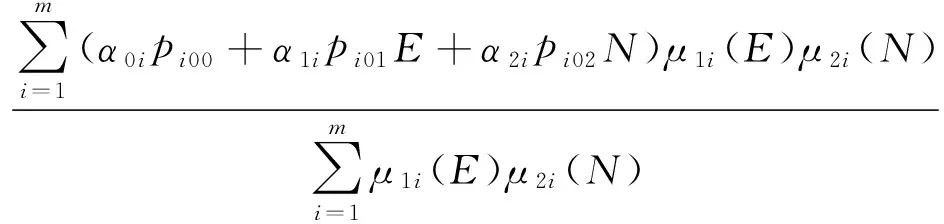
(8)

D(L)=

(9)

其中αji=c0ji+c1jiE+c2jiN，(i=1，2，…，M；j=0，1，2)

对于c0ji，c1ji，c2ji有

该控制系统是以误差和采样个数为输入，采样间隔与盖氏圆调整因子为输出的双输入双输出系统。它通过ESPRIT算法及式(8)计算得出的信号估计值求出目标函数误差，该误差和当前采样个数经过模糊化，利用最速下降法调节神经网络各参数，输出即采样间隔值和盖氏圆调整因子将会被下一时刻ESPRIT算法及盖氏圆方法所使用。选取误差小，采样个数较小且采样间隔较大的一组估计值。由(9)式可得

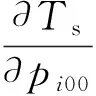
(10)

由式(7)，(10)可得

(11)

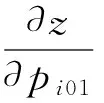
理想状态下对于采样数据的协方差矩阵元素值可由下式得到

(12)

其中x*(n+m)为x(n+m)的共轭转置。对于采样个数较多时可得

(13)

其中i=0，1，…，k，k为协方差矩阵的维数。

离线和在线计算中，为了避免采样个数过大造成大运算量，采样个数大于100时，令(13)式中N为100，采样个数不足100时，则采用当前时刻计算得出采样个数。式(12)中采样数据利用个数为N-1+m，而式(13)采样数据利用个数为N-1+m+k，较式(12)能够更全面反映采样数据情况。

各信号值存在误差相抵，为确保频率和幅值估计值的准确性，引入方差作为判断依据。设采样函数方差为σ1，估计值方差σ2，噪声方差为σ3，因此有σ2≤σ2+σ3，又因为σ2>10σ2，可采用式(14)作为判断标准。

|σ1-σ2|<ε

(14)

3 仿真分析

电力系统信号可能包含直流、谐波、间谐波、基波和噪声。仿真中采用的模型如式(15)所示。

x(k)=1+0.5cos(2π×22Tsk)+

0.3cos(2π×23Tsk)+0.3cos(2π×

50Tsk)+n(k)

(15)

其中n(k)为σ2为0.05的零均值平稳高斯白噪声，Ts为采样间隔。

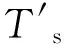
在线计算中，选取ε=0.01且z<10-6。采用本文方法计算50次可得结果见图1～图5。

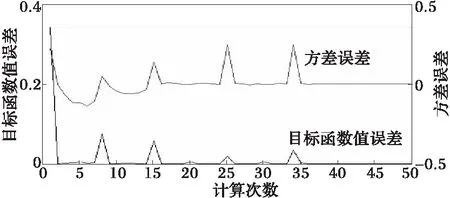
图1 目标函数误差及方差误差Fig.1 Error of object function and variance

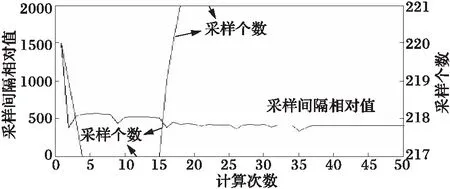
图2 采样间隔相对值及采样个数Fig.2 Sample number and the relativevalue of sample interval

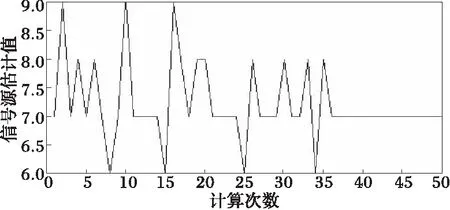
图3 信号源估计个数Fig.3 Estimation of source number

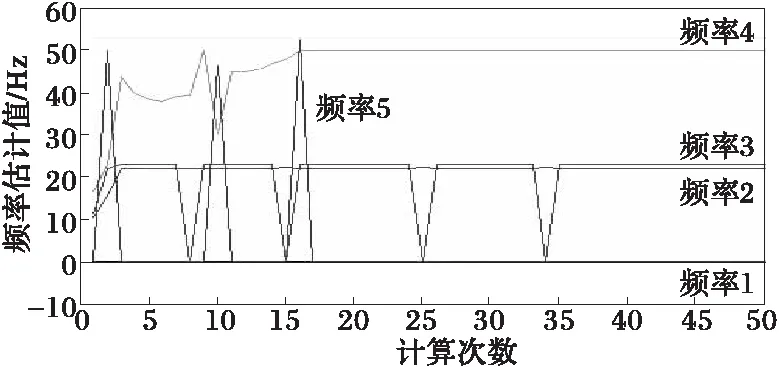
图4 频率估计Fig.4 Frequency estimation

图1表明运算中目标函数误差、方差误差迅速减小，且最终稳定在一定值。采样个数变化不大。当第32次运算时频率和对应幅值达到设定要求，如表1所示。采样中，采样频率必须在原频率2倍以上。电力系统基波周期为0.02 s，图2采样个数为

图5 幅值估计Fig.5 Amplitude value estimation表1 满足设定要求时各参数值Tab.1 All parameter value when objects meet

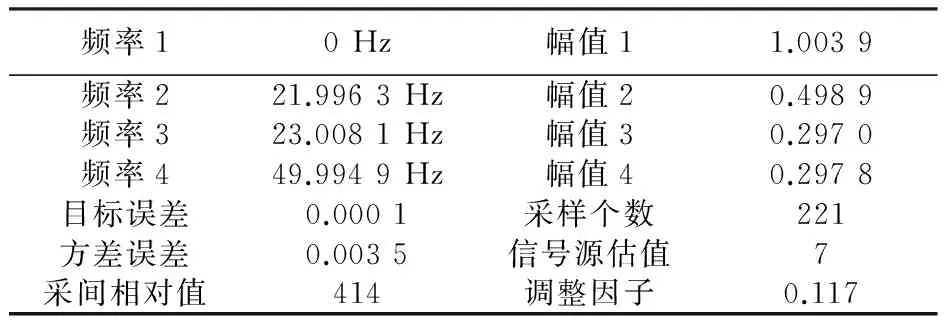
频率10Hz幅值11.0039频率221.9963Hz幅值20.4989频率323.0081Hz幅值30.2970频率449.9949Hz幅值40.2978目标误差0.0001采样个数221方差误差0.0035信号源估值7采间相对值414调整因子0.117

220左右，而式(13)中个数选为100。因此采样间隔应不大于0.005 s，即其相对值应不大于500。由图2和表1可知，采样间隔相对值由初始1 500，最终稳定在400左右，满足采样定理。式(4)和式(12)可知信号源个数为7，由图3可知，采样个数估计在35次计算后稳定在7。图4、图5所示，计算过程中信号源个数估计不同产生频谱泄漏和栅栏效应，但随着信号源个数准确估计，这些现象也随之消失。离线计算后，由式(2)可得到图6～图7。

由图6可知，当误差在0左右且采样个数在500以内时，输出值能保证满足采样定理。表1中，该网络输出值在400左右，该值能在实际应用中提高CPU利用率，将其节约的资源用于其它功能实现。目标函数误差较大时，输出值不满足采样定理，这与实际相符合。对于传统模糊神经网络，其映射是一个线性曲面，图8中，其参数与改进模糊神经网络相同情况下，映射值均大于改进网络，即使能得到满足采样定理的值，也由于线性曲面的单调性使采样间隔值不满足采样定理或者浪费CPU资源。仿真中，采样间隔初始值设为0.015，需将其控制到0.005以内，不确定因子α使得模糊神经网络无需通过调整权值就能减小目标函数误差。图8中，目标函数误差为0且采样个数小于500时，两种网络映射值之差超过0.02，即用传统网络得到的采样间隔，间谐波不能正确估计。同样对于盖氏圆参数D(L)，两个网络在模糊化部分相同，因此二者映射图形状大致相同。由图7可知，误差较大或者采样个数较大时，输出值均不在有效范围内，这与实际情况相符。图9中，采样点数较小且误差较大时，传统值小于改进值，其值虽可能满足采样定理，但其目标函数误差较大，模糊神经网络会继续计算，目标函数误差得到较小值时，其输出值反而得不到满足要求的输出值。另外，步长选取也十分重要，误差会因为步长较大，使输出值产生在不同区域，前后变化可能会很大，造成发散，不利于系统控制。因此，合理选择步长变得十分重要。

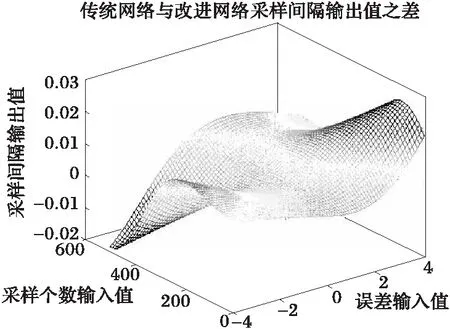
图6 改进模糊神经网络式(15)映射图Fig.6 15th equation's mapping

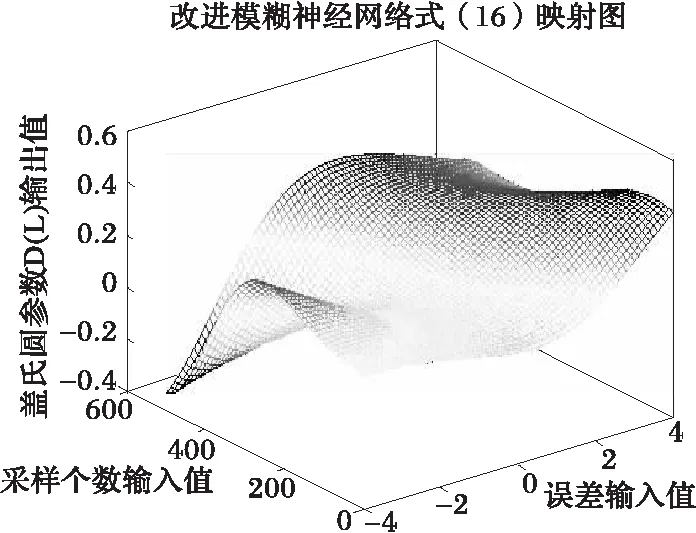
图7 改进模糊神经网络式(16)映射图Fig.7 16th equation's mapping

在传统模式下，再利用式(5)所得到结果分别与改进后结果相减得到图9和图10。

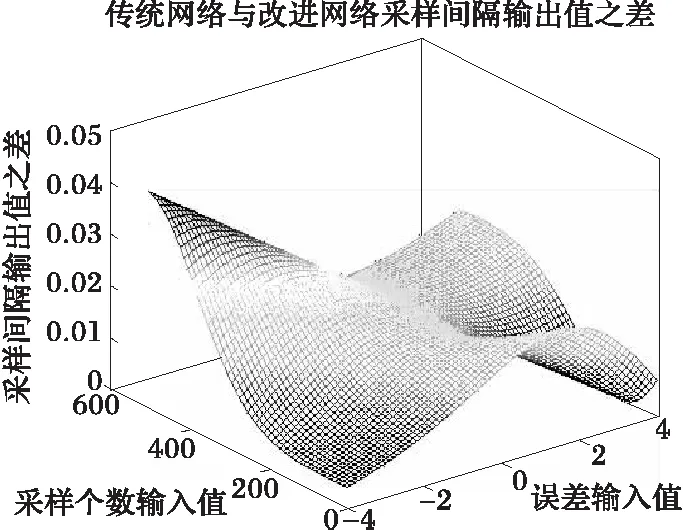
图8 传统与改进模糊神经网络采样间隔映射之差Fig.8 Sample interval's difference between the classicand the improved T-S fuzzy model

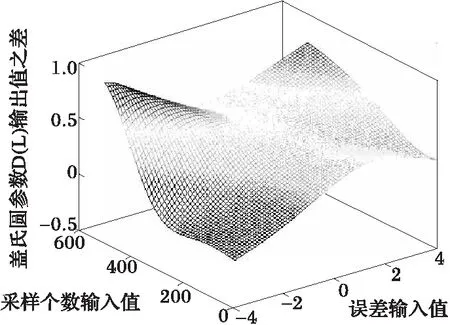
图9 传统与改进模糊神经网络盖氏圆参数映射差Fig.9 D(L)'s difference between the classic T-Sand the improved fuzzy model

4 结语

ESPRIT算法利用数据协方差矩阵信号子空间的旋转不变性，它计算量较小，实时性优于MUSIC等算法。本文中介绍模糊神经网络较传统网络不需改变权值就能达到减小误差。利用改进网络计算得到盖氏圆参数、采样间隔和采样个数，信号源个数能够准确估计，原信号频率和幅值能够在一定误差内得到估计。仿真中，在线计算时间大约50 s左右，实时性上还有改进的地方，计算中会出现各信号正负误差相抵消，方差判断的引入虽能提高估计值准确性，但不能消除各信号误差正负相抵现象。另外，如何在不同区域有效选择步长将是以后工作的目标。

[1] 郝江涛，刘念，幸晋渝 (Hao Jiangtao, Liu Nian, Xing Jinyu).电力系统间谐波分析(Study on interharmonic of power system)[J].电力自动化设备(Electric Power Automation Equipment)，2004，24(12):36-39.

[2] 乐叶青,徐政(Le Yeqing，Xu Zheng). 电力系统间谐波及其检测方法综合分析(The analysis of interharmonic and its detecting methods)[J].电气应用(Electrotechnical Application), 2006，25(12):110-113.

[3] 高培生，谷湘文，吴为麟(Gao Peisheng, Gu Xiangwen, Wu Weilin). 基于空间谱和支持向量回归机的间谐波分析(Interharmonic analysis based on spatial spectrum and support vector regression machine)[J].电力系统自动化(Automation of Electric Power System)，2007，31(24):67-70.

[4] Araujo Ernesto. Improved Takagi-Sugeno fuzzy approach[C]∥IEEE International Conference on Fuzzy Systems, HongKong, China: 2008.

[5] Takagi Tomohiro, Sugeno Michio. Fuzzy identification of systems and its applications to modeling and control[J].IEEE Trans on Systems, Man and Cybernetics,1985,15(1): 116-132.

[6] Roy R, Paulraj A, Kailath T. ESPRIT-a subspace rotation approach to estimation of parameters of cissoids in noise[J].IEEE Trans on Acoustics, Speech and Signal Processing, 1986, 34(5):1340-1342.

[7] Roy R， Paulraj A, Kailath T. Estimation of signal parameters via rotational invariance techniques-ESPRIT[C]∥IEEE Military Communications Conference， Monterey, USA:1986.

[8] Roy R, Paulraj A, Kailath T. Comparative performance of ESPRIT and MUSIC for direction-of-arrival estimation[C]∥Asilomar Conference on Circuits, Systems and Computers, Pacific Grove, USA: 1987.

[9] Roy Richard, Kailath Thomas. ESPRIT-estimation of signal parameters via rotational invariance techniques[J].IEEE Trans on Acoustics, Speech and Signal Processing, 1989,37(7): 984-995.

[10]Wu Hsien-Tsai, Yang Jar-Ferr, Chen Fwu-Kuen. Source number estimators using Gerschgorin disks[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing, Adelaide, Australia: 1994.

[11]Wu H T, Yang J F, Chen F K.Source number estimation using transformed Gerschgorin radii[J].IEEE Trans on Signal Processing, 1995,43(6):1325-1333.

[12]李正军，杨洪军，宋晓庆(Li Zhengjun, Yang Hongjun, Song Xiaoqing). 新型电力网络仪表的谐波测量方法与实现(Harmonic measuring approach and realization using new type electric meter)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2006，18(3) :28-33.

[13]王永良，陈辉，彭应宁,等.空间谱估计理论与算法[M].北京:清华大学出版社，2005.

彭楚武(1949-)，男，教授，主要从事嵌入式系统应用，计算机集成制造系统。Email:cwpeng@hnu.cn

OptimizedInterharmonicsEstimationUsingTagaki-SugenoFuzzyModel

WANG Min-he1， LIU Yi-jiang2， PENG Chu-wu1

(1.College of Electrical and Information engineering, Hunan University,Changsha 410082, China；2.College of Civil Engineering, Hunan University, Changsha 410082, China)

The wide application of electronic and electrical elements in power system can bring out the interharmonics. They not only influence the equipments, but also are hard to be estimated correctly. So it is difficult to control the interharmonics. In this paper, a huge number of samples are firstly calculated off line by using an improved T-S Fuzzy Model introduced by this paper to obtain the optimized T-S model parameters. Then the Gershgorin Disks parameter, sample interval and sample number can be obtained in a short time of online calculation by using optimized T-S Model. At last, the sources number, interharmonics frequency and amplitude could be estimated correctly.

interharmonic； ESPRIT algorithm； Gershgorin Disks； Tagaki-Sugeno fuzzy model

TP391.9

A

1003-8930(2011)03-0118-05

2009-11-09

2009-12-15

王旻鹤(1985-)，男，硕士研究生，主要从事电力系统自动化及自动控制方面研究。Email:wangminhe@yahoo.com.cn

刘一江(1955-)，男，教授级高工，主要从事电力系统自动化，自控控制，人工智能方面研究。Email:j_liu1@126.com