RELAX算法在间谐波检测中的应用①

季 宇， 孙云莲， 李 晶

(1.武汉大学电气工程学院， 武汉 430072； 2.五环化工有限公司， 武汉 430072)

RELAX算法在间谐波检测中的应用①

季 宇1， 孙云莲1， 李 晶2

(1.武汉大学电气工程学院， 武汉 430072； 2.五环化工有限公司， 武汉 430072)

间谐波是频率非基波整数倍的谐波成分，传统谐波测量方法将会因为非同步采样而产生泄漏误差。为准确测量间谐波，文中提出基于松弛谱估计(RELAX)的检测方法。因为该方法针对复信号进行分析，在检测前需先对采样信号进行希尔伯特变换构成复序列，计算结束后的相位测量结果也要进行修正。由于RELAX算法的复杂度集中在快速傅里叶变换(FFT)处，故相比于其它方法其计算速度是有优势的。最后通过对具体间谐波信号的仿真测量，验证了该方法的有效性和实用性。

间谐波； 非同步采样； RELAX算法； 希尔伯特变换； 快速傅里叶变换

随着电力系统中非线性负荷的大量投用，电力系统中的谐波情况也愈发复杂，不仅存在频率是基频整数次的整数次谐波，而且存在非整数次谐波成份。这些对电力系统的安全、稳定运行造成了极大的危害。而对谐波间谐波进行有效分析治理的基础便是对其准确的检测。

目前电力系统中的间谐波源主要是以电弧炉为主的波动性负荷及变频调速装置类的非线性负荷。此外，高压直流输电技术从原理上分析等同于交直交的变流系统，因此也可划为第二类间谐波源。从频域上分析，前者由于电弧阻抗的时变性导致频谱呈连续谱，后者则是具有特征频率的离散谱，且其频率可通过互调理论进行分析。无论是连续谱还是离散谱都具有间谐波的统一特征即频率非工频整数倍且幅值较小，这一特征决定了以往很多谐波检测方法对于间谐波将不再适用。目前间谐波的检测方法可以分为两大类，即非参数估计法和参数估计方法。前者包括快速傅里叶变换(FFT)、插值傅里叶变换[1～3]、小波分析[4]、支持向量机法[5]等；后者则主要是基于现代谱估计的方法[6]，包括奇异值最小二乘法、PRONY法、BURG法以及一大类空间谱估计方法。这些方法中快速傅里叶变换作为最常用的方法在非同步采样时会出现谱峰偏离，引起参数估计误差。插值傅里叶方法针对传统傅里叶变换进行算法修正，通过加窗和插值的方法克服频谱泄露及栏栅效应。然而，这类算法运算量较大，一般需要求解高阶方程。小波分析类方法是将观测信号利用子带分离技术进行频带划分，得到各个频率谐波。而小波滤波器的混叠性及噪声敏感是这类方法的缺点。支持向量机法是利用支持向量机的回归特性，结合迭代变权方法估计谐波参数。这种方法能够保证全局收敛性，且估计参数是全局最优的，但参数选择问题限制了该方法的广泛应用。参数估计方法中奇异值最小二乘法和PRONY法可以直接测量间谐波的全部参数，但计算量较大，且由于在推导公式中存在假设条件(如白噪声假设)，因此实际检测结果可能存在较大偏差。BURG法实质是格型滤波算法，利用莱文森递推公式计算模型参数。该方法避免了求解相关矩阵，但对于高阶模型及大样本情况分析效果较差。子空间法通过分离信号与噪声空间给出观测信号的伪谱，因此只能用于频率检测，且在信噪比较低时效果较差。本文中介绍的RELAX方法属于非参数估计法，能够准确计算谐波的全部参数。同时，计算过程中利用了FFT，但克服了FFT非同步采样时的估计误差，且具有一定抗噪性能。

1 RELAX算法介绍[8，9]

RELAX算法是一种具有超分辨率的谱分析算法，该算法假设复谐波模型[3]为

n=0，1，…，N-1

(1)

其中αk是谐波幅值，此处可理解为带相位信息，即αk=|αk|ejφ，en是观测噪声，K是谐波个数(实际运算中可以先使用熵值估计方法或FFT方法对主要谐波个数进行估计)。在此基础上将谐波参数估计问题转化为下面的优化问题：

J1(f1，α1，…，fk，αk)=

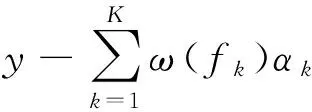
(2)

其中y=[y0y1…yN-1]T，ω(fk)=[1，ej2πfk，…，ej2πfk(N-1)]T，‖·‖2表示欧氏范数。设

P=[ω(f1)，ω(f2)，…，ω(fk)]

(3)

因为P的列向量相互独立，故可将范式中的表达式理解为一个向量投影问题，则原优化式可表示成

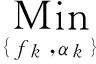
(4)

由泛函分析可知，当投影向量作正交投影时可取得最小范数解，最小范数解(即最小二乘解)为

(5)

此时待估计的参数只有各个谐波频率。设谐波频率矢量f=[f1，f2，…，fk]T，及正交投影矩阵Ω=P(PHP)-1PH，优化式最小范数值即为正交投影矩阵补空间上投影长度。基于此，优化目标简化为：

J2(f1，f2，…，fk)=‖Ω⊥y‖2=

‖(I-Ω)y‖2

(6)

上面分析的过程将多参数估计转化为单一的频率参数的估计，然而计算最小范数解相对复杂，但可以基于此得到一个很重要的结论，就是当谐波个数K小于实际个数时， 已测出的部分谐波参数仍是可靠的，这是由正交理论决定的。

J3(fk)=Min‖yk-αkω(fk)‖2

(7)

求解该优化式，可得

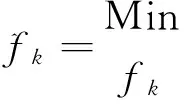
Maxfk|ωH(fk)yk|

(8)

(9)

由此可以看出，fk的估计可以利用FFT方法进行计算，且幅值最大处的频率，即为所估计频率值，而该频率处FFT变换幅值与估计幅值成比例。实际应用RELAX方法计算时，在计算出某一对参数后，应利用优化式J1判断参数估计是否合适，如果未达到误差要求则循环迭代，直到参数估计的足够好后再计算后面的参数。这样每增加一对参数的估计，就需对前面已估计出的参数进行更新。

需要说明的是上面介绍的RELAX算法不能直接用来分析实信号，但通过以下步骤修正后可以准确检测谐波(间谐波)信号参数。

步骤1X(t)=x(t)+jH[x(t)]

在这样反差显著且形式紧迫的大环境下， 结合计算机信息和3D图形处理分析技术以及互联网技术的发展契机，BIM应运而生, 并迅速引起行业内领袖企业的关注和重视。 BIM作为一个完整的概念被明确提出可以回溯到20世纪90年代 [4]。而其真正兴起是在新千年后，在软件行业巨头Autodesk， Bentley Systems和Graphisoft等公司的共同推动下，一系列以数字化建造为核心概念的新一代软件产品(例如AECOsim以及稍后占北美市场主导地位的Autodesk Revit)被推出，以取代传统CAD产品作为行业变革的技术基础并支持建筑行业内数字信息交互和协同合作。

(10)

步骤2φ=φ+π/2

(11)

(注：H[·]表示Hilbert变换，且Hilbert变换在负频处有π/2的相位延迟)

至此，整个算法流程如下：

(1)估计主谐波个数K。

(2)初始化αk及fk，对观测数据进行HILBERT变换，取变换后复值观测数据作待测数据。

(3)计算待估计分量yk。

(5)根据优化目标J1判断参数估计是否准确，满足条件则依次估计其它分量参数否则重复估计已测参数。

(6)对估计相位进行修正。

2 仿真实验

构造如下含间谐波的虚拟电压信号，

V(t)=10sin(2π50t+π/4)+

2sin(2π73t+π/3)+

4sin(2π77t+π/5)+

6sin(2π121t+π/6)+e(t)

(12)

其中加入了信噪比为30dB的高斯白噪声。下图分别是观测信号波形及使用FFT对观测信号进行频域分析结果(频域图中幅值已归一化)。

为使用RELAX方法，需先确定K值。现定义谱峰分离判别式

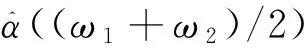
(13)

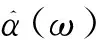
当两个频率处的谱峰满足上述关系，即可认为被正确识别。本例中经计算K为3，这是由于73 Hz与77Hz频率接近而无法分辨。为测试算法容错能力，实验中分别取K为3、4、5、6，测试算法的。图3表示RELAX算法在不同K值下的分析结果，表1是具体的误差分析。

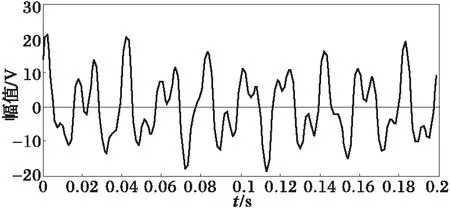
图1 混噪待测信号Fig.1 Signal mixed with noise

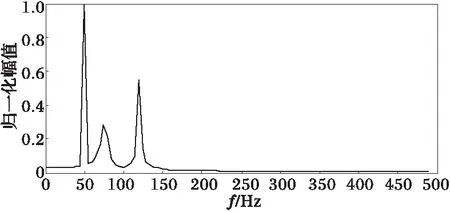
图2 FFT频域分析Fig.2 Frequency analysis via FFT表1 不同K值下RELAX算法误差分析Tab.1 Error analysis of RELAX algorithm in different case of K

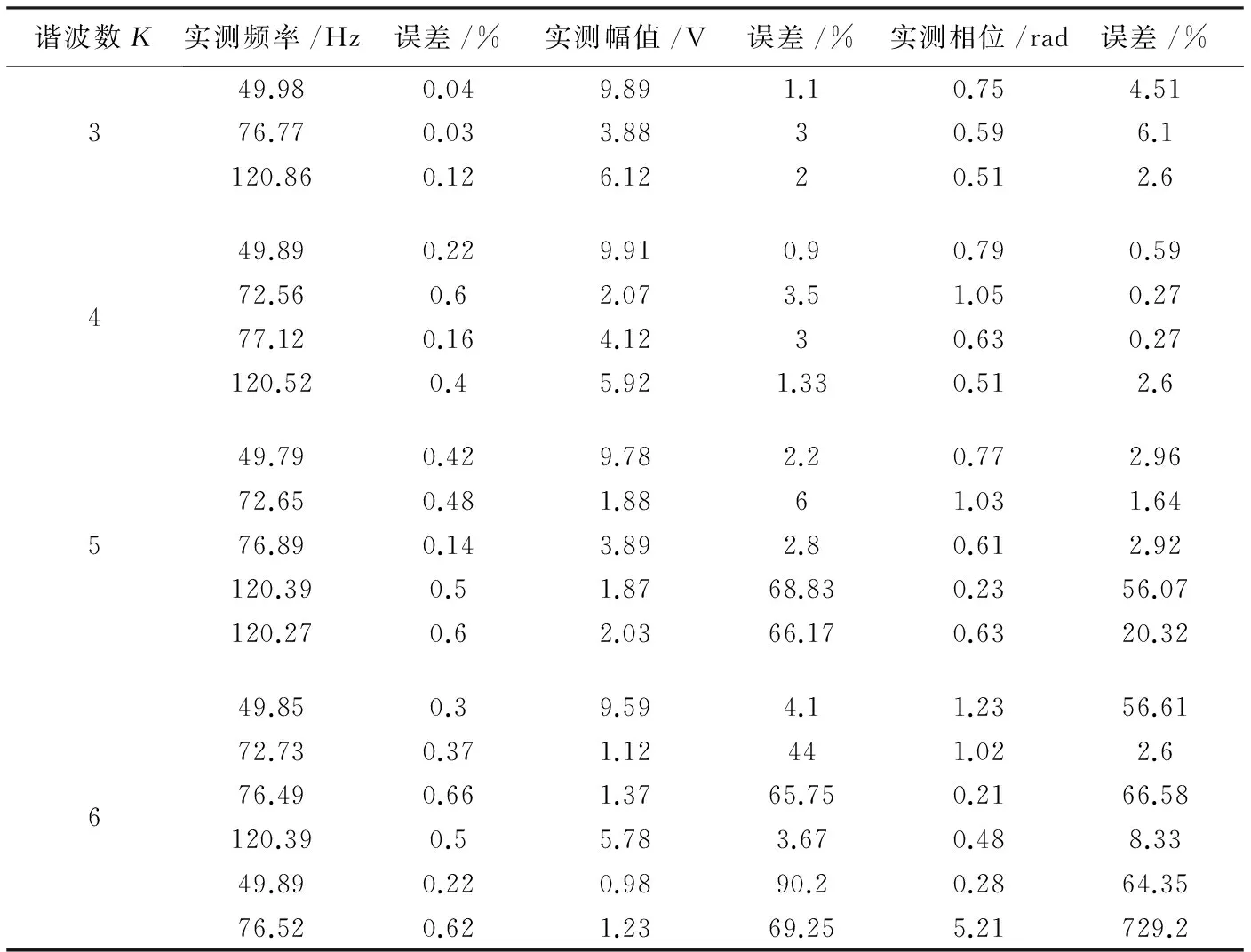
谐波数K实测频率/Hz误差/%实测幅值/V误差/%实测相位/rad误差/%349.980.049.891.10.754.5176.770.033.8830.596.1120.860.126.1220.512.6449.890.229.910.90.790.5972.560.62.073.51.050.2777.120.164.1230.630.27120.520.45.921.330.512.6549.790.429.782.20.772.9672.650.481.8861.031.6476.890.143.892.80.612.92120.390.51.8768.830.2356.07120.270.62.0366.170.6320.32649.850.39.594.11.2356.6172.730.371.12441.022.676.490.661.3765.750.2166.58120.390.55.783.670.488.3349.890.220.9890.20.2864.3576.520.621.2369.255.21729.2

结合图3和表1可以看出，当谐波估计数K小于实际谐波个数时，RELAX算法仍可准确检测谐波参数。当K大于实际个数时，会产生某些频率谐波的重复测量，并导致这些频率处谐波参数估计不准确。因此只需要将这些频率谐波合并，并相应减少K值重复计算便可将参数准确测量。

图3 RELAX在不同K值下频率估计Fig.3 Frequency estimation via RELAX by different K

3 结语

RELAX算法的计算主要使用FFT，因此在实时性上得到保障，经实际测试虽然计算精度不如PRONY及SVD-TLS方法，但测量时间远小于二者。与传统FFT方法相比较，该方法不存在频谱泄露问题，可准确计算频率接近的谐波参数，因此可以应用于间谐波的实时测量分析中。

[1] 王波, 杨洪耕(Wang Bo, Yang Honggeng).基于AR谱估计和插值FFT的间谐波检测方法(A method for Interharmonic measurement based on AR model spectral estimation and interpolation FFT algorithm)[J].继电器(Relay), 2006, 34(4):49-52,56.

[2] 张伏生, 耿中行, 葛耀中(Zhang Fusheng,Geng Zhongxing,Ge Yaozhong).电力系统谐波分析的高精度FFT算法(FFT algorithm with high accuracy for harmonic analysis in power system)[J].中国电机工程学报(Proceedings of the CSEE), 1999 ,19(3):63-66.

[3] 易立强, 邝继顺(Yi Liqiang, Kuang Jishun). 一种基于FFT的实时谐波分析算法(FFT-based algorithm for real-time harmonic analysis)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2007, 19(2):98-102.

[4] 薛惠, 杨仁刚(Xue Hui, Yang Rengang).利用Morlet连续小波变换实现非整次谐波的检测(Morlet wavelet based detection of noninteger harmonics)[J].电网技术(Power System Technology), 2002, 26(12):41-44.

[5] 占勇, 丁屹峰(Zhan Yong, Ding Yifeng). 电力系统谐波分析的稳健支持向量机方法研究(A robust support vector algorithm for harmonics analysis of electric power system)[J].中国电机工程学报(Proceedings of the CSEE), 2004, 24(12):43-47.

[6] 石敏, 吴正国, 伊为民(Shi Min, Wu Zhengguo, Yi Weimin). 基于多信号分类法和普罗尼法的间谐波参数估计(Inter-harmonic parameter estimation based on multi-signal classification and Prony method)[J].电网技术(Power System Technology), 2005, 29(15):81-84.

[7] Ling J, Stoica P, Li J，etal.On using cyclic algorithms for sinusoidal parameter estimation[J].Electronics Letters, 2008, 44(19):1160-1161.

[8] Li Jian , Stoica Petre. Efficient mixed-spectrum estimation with applications to target feature extraction[J].IEEE Trans on Signal Processing, 1996, 44(2):281-295.

[9] IEC 61000-4-30,Testing and measurement techniques-Power quality measurements methods[S].

ApplicationofRELAXAlgorithmonInterharmonicDetection

JI Yu1， SUN Yun-lian1， LI Jing2

(1.School of Electrical Engineering, Wuhan University, Wuhan 430072, China；2.Wuhuan Chemical Co.,Ltd., Wuhan 430072, China)

Interharmonic is the special harmonic element which is not an integer multiple of the fundamental. Due to the asynchronous sampling problem, serious leakage error may arise with the measurement method for normal harmonics. In this paper, a new approach for sinusoidal parameter estimation based on RELAX(Relaxation algorithm)is presented. To get the correct result, the proposed method depends on two additional steps: the Hilbert Transform of the samples and the phase revise. The method can make the faster measurement in comparison with others since the Fast Fourier Transform(FFT) takes up the main calculation time of the RELAX. Finally, the simulation results have verified the effectiveness and practicability of the algorithm.

interharmonic； asynchronous sampling； relaxation algorithm； Hilbert transform； fast Fourier transform

2009-11-09

2010-01-18

TM93

A

1003-8930(2011)03-0135-04

季 宇(1982-)，男，博士，研究方向为电能质量分析与控制。Email:jiyu820507@gmail.com

孙云莲(1962-)，女，博士生导师，研究方向为电能质量分析与控制，分布式发电并网控制技术。Email:ylsun@whu.edu.cn

李 晶(1980-)，女，硕士，研究方向为化工设计中的配电技术。Email:lijingdk@cwcec.com