水平管加压密相煤粉气力输送沙丘流的数值模拟

蒲文灏, 赵长遂

(1.南京航空航天大学 能源与动力学院,南京210016;2.东南大学 能源与环境学院,南京210096)

密相气力输送是一种低速气体颗粒输送技术,具有低能耗、低磨损、大输送量的特点,因而在化工、冶金及能源等众多工业中得到了广泛应用.煤粉加压密相气力输送已成为气流床加压气化的关键技术[1].例如,在我国引进的国际先进煤粉加压气化技术——Shell气化技术中,就是利用惰性气体氮气将煤粉连续地在高固气比条件下输送到加压(3.0～4.0 MPa)气化炉中进行煤气化反应,而在其合成气中的氮气含量仅占4%.由于目前试验手段和试验条件的限制,有关加压密相气力输送的试验研究主要集中在压损分析、流动相图及信号分析等方面[2],有关固相速度和浓度分布的试验数据尚未见报道.对高压密相水平管气力输送过程进行了数值模拟,可为研究水平管内流动特性与流动形态的关系提供参考.

Tsuji等[3]首先用硬球模型对水平管内栓塞流进行了模拟研究.该方法需要对所有颗粒运动进行跟踪,但由于受到计算能力的限制,目前还不能用于处理工程中大量的颗粒数目.Levy[4]应用双流体模型模拟了水平管内颗粒栓塞的流动,得到了栓塞运动过程中流场参数的变化规律.由于Levy的模型采用了经验本构关系,因而不适用于其他密相输送工况.顾正萌和郭烈锦[5]应用颗粒动理学双流体模型模拟了水平管内颗粒栓塞的流动,得到了栓塞运动过程中流场参数的变化规律,但是他们的模型中没有考虑颗粒之间的摩擦应力.

颗粒沙丘流是水平加压密相气力输送系统中的典型流型之一.在水平管底部,颗粒间长时间接触并相互挤压,此时颗粒间的摩擦应力是颗粒相应力的主要部分.在管道顶部,颗粒浓度较低,固相应力主要是由颗粒碰撞和平移引起的,此时颗粒动理学应力占主导.在沙丘流的界面处,两者的贡献都不可忽略.因此,只有将摩擦应力和动理学应力综合考虑才能正确地描述颗粒在水平管内的流动状态.

Johnson和Jackson[6]首先提出了一个经验的摩擦正应力模型.在此基础上,Johnson等[7]和Ocone等[8]针对不同的玻璃珠颗粒分别给出了其各自的摩擦应力模型.Lu等[9]比较了不同模型对喷动流化床模拟结果的影响,认为摩擦应力的模型和参数对密相气固流动有重要影响.Srivastava等[10]提出了摩擦-颗粒相动理学应力封闭模型,并将其运用到上升管和垂直料斗的二维模拟中.假设模型在高颗粒浓度气固两相流动中,由于颗粒间相互接触产生的颗粒摩擦应力和由于颗粒间碰撞产生的动理学应力同时存在.动理学应力由颗粒动理学方法确定,而对摩擦应力,需要考虑速度应变率和颗粒缓慢松弛到屈服表面的变化.Makkawi和Ocone[11]采用Tardos等提出的固相应力表达式,结合颗粒动理学模拟研究了水平渠道内气固流动的行为.

针对加压密相气力输送,本文对Johnson等[7]提出的摩擦正应力模型和Syamlal等提出的摩擦剪切黏度模型进行了修正,并将其与颗粒动理学理论相结合,建立了可以描述加压密相气力输送的气固湍流流动工况的三维多相流模型.在模型中,同时考虑了颗粒间碰撞和摩擦力作用,还考虑了气相和颗粒团湍流脉动之间的相互作用.采用该模型对加压密相条件下水平管内煤粉沙丘流进行了三维数值模拟并将模拟结果与测量得到的压降梯度、电容层析成像(ECT)测量的横截面颗粒浓度分布和拍摄得到的沙丘流流动形态进行了比较.

1 试验装置

图1为高压超浓相煤粉气力输送系统示意图.高压氮气经过缓冲罐分成流化风、充压风和补充风三路,发料罐内的煤粉经流化风驱动进入输送管道,在发料罐出口引入补充风调节输送管道内的固气比,充压风用于维持发料罐内的压力稳定.收料罐中的含粉气流经布袋除尘器分离煤粉后放空,收料罐内的压力由电动调节阀根据设定值自动调节.

图1 高压超浓相煤粉气力输送系统示意图Fig.1 Schematic of the pressurized super dense phase pneumatic conveying system

输送管路由16 mm×3 mm的不锈钢直管和弯管组成,输送距离为53 m.在管道的不同部位装有4个差压传感器,分别用于测量水平管、垂直管、水平弯管和垂直弯管测试段的差压,同时在输送管道上安装了一个高频压力传感器,并在输送管道沿途布置了ECT测量系统和可视化拍摄系统,分别用于测量管道横截面颗粒浓度分布和拍摄管内流型.在一个高压料罐上安装了3个高精度箔式电子秤,用于实时测量煤粉料罐内的煤粉质量.试验中的压力、流量、差压及煤粉质量的测量数据均采用计算机数据采集系统采集.在试验中,采用的煤粉粒径为37 μm,密度为1 350 kg/m3,高压氮气来自南京某气体厂,其纯度为99.9%.

2 数学模型

2.1 控制方程

连续方程

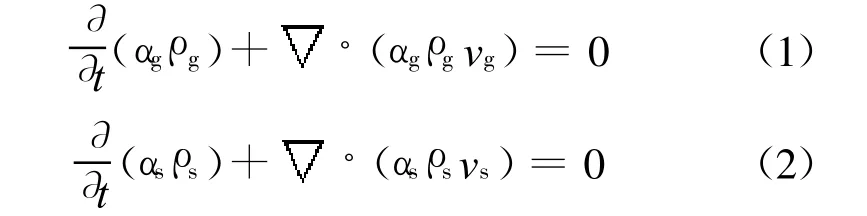
动量方程

式中:αg、αs分别为气、固相体积分数;ρg、ρs分别为气、固相密度;vg、vs分别为气、固相速度;τg、τs分别为气、固相应力张量;β为气、固相间的动量变换系数,kg/(m3·s).

气固相之间的作用力很复杂,在水平管密相输送中曳力是相间作用力的主导因素,因此在颗粒高浓度气固两相流动模拟中只考虑了曳力的作用.到目前为止,还没有严格的气固相间作用力模型,大多数研究均采用经验或半经验模型来预测气固相间的作用力.当 αg≤0.8时,曳力系数 β采用Ergun在1952年提出的公式;而当αg＞0.8时,曳力系数β则采用Wen和Yu在1966年提出的公式,上述具体公式参见文献[12].

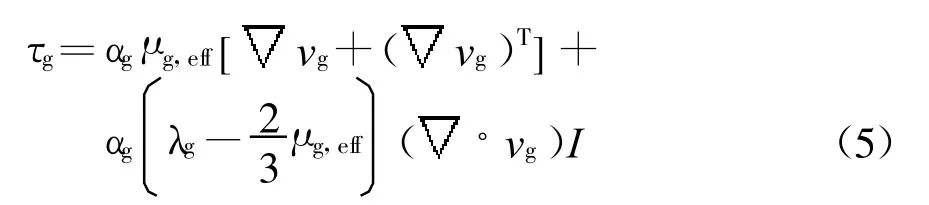
Savage[13]认为:颗粒的相应力可以看成是动理学应力和摩擦应力的简单和,各自单独作用.

式中:τks为颗粒动理学应力张量;τfs为摩擦应力张量.

考虑了颗粒碰撞和平移作用,采用Gidaspow[13]提出的公式进行闭合.

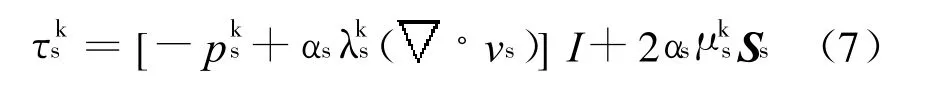
式中:Ss为固相速度变形率张量.

Johnson等[6]的摩擦正应力模型认为:当颗粒浓度大于0.5时,颗粒间才存在摩擦应力.实际上,当颗粒浓度小于0.5时,颗粒间也存在摩擦力.在水平沙丘流中,颗粒浓度在0.1～0.5变化的区域是颗粒从快速流动区域向缓慢剪切区域过渡的中间区域,也是上、下层间动量和质量交换剧烈的区域,对颗粒流动的影响很大,直接影响流型的变化.当颗粒浓度在0.1～0.5变化时,摩擦应力的作用逐渐增强,且不可忽略.笔者认为:当颗粒浓度大于0.1时,必须考虑颗粒间的摩擦应力;当颗粒浓度小于0.1时,可以忽略颗粒间的摩擦应力.通过模拟的煤粉颗粒的特性变化以及根据模拟的压降损失与试验测量值的对比,将摩擦应力模型中的经验参数F修改为0.1,摩擦应力的公式为[10]:

式中:F、r、s均为经验常数,F=0.1,r=2,s=5;αmsin=0.1;n表征屈服面处于膨胀还是压缩状态;pf为摩擦应力张量的法向应力;pc为临界状态压力;ds为颗粒粒径,m;φ为颗粒内摩擦角,(°).

颗粒相的拟温度方程

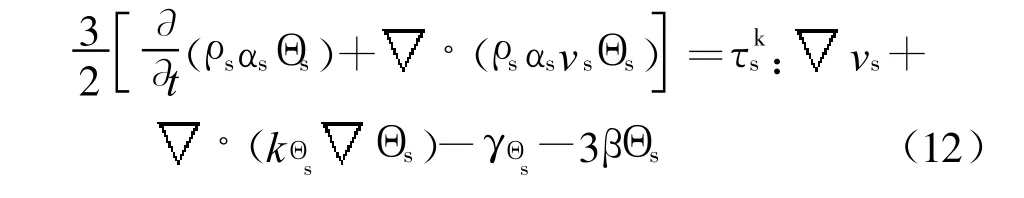
式中:Θs为颗粒伪温度为颗粒的脉动速度;kΘs为固相扩散系数,kg/(m·s);γΘs为固相非弹性碰撞耗散率,kg/(m·s3).

湍流输运方程

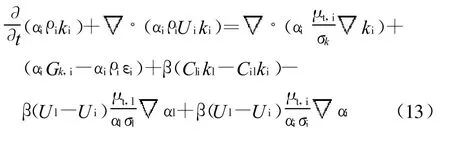
式中:U为相平均速度;Gk为湍动能产生项,kg/(m·s3);ε为湍流耗散率,m2/s3;k为湍动能;下标i为气相时,下标l为固相;下标i为固相时,下标l则为气相.

2.2 模拟条件

本文对内径为10 mm,长为5 m的水平管进行了数值模拟.气相轴向入口速度采用光滑管充分发展湍流分布,固相轴向入口速度采用均匀分布,入口固相浓度按已知的颗粒质量流率和固气比确定,气相轴向出口采用压力出口条件.初始时刻,管道内各相速度和固相体积浓度设为零.颗粒在壁面的剪切力采用Srivastava等[10]提出的滑移条件.

3 结果与讨论

3.1 预测压降梯度与试验结果的对比

图2 压降梯度随表观气速的变化Fig.2 Pressure drop gradient vs.superficial velocity

图2 为压降梯度随表观气速的变化.从图2可知:当煤粉质量流率Ms分别为0.177 kg/s和0.167 kg/s时,在相同的固相输送量下,随着表观气速的增加,压降梯度下降,当气速增加到某一值时,压降梯度达到最小值,此时的速度为最佳经济输送气速;当表观气速继续增加时,压降梯度呈现上升趋势.由于在水平输送管中,表观气速较低时,管道底部煤粉沉积层较厚,因此颗粒与壁面的摩擦阻力是输送阻力的主要部分.随表观气速的增加,颗粒与壁面的摩擦阻力快速减小,在低气速下,气速增加引起的阻力损失增加较小,因此总输送阻力减小.而当表观气速较高时,颗粒的沉积厚度较薄,随着表观气速的增加,颗粒与壁面的摩擦阻力减小,但气体与壁面的摩擦阻力快速增加,与气体速度的2～3次方成正比,造成输送阻力增加.因此,随着表观气速的增加,压降梯度呈现先减少后增加的趋势.

3.2 预测颗粒浓度分布与ECT测量结果的比较

杨道业[14]将ECT技术应用于高压浓相煤粉气力输送,得到了流动过程中管道横截面上的颗粒浓度分布.为了验证模拟结果的可信度,笔者对杨道业的试验工况进行了模拟,并将模拟结果与测量结果进行了比较.表1为加压密相煤粉气力输送参数.

表1 加压密相煤粉的气力输送参数Tab.1 Parameters of pressurized dense phasepneumatic conveying of pulverized coal

图3为预测和ECT测量得到的煤粉颗粒浓度分布.从图3可以发现:预测得到的煤粉颗粒浓度分布与ECT测量的结果相吻合,煤粉颗粒沉积在管道底部并呈现月牙形.根据图3(a)中颗粒的浓度分布,将截面分为3个区域:悬浮区域a、过渡区域b和沉积区域c.沉积区域位于管道底部,区域内煤粉颗粒浓度较高,颗粒之间保持长时间的接触;悬浮区域位于管道上部空间,煤粉颗粒浓度较低,在此区域内,颗粒以悬浮状态运动;位于两者之间的是过渡区域.一般认为:过渡区域内的煤粉颗粒与悬浮区域和沉积区域内的煤粉颗粒间的动量和质量交换非常剧烈.悬浮区域内的一些煤粉颗粒由于重力的作用,进入到过渡区,同时也有一些过渡区域的煤粉颗粒由于碰撞或气流的携带,从过渡区进入悬浮区.从图3中可以看出:各个区域之间并没有明显的边界,表明在密相输送中,煤粉颗粒在管道内的运动非常复杂,受到多种因素的影响.

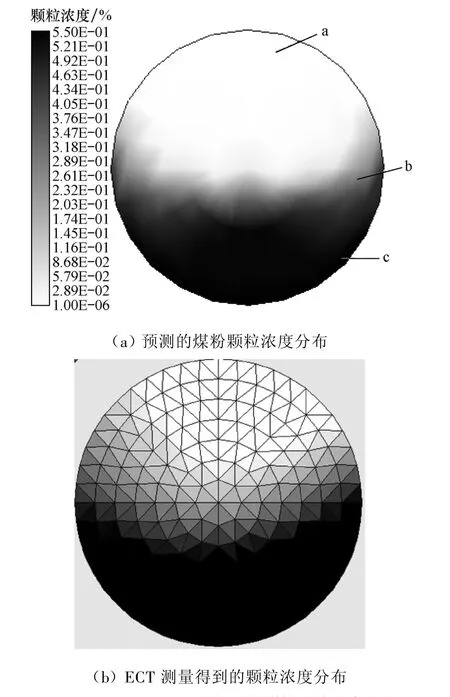
图3 预测和ECT测量得到的煤粉颗粒浓度分布Fig.3 Distribution of pulverized coal concentration predicted and measured by ECT

3.3 加压密相煤粉沙丘的流动模拟

3.3.1 单个沙丘的形成与运动过程

为了模拟高压密相水平管中单个煤粉沙丘流动的特点,对质量流率为0.167 kg/s、表观气速为4.26 m/s、粒径为37μm、煤粉体积浓度为0.292 8的试验工况进行了数值模拟.煤粉沙丘的形成通过控制颗粒相的入口条件实现.图4为进口处煤粉颗粒相浓度随时间变化的曲线.当t＜0.3 s时,入口处煤粉颗粒浓度保持恒定值,在此时刻后,入口煤粉颗粒浓度为零.

在此条件下,笔者模拟得到了煤粉单个沙丘形成和运动的瞬态过程.图5为煤粉单个沙丘的运动过程.从图5可看到:流动方向为从右向左流动;沙丘头部坡度陡峭,沙丘尾部坡度较平缓,这与Jaworski和Dyakowski[15]的试验结果相吻合.当煤粉沙丘移动后,有少量煤粉颗粒停留在管道底部,形成一个很薄的沉积层.随后,这些煤粉颗粒逐渐被气流带走,最终管道内不再有煤粉颗粒停留.

图4 进口处煤粉颗粒浓度随时间的变化Fig.4 Pulverized coal concentration at inlet vs.time

图5 煤粉单个沙丘的运动过程Fig.5 Motion process of single dune of pulverized coal

图6为管长Z=2 500 mm处单个煤粉沙丘压力随时间变化的曲线.从图6可看到:当煤粉沙丘未到时,压力没有变化.当煤粉沙丘头刚到达时,由于沙丘作用,压力开始升高;当煤粉沙丘尾部离开后,压力上升到一个稳定状态.当煤粉沙丘头部到达管道出口,压力开始缓慢下降,随着煤粉沙丘逐渐流出,压力逐渐恢复到原来的数值.模拟得到的压力随时间变化的曲线与范椿[16]描述的单个料栓输送时压力随时间变化的规律一致.

3.3.2 煤粉沙丘流的形成与运动过程

为了模拟高压密相水平管中煤粉沙丘流的流动,对质量流率为0.167 kg/s、表观气速为4.26 m/s、粒径为37μm、煤粉体积浓度为0.292 8的试验工况进行了数值模拟,煤粉沙丘的形成通过控制颗粒相的入口条件实现.图7为入口处煤粉颗粒相浓度随时间变化的曲线.在图7中可看到:每隔0.1 s,入口处的煤粉固相体积浓度波动一次,每次增加或减少的量是稳定给料的50%.

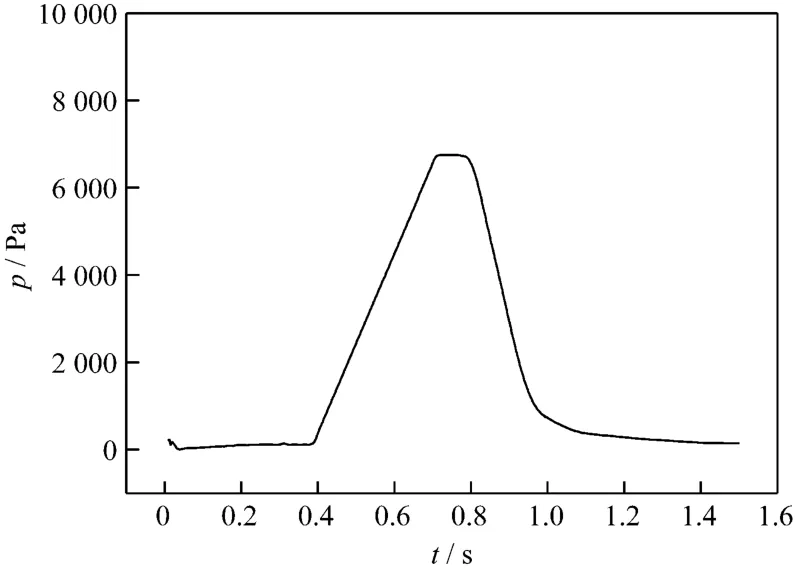
图6 Z=2 500 mm处单个煤粉沙丘压力随时间的变化Fig.6 Pressure of single dune of pulverized coal vs.time at Z=2 500 mm

图7 入口处煤粉颗粒相浓度随时间变化的曲线Fig.7 Pulverized coal concentration at inlet vs.time

图8为模拟的煤粉连续沙丘流的运动过程.在图8中,煤粉颗粒自右向左运动,并呈现周期性波的形状向前移动.

图8 模拟的煤粉连续沙丘流的运动过程Fig.8 Simulated motion process of continuous dune of pulverized coal

4 预测结果与拍摄结果的比较

图9是煤粉粒径为300μm时拍摄的水平管内煤粉流动状况的照片,其中流动方向自右向左,图9中的煤粉沙丘连续向前运动的情况与图8中的模拟结果相似.

图9(b)是单个沙丘逐渐流过管道的情况,图9(b)中最下面的照片是煤粉沙丘流过后,煤粉停留在管道内的情况,与图5中t=1.1 s的模拟结果相似.将拍摄结果与图5和图8的模拟结果进行比较后可以看出:模拟的煤粉沙丘形状和运动过程都与拍摄的图片很相似,模拟结果再现了煤粉沙丘流的形成与运动过程,在一定程度上反映了沙丘流动的特征,表明本文采用的固相应力模型能够正确描述高浓度煤粉颗粒在水平管内的流动工况.表2为高压浓相煤粉的气力输送参数.

图9 拍摄的煤粉连续沙丘流和单个沙丘流Fig.9 Pictures of continuous dune flow and single dune flow of pulverized coal

表2 高压浓相煤粉的气力输送参数Tab.2 Parameters of pressurized dense phasepneumatic conveying of pulverized coal

5 结 论

(1)随着表观气速的增加,颗粒浓度减小,压降梯度呈现先减小后增大的趋势.

(2)在横截面上,颗粒分布呈现上窄下宽趋势,且颗粒在管道底部沉积并呈现月牙形状.

(3)模拟预测了单个沙丘和连续沙丘的形成与运动工况.

(4)将颗粒静摩擦力与颗粒动理学理论相结合的数学模型对处理气力输送气固两相流,特别是高压、高浓度密相气力输送具有很好的适应性,模拟结果与试验结果吻合较好,可以成为高压密相气力输送系统设计和优化的工具.

[1] 王辅臣.大规模高效气流床煤气化技术基础研究进展[J].中国基础科学,2008,10(3):4-13. WANG Fuchen.Progress on the large-scale and high-efficiency entrained flow coal gasification technology[J].China Basic Science,2008,10(3):4-13.

[2] 周云,陈晓平,梁财,等.不同平均粒径煤粉的高压密相气力输送[J].动力工程,2009,29(3):218-222. ZHOU Yun,CHEN Xiaoping,LIANG Cai,et al.Dense-phase pneumatic conveying for pulverized coal with different mean particle size under high pressure[J].Journal of Power Engineering,2009,29(3):218-222.

[3] TSUJI Y,TANAKA T,ISHIDA T.Lagrangian numerical simulation of plug flow of cohesionless particles in a horizontal pipe[J].Powder Technology,1992,71(3):239-250.

[4] LEVY A.Two-fluid approach for plug flow simulations in horizontal pneumatic conveying[J].Powder Technology,2000,112(3):263-273.

[5] 顾正萌,郭烈锦.水平管内栓塞流气力输送的动理学模拟[J].工程热物理学报,2006,27(1):75-78. GU Zhengmeng,GUO Liejin.Kinetic simulation of horizontal slug-flow pneumatic conveying[J].Journal of Engineering Thermophysics,2006,27(1):75-78.

[6] JOHNSON PC,JACKSON R.Frictional-collisional constitutive relations for granular materials,with application to plane shearing[J].J Fluid Mech,1987,176(9):67-93.

[7] JOHNSON P C,NOTT P,JACKSON R.Frictional collisional equations of motion for particulate flows and their application to chutes[J].J Fluid Mech,1990,210:501-535.

[8] OCONE R,SUNDARESAN S,JACKSON R.Gasparticle flow in a duct of arbitrary inclination with particle-particle interactions[J].AIChE,1993,39(8):1261-1271.

[9] LU Huilin,HE Yurong,LIU Wentie,et al.Computer simulation of gas-solid flow in spouted beds using kinetic-frictional stress model of granular flow[J].Chemical Engineering Science,2004,59(4):865-878.

[10] SRIVASTAVA A,SUNDA RESAN S.Analysis of a frictional-kinetic model for gas-particle flow[J].Powder Technology,2003,129(1/2/3):72-85.

[11] MAKKAWI Y,OCONE R.A model for gas-solid flow in a horizontal duct with a smooth merge of rapid-intermediate-dense flows[J].Chemical Engineering Science,2006,61(13):4271-4281.

[12] GIDASPOW D.Multiphase flow and fluidization:continuum and kinetic theory descriptions[M].New York,US:Academic Press,1994:316-325.

[13] SAVAGE SB.Analysis of slow high-concentration flows of granular materials[J].J Fluid Mech,1998,377:1-26.

[14] 杨道业.厚管壁气固两相流电容层析成像技术研究[D].南京:东南大学能源与环境学院,2008.

[15] JAWORSKI A J,DYAKOWSKI T.Investigations of flow instabilities within the dense pneumatic conveying system[J].Powder Technology,2002,125(2/3):279-291.

[16] 范椿.拴状流密相气力输送[J].力学进展,2002,32(4):599-612. FAN Chun.Plug flow dense phase pneumatic conveying[J].Advances in Mechanics,2002,32(4):599-612.