二维串列双圆柱层流对流传热的数值分析

胡瑞荣, 葛培琪, 闫 柯, 宿艳彩

(山东大学 机械工程学院,高效洁净机械制造教育部重点实验室,济南250061)

多圆柱绕流在海洋平台、输运缆线束、化学反应 塔及热交换管流动[1]等工程领域中应用非常广泛.多圆柱绕流时,由于圆柱间的相互作用,圆柱的压力分布、升阻力的大小及涡脱落现象与单圆柱绕流有着很大的区别.

在对流传热方面,国内外多位科研人员对单圆柱绕流传热进行过研究.Wushung FU等[2]对流体横掠单圆管的流场结构与对流传热特征进行了数值模拟,得出锁定现象对圆柱表面的对流传热有很大影响;Yongho LEE等[3]用试验方法研究了流体诱导振动单圆柱的传热特性,得出振动可以提高临界热流密度;俞接成等[4]通过数值模拟研究了空气低速绕流振动圆柱的对流传热特性,得出了振动频率和振幅影响强化传热效果的结论.但对于双圆柱绕流问题,不仅要考虑振动方式对传热的影响,还要考虑两圆柱的排列间距对传热的影响.目前,有关双圆柱绕流的研究主要集中在间距对圆柱升阻力特性及尾涡结构影响的研究,较少考虑间距对传热性能的影响.M.M.Zdravkovich[5]在对均匀来流中不同排列方式下双圆柱绕流问题的研究中发现:双圆柱绕流时升阻力特性及涡脱落现象与单圆柱绕流不同;郑廷辉等[6]采用有限体积法对串列双圆柱尾迹流进行数值分析,得出了间距比和旋涡脱落频率的关系.

笔者从强化传热考虑,采用流场分析软件Fluent对不同排列间距下二维双圆柱的传热特性进行了仿真分析,并结合振动强化传热,对不同排列间距比下的双圆柱沿流向振动时的传热性能进行了数值计算,为换热器管束排列间距的确定提供依据.

1 物理模型与计算参数

图1为流体横掠双圆柱的物理模型.图中x为横坐标,y为纵坐标,将串列放置的二维双圆柱的上游圆柱用c1表示,下游圆柱用c2表示,c1和c2的中心距为L,两圆柱直径均为D.

水流的来流速度恒定,水流温度为300 K,设两圆柱为等壁温条件,其温度均为350 K.

图1 流体横掠双圆柱的物理模型Fig.1 Phy sical model of flow transversely passing through the twin cylinders

当c1、c2静止和c1、c2沿流向振动时,间距比L/D均取为2.0～6.0,间距比变化步长为0.5;流向振动时,两圆柱均以正弦函数形式沿流向运动,其运动规律为:

式中:x为双圆柱的位移,m;A为振动的振幅,m;f为振动的频率,Hz;t为时间,s.

两圆柱的运动采用Fluent用户自定义函数UDF中的DEFINE-CG-MOTION定义,并结合动网格技术实现.

2 计算结果与场协同分析

2.1 不同间距比静止双圆柱的传热分析

笔者对不同Re下,间距比L/D=2.0～6.0的静止双圆柱进行了传热分析,并在数值计算后得到两圆柱面平均Nu(对整个圆柱面Nu积分的再平均)随间距比的变化曲线.图2为静止双圆柱面平均Nu随间距比的变化.从图2可知:在3种不同Re下,上游圆柱面和下游圆柱面平均Nu均在L/D小于3.5时较小,当L/D增大到3.5后平均Nu增大且随后趋于平稳.

图2 静止双圆柱面平均Nu随间距比的变化Fig.2 Average Nu number of the stationary twin cylinders varying with spacing ratio

限于篇幅,以下分析仅在Re=396时展开.图3为L/D=2.0～6.0时的流场结构.从图3可知:当L/D为2.0～3.0时,上游圆柱的分离剪切层均很明显,并附着在下游圆柱上,上游圆柱没有出现涡的脱落;当L/D增大到3.5后,上游圆柱开始出现涡脱落,并不断向下游圆柱甩出脱落涡,流场结构与L/D＜3.5的工况有很大不同.通过N-S方程可了解到:流场的改变必然会影响温度场,最终使双圆柱在不同间距下的速度场和温度场均发生变化,从而导致传热性能改变.因此,从流场和传热看,L/D=3.5是本文计算范围内静止双圆柱绕流时上游圆柱涡脱落与否及传热强弱的临界值.

流体绕流静止圆柱对流传热实验关联式如下[7]:

图3 L/D=2.0～6.0时的流场结构Fig.3 Velocity distribution contours for the cylinders with L/D=2.0-6.0

式中:Pr为水流温度时的普朗特数;Prsurf为圆柱表面温度时的普朗特数.

式(2)的适用范围为:Pr≤10,40≤Re≤1 000.

将静止双圆柱间距比L/D=2.5、Re=396时c1的数值模拟得到的Nu与实验关联式计算所得出的Nu进行比较,结果列于表1.从表1可以看出,数值模拟结果与实验关联式结果吻合较好.

表1 数值模拟结果与实验关联式计算结果的对比Tab.1 Comparison of results respectively obtained by numerical simulation and empirical formula

2.2 沿流向振动的双圆柱在不同间距比下的传热

图4为Re=396时,振动双圆柱面平均Nu随间距比的变化.由图4可知,振动双圆柱面平均Nu随间距比的变化规律与静止时类似.在L/D小于3.5时,圆柱面平均Nu较小,而在L/D达到3.5后,两圆柱面平均Nu增大,且随后随间距的变化Nu变化较小.

从图2和图4可知:当双圆柱振动或静止时,上游圆柱面和下游圆柱面平均Nu随着间距比的变化规律相似,且上游圆柱面平均Nu在各间距比下均大于下游圆柱面.从流场结构进行分析(图3),当定常来流的流体绕流上游圆柱c1后,流体的流动发生了变化,出现流体的回流并在间距比达到一定值后,上游圆柱面出现有规律的涡脱落,从而使下游流场分布状况发生了改变,其流速大小和方向均与流体横掠上游圆柱面时不同,使下游圆柱面所处的流场变为非定常流场,流场的改变最终影响温度场,导致下游圆柱面的平均Nu的大小发生变化.因此,在静止和振动条件(图2和图4)、各间距比下时,上游圆柱面与下游圆柱面的平均Nu不同,处于下游并受到c1尾流影响的下游圆柱面的平均Nu小于上游圆柱面.

图4 振动双圆柱面平均Nu随间距比的变化Fig.4 Average Nu number of the vibrating twin cylinders varying with spacing ratio

另外,本文所计算的不同间距下的双圆柱传热,由于相邻圆柱间的相互作用不可忽略,因而使两圆柱所处的流场和温度场与单圆柱绕流传热不同.因此,即使两圆柱面的平均Nu变化规律一致,均在间距比L/D超过3.5后,Nu增加,随后趋于不变,但在各间距比下,上游圆柱面与下游圆柱面的平均Nu并不相等,只是达到相对稳定.

当Re=396时,在静止和流向振动2种方式下,笔者对双圆柱传热面的平均Nu进行了比较,并计算了不同间距比下的振动强化传热百分比.传热百分比η利用下式求得:

式中:Nu振动为双圆柱沿流向振动时的圆柱面平均Nu;Nu静止为双圆柱静止时的圆柱面平均Nu.

图5为流向振动强化传热百分比随间距比的变化.在各间距比下,与静止时相比,流向振动使双圆柱面的平均Nu均有所提高,当L/D达到3.5后,强化传热百分比开始增大.在L/D取值范围为3.5～6.0时,各间距比的强化传热程度相近,均在170%左右.因此,与双圆柱静止绕流传热相比,两圆柱沿流向振动时,传热能力增强,且当间距比大于临界值后,传热强化程度提高且随间距比的变化不大.从图5还可看到:当两圆柱采取相同的振动方式时,在间距比达到一定值后,上、下游圆柱强化传热的百分比接近.

图5 流向振动强化传热百分比随间距比的变化Fig.5 Heat transfer enhancement for the oscillating cylinders varying with spacing ratio

2.3 场协同分析

过增元[8]提出的场协同理论表明:在其他物性参数不变的条件下,减小速度矢量与温度梯度的协同角可以增强传热.在研究过程中,笔者对Re=396时不同间距下上游圆柱面和下游圆柱面温度边界层内的流场和温度场进行了协同分析,并通过UDF编程技术[9],分别对静止和振动时上、下游圆柱温度边界层内的速度矢量和温度梯度的夹角β进行了计算,获得了静止与振动时协同角随间距比的变化曲线.协同角β可采用下式进行计算:

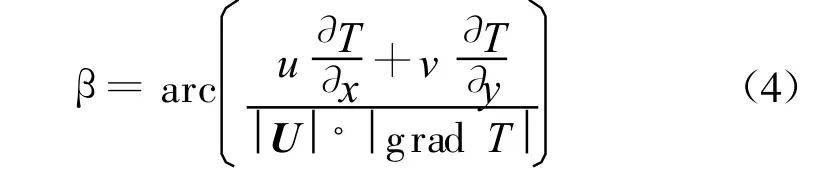
式中:u为流体沿x方向的速度值,m/s;v为流体沿y方向的速度值,m/s;T为流体的温度,K;β为速度矢量U与温度梯度的夹角,(°).

静止和振动时协同角的计算结果如图6所示.由图6可知:双圆柱在L/D达到3.5后,振动和静止时温度边界层内的协同角β均明显减小,且振动时减小的幅度约为20°;静止和振动时协同角的变化分别与图2和图4中Nu随间距比的变化相对应.当L/D＜3.5时,Nu较小,协同角β较大;当L/D达到3.5后,Nu增大,协同角β减小.从图6还可看出:在相同间距比下,振动时的协同角明显小于静止时的协同角.

图6 协同角随间距比的变化Fig.6 The synergy angles vs.spacing ratios

从场协同的角度进行分析,两圆柱的间距比不同会使速度场和温度场发生变化,从而导致速度场和温度场的协同程度不同以及传热不同.当间距比L/D小于3.5时,速度矢量与温度梯度夹角较大,场协同程度差,两圆柱面的平均Nu较小,传热较弱;当间距比L/D达到3.5后,速度矢量与温度梯度夹角减小,场协同程度提高,两圆柱面的平均Nu增大,传热能力增强.与静止相比,两圆柱的振动使流场和温度场均发生改变,协同角进一步减小,协同程度进一步改善,对流传热进一步得到提高.

因此,在对换热器进行强化传热设计时,在不改变管束排列数目的条件下,可以通过调整管束横向间距值和对管束施加振动的方式来提高对流传热性能,其中在层流条件下,管束横向间距与直径比值可以考虑取本文的临界值L/D=3.5.

3 结 论

(1)在不同Re下,L/D均存在一个临界值,当小于该临界值时,两圆柱面传热较弱;当L/D达到临界值后,两圆柱面传热增强且随L/D的变化不大.对双圆柱施加流向振动条件时,L/D的临界值不会改变.

(2)在相同L/D下,双圆柱的振动比静止条件下的传热性能明显增强,且在一定L/D范围内振动对传热的强化程度相近.

(3)场协同分析表明:在不同L/D下,速度场不同,速度场和温度梯度场的协同程度也不同.当L/D达到临界值后,协同程度提高,对流传热增强.两圆柱振动使速度场和温度梯度场的协同得到改善,双圆柱的传热性能增强.

[1] 刘松,符松.串列双圆柱绕流问题的数值模拟[J].计算力学学报,2000,17(3):260-266. LIU Song,FU Song.Numerical simulation of flow past two cylinders in tandem arrangement[J].Chinese Journal of Computational Mechanics,2000,17(3):260-266.

[2] FU Wushung,TONG Baohong.Numerical investigation of heat transfer from a heated oscillating cylinder in a cross flow[J].International Journal of Heat and Mass Transfer,2002,45(13):3033-3043.

[3] LEE Yongho,KIM Daehun,CHANG Soonheung.An experimental investigation on the critical heat flux enhancement by mechanical vibration in vertical round tube[J].Nuclear Engineering and Design,2004,229(15):47-58.

[4] 俞接成,李志信.流体低速绕流振动圆柱对流换热数值研究[J].工程热物理学报,2006,27(4):670-672. YU Jiecheng,LIZhixin.Numerical analysis on convection heat transfer of air f low across avibrating cylinder[J].Journal of Engineering Thermophysics,2006,27(4):670-672.

[5] ZDRAVKOCICH M M.Review of flow interference between two circular cylinders in various arrangement[J].Journal of Fluids Engineering,1997,28(3):183-200.

[6] 郑庭辉,费宝玲,杨骏六.串列双圆柱尾迹流的数值分析[J].西南交通大学学报,2008,43(6):747-750. ZHENG Tinghui,FEI Baoling,YANG Junliu.Numerical analysis of flow around two tandem circular cylinders[J].Journal of Southwest Jiaotong University,2008,43(6):747-750.

[7] ZHUAUSKASA.Heat transfer from tubes in cross flow[J].Advances in Heat Transfer,1972,15(8):116-133.

[8] 过增元.换热器中的场协同原则及其应用[J].机械工程学报,2003,39(12):1-9. GUO Zengyuan.Principle of field coordination in heat exchangers and its applications[J].Chinese Journal of Mechanical Engineering,2003,39(12):1-9.

[9] 胡汉波,李隆键,张义华.直接空冷凝汽器三维流场特性的数值分析[J].动力工程,2007,27(4):592-595. HU Hanbo,LI Longjian,ZHANG Yihua.Numerical analysis of 3-D flow characteristics of direct air cooled condensers[J].Journal of Power Engineering,2007,27(4):592-595.