数列上下极限的研究
2011-10-25王岩岩刘伟
王岩岩,刘伟
(周口师范学院数学系,河南周口466001)
数列上下极限的研究
王岩岩,刘伟
(周口师范学院数学系,河南周口466001)
上下极限概念是极限概念的延伸,它们在正项级数收敛性判别、求极限、证收敛等方面有着重要的作用.本文将给出有界数列与上下极限关系的一种新证法,并且更深层次的研究了上极限与数列极限收敛之间的关系.
数列;上极限;下极限
极限的概念是高等数学的一个最重要的理论组成部分,极限思想在数学中起着非常重要的作用,它是解决数学分析问题的一个强有力的工具.数列上下极限的概念是数列极限概念的延伸,也是数学分析中的重要概念.本文将给出上下极限的三种定义.数列上下极限有许多重要性质,这些性质在解决问题中有着非常广泛的应用,深入了解这些性质是学习数列上下极限的关键,也是解决问题的关键,数列上下极限的性质是对数列极限性质的拓展,也给解决问题打开了一个全新的视角.
本文给出数列上下极限的五条性质,这些性质参见文献[1,2,3,4,5,6],在文献[6]中利用区间套定理证明了性质1,然而这种方法较难理解,本文利用致密性定理和确界原理相结合来证明此性质,这种证明方法简单易懂.文中进一步讨论了上极限与数列极限收敛之间的关系.
1 数列上下极限的定义
定义1[5]有界数列{an}的上(下)极限定{an}的最大(小)聚点记
定义2[1]坌ε>0,N>0,当n>N时,总有an<A+ε;又子列{an}使ank>A-ε(K∈N),则有(=A);坌ε>0,N>0,当n>N时,总有an>a-ε;又子列{ank}使ank<a+ε(K∈N),则有
定义3[1]
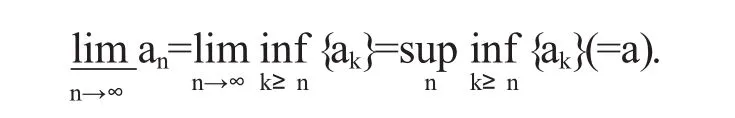
2 数列上下极限的性质
性质1[1]:有界数列{xn}必存在上极限和下极限.证因为{xn}为有界数列,由致密性定理:{xn}必存在收敛子列=a,则a为{xn}的聚点,即有界数列{xn}至少有一个聚点.记S为{xn}的聚点集合,坌s∈S,必存在,由于{xn}为有界数列,所以存在M>0,对坌n,有-M 性质2[2]:若{xn}是有界数列,则 推论:若数列{xn}收敛,则 性质3[4]:若有界数列{an}、{bn}满足:存在N0>0,当n>N0时,有an≤bn,则bn. 性质4[5]:{an}、{bn}是两列有界数列,若an≥0,bn≥0,n=1,2…则 性质5[2]:{an}为有界数列,若,则 由性质1知,当有界数列{an}的极限不存在,即有界数列{an}发散时,但数列{an}的上极限与下极限则一定是存在的.而文中推论则说明了当一个数列收敛时,它的极限值与上下极限间的关系.然而能否根据数列本身的结构及其上下极限来判别该数列的敛散性呢? 引理[5]:若an>0,n=1,2,…,则 当0≤a<+∞时,由数列极限定义知,坌ε>0,N>0当k>N时,有任取n>N,令k=N,N+1,…,n-1,将所得n-N个不等式相乘,由于k>N可得(a+ε)n-N圯an 〔1〕王振福,张建军.数列的上极限与下极限探析[J].包头职业技术学院学报,2008,3(1):12-14. 〔2〕许万银,齐小忠.数列上下极限问题的若干讨论[J].陇东学院学报(自然科学版),2009,13(1):68-71. 〔3〕钱佩玲.数列与上下极限[M].北京:北京师范大学出版社,2000:212-277. 〔4〕宛金龙,杨辉.数列上下极限的注记[J].安庆师范学院学报,2004,8(10):25-26. 〔5〕艾斯卡尔.阿布力米提.数列上下极限性质的推广应用[J].新疆教育学院学报,2003,11(19):26-34. 〔6〕华东师范大学数学系.数学分析上册第三版[M].北京:高等教育出版社,2001:23-34. O171 A 1673-260X(2011)01-0001-02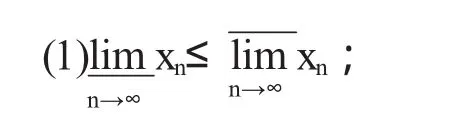
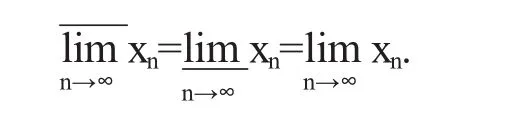

3 上下极限与数列敛散性之间的关系