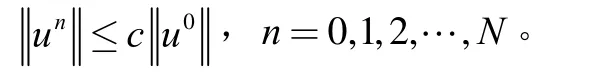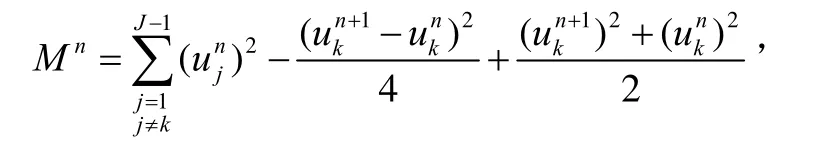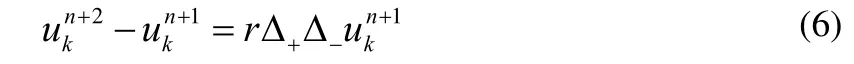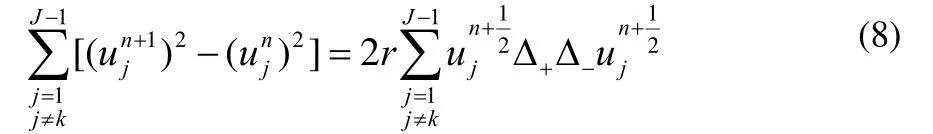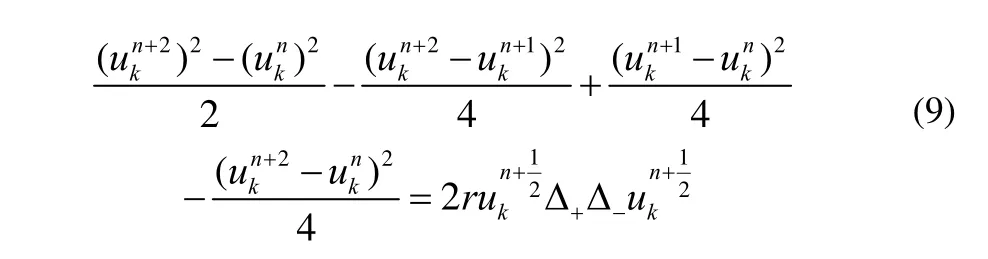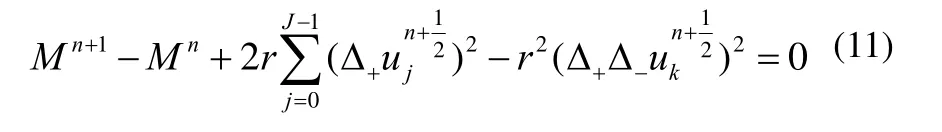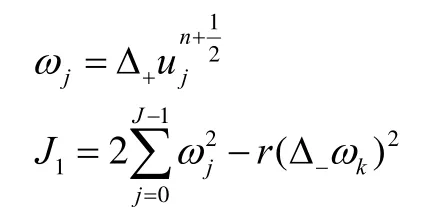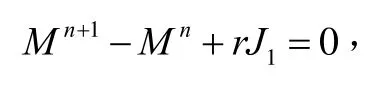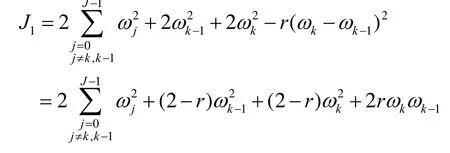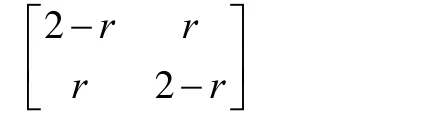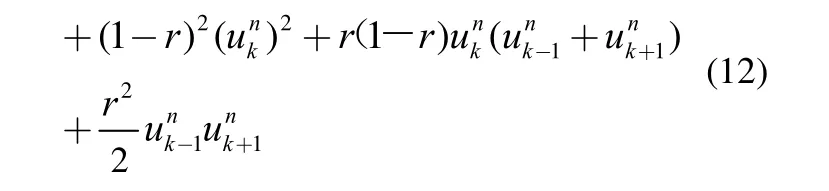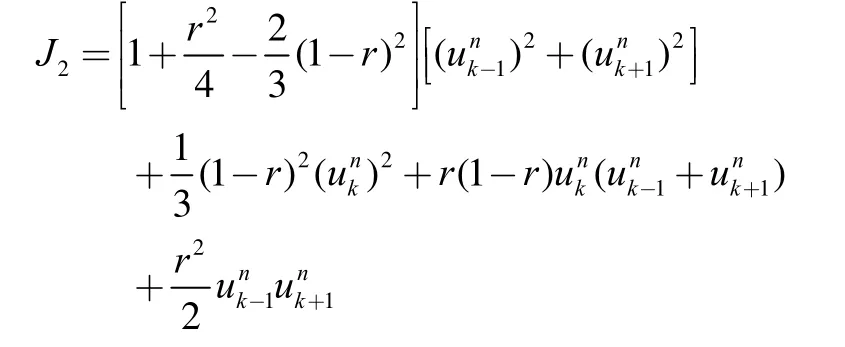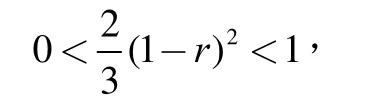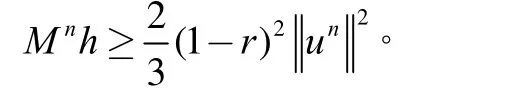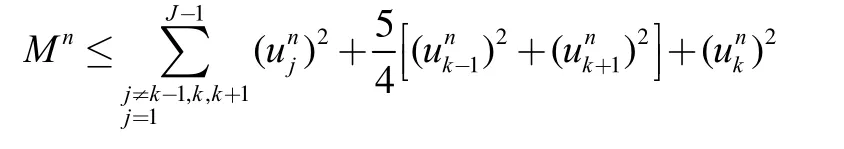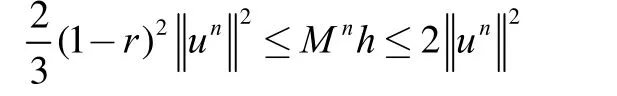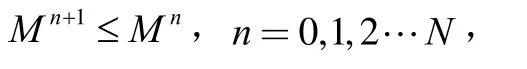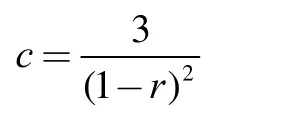热传导方程的C-N格式区域分解方法及其稳定性分析
2011-10-25任丽丽朱少红赵凤柱
任丽丽,朱少红,赵凤柱
(1.天津师范大学 数学科学学院,天津 300387;2.南开大学 数学科学学院,天津 300071;3.中国人民武装警察部队学院,河北 廊坊 065000)
求解热传导方程最常用的差分方法有古典显示、古典隐式和C-N格式[1]。从并行计算的观点看,古典显格式计算简单,便于编程,但这种格式是条件稳定的r≤1/2;古典隐格式和 C-N格式是绝对稳定的,但需要解整体的线性代数方程组,不能直接实现并行计算。有限差分区域分解算法综合了显格式和隐格式的优点,是一种高效实用的方法,目前已有很多关于区域分解方法的结果,文献[2]在内边界点使用大空间步长H=mh的古典显格式,在每个子区域内使用古典隐格式求解,发展了有限差分区域分解算法。本研究基于C-N格式,设计了一种新的并行差分格式,能进一步放宽稳定性约束条件,得到稳定性条件为r<1。
1 并行差分格式的构造
考虑热传导方程:
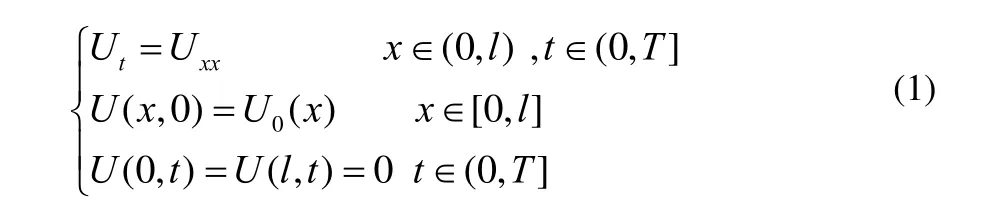
为了对初边值问题(1)作差分逼近,首先对求解区域作网格剖分:取空间步长h=l/J和时间步长τ=T/N,其中J,N都是自然数。用2族平行直线:
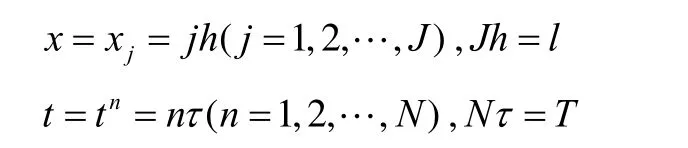
将求解区域{0 ≤ x ≤ l; 0 ≤ t ≤ T }分割成矩形网格,网格节点为(xj,tn)。记

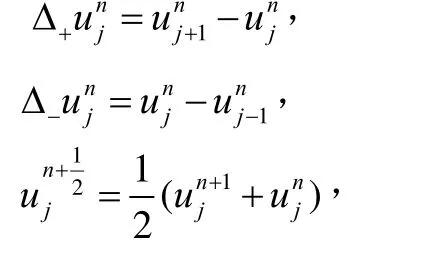
易知

定义离散L2范数(Euclid范数):

其中
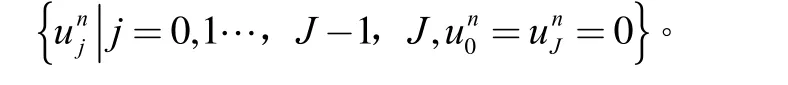
将问题(1)的求解区域[0,l]分解为2个子域[0,xk]及其中1 定理若 r=τ/h2< 1,则差分方法Ⅰ的数值解按离散L2范数关于初值稳定,即存在正常数c,使方法Ⅰ的任意解,均满足不等式: 为证明定理,先给出2个引理。 引理1设 则当0 证明由(3)得: 则[(3)+(6)]/2得 利用Mn的表达式,(8)+ (9)可整理为 将(7)代入(10)得: 记 则(11)可整理为: 易知若J1非负定,则 Mn+1≤Mn。 下面讨论J1非负定的条件。 直接计算可得当r<1时,矩阵 非负定,从而J1非负定,则当0 证毕。 引理2当0 证明将(3)代入 可得 进一步有: 其中 直接计算可知,当0 非负定,即J2非负定。又因为 故有 于是 另一方面,由于0 所以 从而 证毕。下面给出定理的证明。 由引理1,当0 由引理2知 即当0 取 于是定理成立。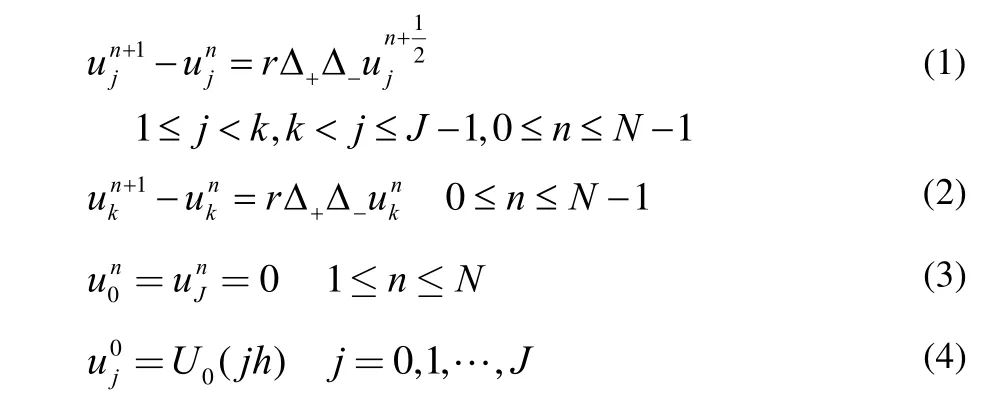
2 稳定性分析