凝聚环的扩展研究
2011-10-25张金羽
张金羽
(河南工业大学 理学院,河南 郑州 450052)
定义1设A为左R-模,若A为f.g.的,且A的每个f.g.子模为f.p.的,则称模A为凝聚模。
定义2设R为环,若R作为左R-模为凝聚的,则称R为左凝聚环。
类似地,可定义右凝聚环。
定义3令∏=∏RR为任意个RR的积,若∏的每个f.g.子模为f.p.的,则称环R为左Π-凝聚环。
类似地,可定义右Π-凝聚环。
定义4设R为环,令⊕=⊕RR为任意个RR的上积,若⊕的每个有限生成子模为有限表现的,即任一自由模的每个f.g.子模为f.p.的,则称R为左弱∏-凝聚环。
类似地,可定义右弱Π-凝聚环。
显然,Π-凝聚环为弱Π-凝聚环,而弱Π-凝聚环为凝聚环。
定义5一个模A称为弱余生成的是指它可嵌入一个自由模中,即有正合列0→A→RR(I),其中I为任意集合。
定理1设R为环,则下列陈述等价:
(1)R为左弱Π-凝聚环;
(2)每个f.g.弱余生成的左R-模为f.p.的。
证明(1)⇒(2)。设A为 f.g.弱余生成的左 R-模,即有正合列,从而A为⊕RR的f.g.子模,由左弱Π-凝聚环的定义,有A为f.p.的。
(2)⇒(1)。设A为⊕RR的f.g.子模,即A为弱余生成的,从而A为f.p.的,故R为左弱Π-凝聚环。
凝聚环和凝聚环上f.p.模的性质,对于弱Π-凝聚环和弱Π-凝聚环上的f.g.弱余生成模也成立。
命题1 设R为交换弱Π-凝聚环,若A和B为f.g.弱余生成R-模,则HomR(A,B)为f.g.弱余生成的。
证明因A为f.g.弱余生成R-模,由定理1可知,A为f.p.的,从而有R-模的正合列

其中 F1,F0为 f.g.自由模,由于函子 HomR( -, B)为左正合反变函子,故有正合列

而

由正合列

其中 HomR(F0,B )。Imφ*为 f.g.的,从而 HomR(A ,B)为f.g.的,而 HomR(F0,B)为弱余生成的, HomR(A,B)为它的子模,故 HomR(A,B )为f.g.弱余生成的。
命题2设R为交换弱∏-凝聚环,若A,B为f.g.弱余生成R-模,则和为f.g.的。
证明因A为f.g.弱余生成R-模,R为弱Π-凝聚环,故A为f.p.的,从而有R-模的正合列

其中每个Fi为f.g.自由模。
从而有复形
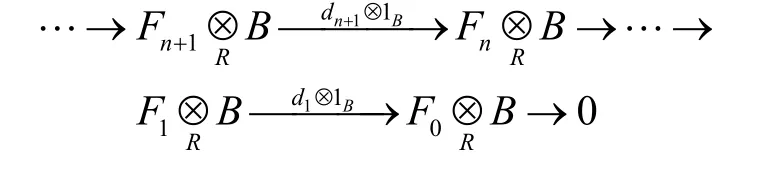
故

因

B为f.g.弱余生成的,故 B(m)为f.g.弱余生成的,即为f.g.弱余生成模,又 R为弱Π-凝聚环,从而为 f.p.的,∀i≥0考虑正合列

命题 3设 R为左弱Π-凝聚环,A为 f.g.弱余生成左R-模,n(≥-1)为整数,则下列陈述等价:
证明(1)⇒(2)显然。
(1)⇒(2)。对结论(2)采用数学归纳法证明。
若 n=-1,由(2)有 HomR(A ,B) = 0,其中B为任意f.g.弱余生成左R-模,故 HomR(A ,A) = 0,从而有A=0,所以l.P dRA=-1。
若n=0,显然A为f.p.的,故有R-模的正合列

其中F为f.g.自由模,k为f.g.弱余生成左R-模,因此由(2)及上同调长正合列定理有正合列

若n≥1,类似地,有正合列

而F为自由模,B为f.g.弱余生成模,故

由归纳法假设有

另由正合列

可知 l. PdRA ≤ n.证毕。
定义6 设R为环,若对任意f.p.左R-模A都有

定理2环R为左弱FP-内射环⇔每个f.p.右R-模为弱余生成的。
推论1设R为左弱∏-凝聚,左弱FP-内射环,A为任意f.g.弱余生成左R模,则下列陈述等价:
(1) l.P dRA ≤ n ;
证明(1)⇒(2)。由于左弱Π-凝聚环R上f.g.弱余生成左 R-模为 f.p.的,从而由凝聚环的性质有l.fdRA=l.P dRA,故当 l. PdRA ≤ n 时,必有,对

知R/I为 f.p.的,从而由定理 2知R/I为 f.g.弱余生成右R-模,故由(2)又有

(2)⇒(1)。对任意f.g.右理想,由正合列
