基于局部多项式回归方法的抽样估计

陈光慧

（暨南大学 经济学院，广州 510632）

基于局部多项式回归方法的抽样估计

陈光慧

（暨南大学 经济学院，广州 510632）

在辅助信息可利用的情况下，文章研究了有限总体总值的估计问题。首先回顾了Horvitz－Thompson估计量和广义回归估计量；然后指出当辅助变量与研究变量不满足经典线性回归模型假设时，可建立非参数回归模型，运用局部多项式回归估计的方法进行估计；最后，引入了一个实际例子，并对估计结果进行了比较。

辅助信息；抽样估计；非参数回归模型；局部多项式回归估计量

0 引言

在很多抽样问题中，我们往往希望能得到一些辅助信息，利用这些辅助信息来提高抽样估计的精度。这些辅助信息主要包括普查资料、政府部门的行政记录和有关企、事业单位的生产业务记录以及以前所搜集的调查资料等等。对于已经得到的辅助信息，我们可以从不同的角度进行利用。具体地说，可以在抽样设计阶段利用辅助信息，也可以在抽样估计阶段利用辅助信息。

在抽样设计阶段利用辅助信息，主要是指不等概率抽样（包括PPS抽样和πPS抽样等等）。比如说，在πPS抽样中，研究变量y与已知的辅助变量x呈一定的相关关系。我们可以在抽样设计阶段利用这种相关关系，令第i个总体单元被包含到样本中的概率，即入样概率为

这样，如果根据抽样设计p(·)，从总体U中抽出一个概率样本s，那么就可以得出未知总体总值ty=∑Uyi的无偏估计量，也就是Horvitz－Thompson估计量

且Horvitz－Thompson估计量的方差为

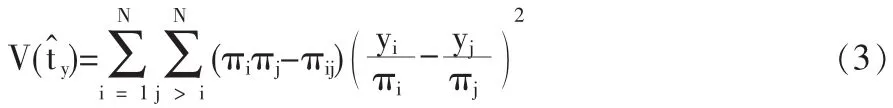
这里的 πi如式（1）所示，πij即为第 i和 j两个总体单元同时入样的概率。 观察式（2） 和式（3）可知，估计量t赞y及其方差公式中没有出现辅助变量。也就是说，仅仅在抽样设计阶段利用了辅助信息，在抽样估计阶段没有利用辅助信息。S覿rndal等人（1992）已经证明，在抽样估计阶段利用辅助信息（即辅助变量进入估计量公式中），往往能得出比Horvitz－Thompson估计量更有效的估计量。

在研究抽样估计阶段如何利用辅助信息时，首先往往假定一个超总体线性回归模型

来描述研究变量y与辅助变量向量x=(x1,…,xK)'之间的关系，而把需要调查的未知研究总体U（即{yi,xi}）看成是这个超总体线性回归模型的一次具体实现，其中x1,…,xN是辅助向量x的值。若用研究总体数据来估计模型参数，可得参数β的最小二乘估计量为

但是由于在实际调查中，总体是未知的，所以不能直接用来估计模型参数β，我们只能从总体U中抽出一个样本s（即{yi,xi}），利用样本s的信息以及辅助变量向量x的总体总值tx=∑Uxi=(t1,…,tK)'来估计模型参数，进而得出总体总值ty=∑Uyi的估计量。Sarndal等人（1992）基于此模型提出了广义回归估计量（简称GREG估计量），公式

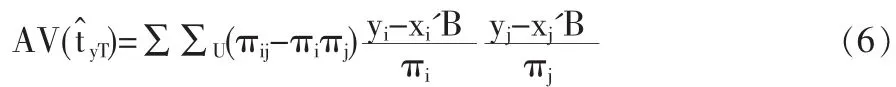
此估计量是ty=∑Uyi的渐进无偏且一致估计量。一般来说，式（5）中的广义回归估计量比式（2）中的 Horvitz－Thomp-son估计量更优。

在以往关于回归估计的研究中，我们很少考虑建立的回归模型是否满足经典线性回归假设。虽然，S覿rndal等人（1992）提出的广义回归估计量考虑到了异方差的问题，但对于实际中真实的数据来说，仅仅这样可能还不够，还有很多模型设定误差需要考虑，甚至实际数据是否呈线性关系还需要研究。如果从这方面考虑，那么基于上述线性回归模型得出的估计量的精度可能没有想象中的理想。针对此问题，本文拟建立非参数回归模型，并提出局部多项式回归估计的方法。

1 局部多项式回归估计量的基本思想

非参数回归模型的特点是回归函数的形式可以任意，不受任何约束，因而具有较大的适应性。近几年，国外有些学者已经开始把非参数模型引入到抽样理论研究中，比如，Breidt和Opsomer(2000)等人提出模型辅助条件下的各种非参数估计量。对于非参数回归模型，本文使用局部多项式回归方法进行估计，局部回归的优点是假定变量之间的关系未知，没有隐含任何假设条件，所以更加符合实际情况。

局部回归的主要思想是，对于给定的x，认为模型回归函数m(.)在x附近的局部领域近似于线性，对x附近的那部分数据应用线性回归技术，而该局部领域的大小由窗宽（记为h）的大小来控制。

2 局部多项式回归估计量的构建过程

为了简化问题，本文以一个辅助变量的一元回归模型为例介绍局部回归估计，有多个辅助变量的情形可以类似考虑。

第一步，建立如下无限超总体非参数回归模型ξ

其中xi是已知的辅助变量；yi是未知的研究变量；εi是独立的随机误差项，且其均值为0，方差为v(xi)；m(x)是关于x的一个光滑函数，其表达形式未知。在给定xi情况下，模型ξ也可以表达为如下形式

与第一节中的线性回归模型ζ一样，我们把需要调查的未知总体U（即{yi,xi}Ni=1）看成是这个超总体非参数回归模型ξ的一次具体实现。但是由于总体是未知的，所以不能直接进行估计，我们只能从总体U中抽出一个样本s（即{yi,xi}ni=1），利用样本s的信息以及辅助变量x的总体总值tx=∑Uxi来估计非参数回归模型，进而得出研究变量总体总值的估计量。

第二步，假定函数m(x)在x=xi处p+1阶导数存在，则可以对m(x)在x=xi处进行泰勒级数展开，表达如下

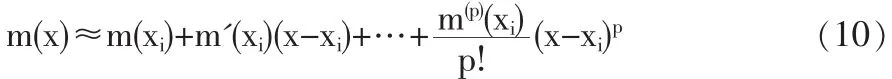
对于样本资料{yk,xk，我们有

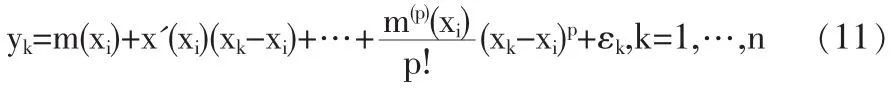
对上面的多项式运用加权最小二乘法进行局部拟合。假定控制局部领域大小的窗宽为h，则对于xi的领域 (xi-h,xi+h)，有

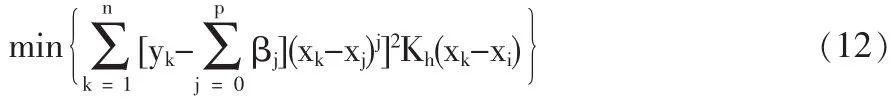
其中 Kh(·)=K(·|h)/h，K(·)为核函数，h 为窗宽。 为了方便进一步讨论，把式（11）表达成矩阵的形式为

其中

这里的β为参数向量，且βv=m(v)(xi)/v!,v=0,1,…,p；ε为模型误差向量。

通过极小化

β的加权最小二乘估计为

其中 Wsi=diag{Kh(xk-xi)}；k=1,…,n。 由于 βv=m(v)(xi)/v! （v=0,1,…,p），可得式（8）中 m(xi)的样本估计值为

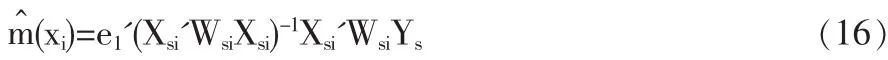
这里 e1=[1 0 … 0]'（p+1）×1。 即等于向量β赞中的第一项。

第三步，采用式（5）中广义回归估计量的形式，可得总体总值ty=∑Uyk的局部多项式回归估计量为

与式（6）中近似方差公式类似，可得局部多项式回归估计量的近似方差公式为

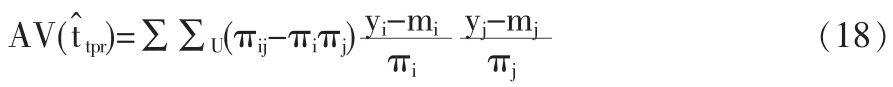
其中mi=e1'(X'UiWUiXUi)-1XUi'WUiYU是用总体数据去估计非参数回归模型时得出的关于m(xi)的估计值。推导方法与推导式（16）的样本估计值一样。同理，与式（7）类似，得出近似方差的估计量为

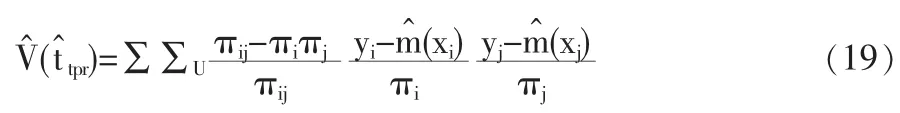
其中，m赞(xi)=e1'(Xsi'WsiXsi)-1XsiWsiYs。

3 数值分析

为了更好地说明局部多项式回归方法在抽样估计中的应用，我们引入一个实际例子进行分析，即估计广东省某年的粮食总产量。按照行政区划将广东省分成89个县 （市）、区，即总体单元总数N=89；研究变量表示第i个地区的粮食产量；另外，选用与研究变量高度相关的常用耕地面积作为辅助变量，因为各个地区不同年份常用耕地面积很少变化，其数据可通过往年的统计年鉴得到，且用xi表示第i个地区常用耕地面积，其中i=1,…,89。目标是估计总体总值，即广东省粮食总产量ty=∑Uyi，为此抽出一个样本量n=30的样本进行估计。为了简化问题，这里使用简单随机抽样得出样本量为30的样本，样本数据在此略过。

从样本中得到了30个样本单元的研究变量值 （即粮食产量yi,i=1,…,30），且还知道总体的辅助变量值（即常用耕地面积xi,i=1,…,89，通过以往的资料或普查可获得）。下面的任务就是利用这些信息来估计总体总值 （即广东省粮食总产量）。

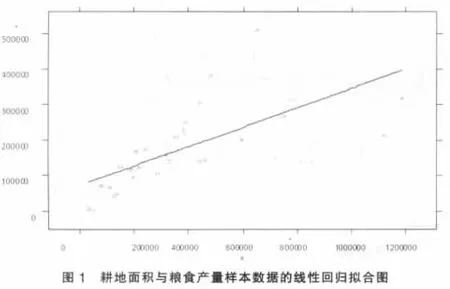
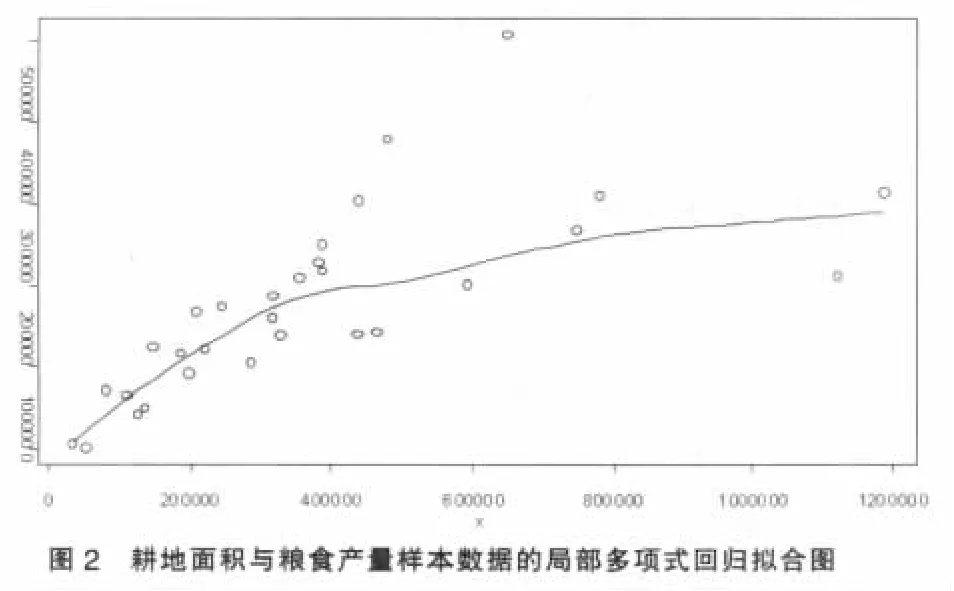
一般来说，这里可以利用辅助变量的信息进行回归估计。但是通过观察图1和图2中的两条回归趋势线，可以发现，由于30个样本点呈线性回归趋势并不明显，若强行进行线性回归估计，其效果可能很差。但是，图2中的局部多项式回归拟合图拟合效果较好。下面分别进行线性回归估计和局部多项式回归估计，并对两种方法的估计精度进行比较。

由于使用简单随机抽样，那么包含概率相应为

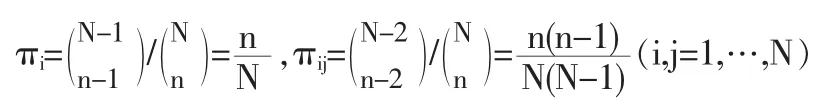
且进行局部多项式回归估计时，选择核函数K(u)=0.75(1-u2)I(|u|≤1)，其中 I(·)为示性函数，当括号内的不等式成立时，取值为1；否则取值为0。确定窗宽h=0.8。运行MATLAB 7可得出结果如表1。

表1 两种估计方法的结果

从表1中可发现，两种估计方法中，由局部多项式回归方法得出的估计量的近似方差更小，因而估计得更加精确。

4 结束语

本文研究了在辅助信息可利用的情况下，有限总体总值的估计问题。文章回顾了Horvitz－Thompson估计量和广义回归估计量及存在的问题，当辅助变量与研究变量不满足经典线性回归模型假设时，考虑建立非参数回归模型，并运用局部多项式回归估计方法进行抽样估计，构建局部多项式回归估计量。最后，引入了一个实际例子进行分析，显示了该估计量的准确性。

[1]冯士雍，倪加勋，邹国华.抽样调查理论与方法[M].北京：中国统计出版社，1998.

[2]李子奈，叶阿忠.高等计量经济学[M].北京：清华大学出版社，2000.

[3]叶阿忠.非参数计量经济学[M].天津：南开大学出版社，2003.

[4]W.G.Cochran.抽样技术[M].张尧庭，吴辉译.北京：中国统计出版社，1985.

[5]Breidt,F.J.，Opsomer,J.D.Local Polynomial Regression Estimators in Survey Sampling[J].The Annals of Statistics,2000,(2).

[6]Sarndal E.C.,Swensson B.,Wretman J.Model Assisted Survey Sampling[M].New York:Springer,1992.

C811

A

1002－6487（2011）04－0003-03

全国统计科学研究重大项目（2009LD001）

陈光慧（1980-），男，安徽旌德人，博士，讲师，研究方向：统计调查与数据分析。

（责任编辑/亦 民）