带有反馈和不耐烦的双端排队系统
2011-10-24单净璇朱翼隽濮华盛
单净璇,朱翼隽,濮华盛
(江苏大学理学院 数学系,江苏 镇江 212013)
带有反馈和不耐烦的双端排队系统
单净璇,朱翼隽,濮华盛
(江苏大学理学院 数学系,江苏 镇江 212013)
文章以需求/供应系统为背景,研究了带有反馈和不耐烦的双端排队模型。假定供应方d到达系统服从泊松分布,需求方到达系统的时间间隔服从一般分布,利用补充变量法构造马尔可夫过程,通过状态转移分析列出微分方程,借助概率母函数求出该系统的一些性能指标。
双端;补充变量法;概率母函数;L变换
0 引言
双端排队模型最早是由Kendall[1]提出的,他初步设想了乘客与出租车都以possion流到达车站时的问题,其中乘客与出租车数量均无限。之后被许多不同的作者研究过。Dobbi[2]在kendall基础上引入了时间函数的概念,Jain[3]进一步讨论了当出租车等待空间是有限(不多于n)的情形,而Kashyap[4-6]系统研究了出租车与乘客等待空间均有限的双端排队模型并讨论了出租车分布是k阶Erlang分布的特殊情形。近年来国际上B.W.Conolly[7]讨论了双端排队在通讯网络以及编程语言上的应用。国内尹小玲,苏健[8]考虑了引入负顾客的等待空间有限的双端排队系统。
与此同时,双端排队模型在需求/供应系统中有着广泛的应用背景,其中库存生产模型可以理解为双端排队模型的扩展。库存问题的研究最早可追溯到1915年Harris所首先建立的著名的经济批量公式 (Economic Order Quantity,EOQ)。研究库存系统需要解决的问题通常是,确定系统的最优控制变量,以使费用目标函数达到最小。Berman,Kaplan及shimask[9]研究了需求率是常数,订货瞬时到达的库存系统。Berman和Kim研究了需求服从指数分布,所订货物的到达有一个延迟的库存系统,He Q M[10]等人利用排队论的矩阵几何解的理论,给出了库存系统中的每件产品的平均费用函数的2个算法,侯玉梅[11]等人在此基础上进行了简单生产-库存系统的优化控制。
带反馈的排队系统与经典排队系统不同,其服务机制有所变化,顾客到达系统后并不一定依次服务就离开系统,而是有可能经过多次,这个服务次数是由反馈机制所决定的[12-14],其中主要的Bernoulli反馈已被广泛应用于计算机分时操作和无线电通讯网络系统中,通过对它一些指标的研究,可安排最合理的运行管理方案[15]。
在很多实际服务系统中会有不耐烦顾客出现,产生不耐烦顾客一般有两种情况:一是顾客刚刚到达时,因其不能被马上服务而立刻离开系统,称之为阻滞;二是顾客到达并进行排队,排队一段时间以后失去耐心,未等到服务即离开系统,称之为中途离开。
综上所述,本文讨论一个带有反馈和不耐烦的双端排队系统,比如对于库存系统这个由仓库和顾客共同构成的双端排队系统中,到达的顾客随时有可能会因为不耐烦而离开系统。同时,顾客方并不是依次进行服务后立刻离开系统,而是有可能需求得到满足后发现货物质量有问题需要调换等问题而要求再次服务,这就要由反馈机制决定。
1 模型的描述
由一个仓库和顾客共同构成的双端排队系统中,需求与供应之间的关系体现在仓库库存的增加与减少。此时需求方相当于顾客,而供应方相对于需求方可以看做是提供服务的服务员,其服务率为供应方的到达率,服务规则是先到先服务。供应方(服务端)以参数为λ的泊松分布到达系统,需求方(顾客端)到达系统的时间间隔服从一般分布函数A(x),对应密度函数为a(x),L-S变换为A*(x),一阶矩、二阶矩为v1.v2。μ(x)表示相应的风险率函数,即有,若顾客到达发现系统中没有顾客则立刻接受服务,否则会有顾客因为等待不耐烦而离开(即中途离开情形)。离开前等待的时间η是一个随机变量,我们假设它服从参数为b的负指数分布。服务完成后以概率1-q反馈到队尾寻求再次服务或者以概率q离开。设库存量的等待空间为M,即第M+1个顾客到达则自动离开系统,同理顾客数的等待空间为N。若仓库中没有储备货物而有顾客到达时,系统将该需求记录为一个单位的缺货。为了保证生产持续进行及减少缺货事件的发生,仓库要向供应系统订货,以补充生产消耗。
我们进一步记系统中顾客数与库存数分别为U(t)和V(t),则系统中的队长为 N(t)=U(t)-V(t)=n(n=-M,-M+1,…,-1,0,1,2,…,N),当 n>0 时,表示时刻 t系统中有 n 个顾客在等待服务,当n<0时,表示时刻t系统中的库存量为|n|,n=0表示t时刻系统为空。显然{N(t),t≥0}不是马尔可夫过程,引入补充变量ξ(t)为时刻t与t前最后一个顾客到达时刻的时间间隔。于是过程{N(t),ξ(t),t≥0}形成一个马尔可夫过程。
2 模型求解
我们定义

通过状态转移分析,可以得到下列微分方程:
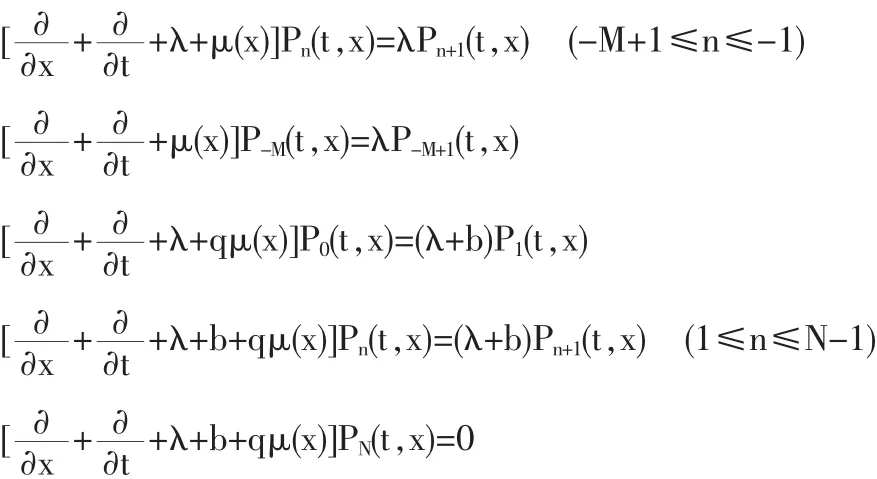
边界条件:
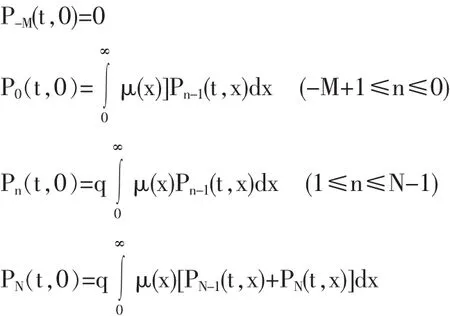
对上述方程作L变换可得:
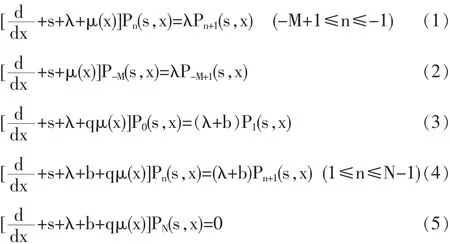
边界条件:
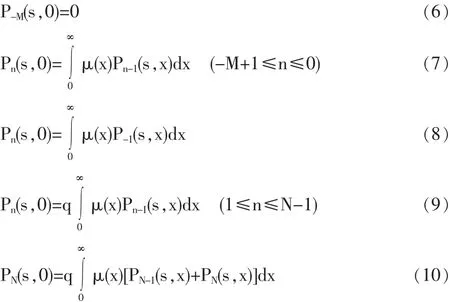





3 若干性能指标
通过以上的结果和算法过程,我们可以得到关于系统的以下几个性能指标:
(1)系统中有顾客的概率的L变换为:


[1]DG Kendall.Some Problems in the Theory of Queues[J].J.R.Statis.Soc.B,1951,13.
[2]JM Dobbie.A Double-ended Queueing Problem of Kendall[J].Ops Res,1961,9.
[3]HC Jain.A Double-ended QueueingProblem[J].Def.Sci.J,1962,12.
[4]BRK Kashyap.The Random Walk with Partially Reflecting Barriers with Application to Queueing Theory[J].Proc.Nat.Inst.Sci.India,A,1965,31.
[5]BRK Kashyap.A Double-ended Queueing System with Limited Waiting Space[J].Proc.Nat.Inst.Sci.India,1965,31A.
[6]BRK Kashyap.Further Results for the Double Ended Queue[J].Metrika,1967,11.
[7]BW Conolly,P R Parthasarathy,N Selvaraju.Double-ended Queues with Impatience[J].Computers and Operations Research,2002,29.
[8]尹小玲,苏健.带有负顾客的双端排队系统[J].中山大学学报(自然科学版),2004,43.
[9]Berman O,Kapla E H,Shimask D G.Deterninistic Approximations for Inventory Management at Service Facilities[J].I I E Transactions,1993,25.
[10]He Q M,Jewkes E M.Performance Measures of a Make-to-order Inventory-production System[J].Commun Statist-stochastic Model,2000,16.
[11]侯玉梅.简单生产—库存系统的优化控制[J].系统工程理论与实践,2003,(4).
[12]孙荣恒.排队论基础[M].北京:科学出版社,2002.
[13]余玅妙,唐应辉.反馈次数服从几何分布的M/G/1排队系统的队长分布[J].电子学报,2007,35.
[14]陈佩树,朱翼隽,王晓春.有反馈,强占型的M/G/1重试排队系统[J].统计与决策,2006,(9).
[15]B K Kumar,S P Madheswari.The M/G/1 Retrial Queue with Feedback and Starting Failures[J].Applied Mathematical Modelling,2002,26.
(责任编辑/亦 民)
O226
A
1002-6487(2011)03-0077-05
江苏大学研究生创新计划项目(CX10B-003X)
