基于看跌期权契约的应急物资采购储备模型
2020-04-13扈衷权冯耕中
扈衷权,田 军,冯耕中
(1.西安电子科技大学经济与管理学院,陕西 西安 710126;2.西安交通大学管理学院,陕西 西安 710049)
1 引言
应急物资是政府妥善处理突发灾害事件,降低损失,维护社会稳定的重要保障。与一般商业物资不同,应急物资具有需求发生概率小,需求量大,需求量不确定,缺货成本大,时效性强等特点,一般都是由政府事先采购,以实物形式进行储备,从而保证在灾害事件发生时,可通过全国应急物资储备网络,在第一时间将应急物资调往事发地点,防止灾害的进一步扩大,最大限度的保障人民生命和财产安全。因此应急物资的管理与追求零库存的商业物资管理有很大不同之处,即政府必须储备一定数量的物资,才可做到有备无患。然而,由于应急物资需求的发生概率较低,针对食品药品等一类具有一定保质期限的物资,特别容易出现应急物资到达保质期限后还没有使用的情况,这样不仅造成物资的浪费,同时也加重了政府的财政负担。因此如何在满足应急物资需求的同时,更有效地节约资源,提高应急物资管理的综合效率成为政府急需解决的问题之一。为此,本文借用供应链契约思想,建立了一种基于看跌期权契约的应急物资采购储备模型用以解决这一难题。
由于供应链契约能够消除双重边际效用,实现风险共担,信息共享,提高采购方与供应方的收益,近年来,已有很多学者将供应链契约理论应用于应急物资的采购中。Beamon和Kotleba[1]研究在有多个供应商供应应急物资的情况下,政府如何决定最优采购量的问题。Qi等[2]在假设需求为线性函数的基础上,针对突发事件所带来需求规模的变化,利用数量折扣契约来解决突发事件下供应链的协调问题。Lodree和Taskin[3]研究了需求发生变化的报童模型,用以评价由于供应链中断所带来的风险和收益。
近几年,一些借助于金融思想的新式契约开始兴起,其中最典型的代表就是期权契约。Ritchken和Tapiero[4]认为如果将金融领域中的期权概念加入到供应链契约中,则可有效提高供应链柔性,增强供应链成员之间的合作,更好地达到收益共享,风险共担的目的,因此越来越多的学者对期权契约展开了研究,并已将其推广到企业的日常采购中[5-6]。Barnes-Schuster等[7]较早地将期权的思想引入供应链契约的研究当中,通过期权契约研究了两阶段需求具有相关性的供应链协作过程。Cachon[8]则通过研究发现期权契约是回购契约与数量柔性契约的组合。随后有关期权契约的研究开始不断深入。Gomez-Padilla和Mishina[9]将期权契约扩展到多个供应商和单个零售商组成的供应链中。李建斌和杨瑞娜[10]考虑了现货市场供应有限且现货市场采购价格与需求相关情况下,零售商采用期权契约时的最优决策问题。而尤晓岚等[11]则考虑了现货市场具有流动性约束以及供应商生产能力约束时,供应商与零售商的均衡策略问题。以上研究的对象均为单向期权,还有的学者对双向期权契约展开研究[12-14]。
由于期权契约相比较于传统契约更具柔性,因此一些学者开始将期权契约应用于应急物资的采购储备管理中。田军等[15-18]基于期权契约建立了以政府为主导的应急物资采购储备模型,分别对实物储备和生产能力储备下的应急物资采购储备问题进行了研究。陈涛等[19]利用期权契约,研究了应对突发事件的社会化储备体系中,协议企业基于自身利益最大化为目标的实物储备与生产能力储备的协调性问题。Wang Xihui等[20]在考虑运输成本与库存成本的情况下,将期权契约与回购契约进行了比较,发现期权契约能够降低物资的运输成本,并给出了供应链达到协调状态时期权契约的设计方案。上述学者主要研究了有关应急物资采购量或储备量决策,还有一些学者则对应急物资的采购定价问题进行了研究。例如,Liang Liang等[21]基于期权二叉树模型对应急物资的采购定价问题进行了研究,Rabbani等[22]则在此基础上,进一步考虑了灾害强度对应急物资采购定价的影响。
然而,以上研究均是基于看涨期权契约所建立的应急采购机制,其对应的储备形式为企业实物储备或生产能力储备。虽然应急物资企业储备模式可利用企业在物资管理方面的经验,有效降低物资的库存成本,并有助于物资的轮换更新,但其保障程度与时效性方面要弱于政府储备,因此比较适用于重要程度相对较低或存储空间较大的物资,如帐篷,棉被,简易厕所等,而像食品医药品等这类重要程度较高且需求紧急的物资,政府储备模式则更为适合。然而,由于应急物资需求的发生概率较低,且食品药品等具有一定保质期限,因此极容易出现物资达到保值期限但还未使用的情况,而这将导致大量人力,物力和财力的浪费。虽然利用回购契约能够很好的解决这一风险,降低政府损失,但供应方并没有因为承担额外风险而获得补偿,若到期后政府剩余物资量较大,则势必将损害供应方利益。因此本文将借用期权思想,研究如何利用带有期权性质的回购契约——看跌期权契约来协调政府与供应方之间的利益关系,即政府通过支付额外权利金的方式来补偿供应方承担的风险,继以实现双赢的局面。
看跌期权契约与看涨期权契约相同,都需要采购方在期初向供应方支付一笔权利金,不同的是在看涨期权契约中,采购方有权要求供应方按照契约中约定的价格供应不超过约定数量的产品;而在看跌期权契约下,采购方将有权要求供应方按照约定的价格回购不超过约定数量的剩余物资。现阶段,与看涨期权契约相比,有关看跌期权契约的研究较少。Eppen和Iyer[23]最早将看跌期权的思想引入到供应链契约的研究中,并设计出一种新式契约——备份契约。Chen和Parlar[24]将看跌期权引入到单周期的采购模型中,并给出了采购方最优采购决策。梁罗和盛方正[25]则将期权的思想引入回购契约的研究当中,并与普通回购契约下的采购方最优决策进行了比较。
由于现阶段有关看跌期权契约的研究较少,且其契约形式适合解决食品药品等这类物资的保质期风险问题,因此本文在前人研究的基础上,将看跌期权契约应用于这类应急物资的采购储备管理中,探究政府在看跌期权契约下的最优采购储备决策,并进一步研究此时供应链协调及契约参数的设置问题。此外,本文还将与基于回购契约的采购储备模式进行对比分析,证明看跌期权契约的优越性。因而本文的研究不仅补充了现有供应链契约理论的不足之处,同时还扩展了政府应急物资的采购方式,具有较强的理论意义和实际应用价值。
2 模型描述
2.1 问题描述
采购方(政府)为有效应对突发事件,需要事前采购一定数量的应急物资进行储备。然而由于突发事件的发生是一个小概率事件,针对食品药品这类具有保质期限的应急物资,极容易出现到期后大量物资剩余的情况,这不仅造成物资的浪费,而且加重了政府的财政压力。为了使采购方和供应方共担风险,采购方将与供应方签订一份看跌期权契约,约定采购方在期初向供应方支付一笔期权费用,当一个契约周期结束之后,采购方有权要求供应方按照契约中约定的价格回购不超过约定数量的剩余物资,这样采购方不仅能降低自身成本,而且补偿了供应方所承担的风险,从而实现双赢。
2.2 基本假设
为了更好地反映看跌期权契约对采购方决策的影响,现做出如下假设:
(1)供应链包含一个采购方和一个供应方,采购方从供应方处采购一定数量的应急物资并储备在自身的储备库中,同时还会与供应方签订看跌期权契约;
(2)应急物资的需求发生是一个小概率事件。假设基于以往的历史数据,可以确定一个应急物资的最大需求量,其需求的概率分布函数可估测[15-18]。
(3)本文研究的对象主要为食品药品等这类重要程度较高,但具有一定保质期限的物资。如果在保质期内没有需求发生,则需要对其进行更新。为了防止物资完全浪费,假设应急物资的轮换周期小于其保质期,当一个周期结束之后,采购方和供应方将会把剩余物资按照残值进行出售;
(4)采购方与供应方之间信息完全对称,并且均为完全理性的决策者;
(5)与一般商业供应链不同,因应急物资所产生的社会收益无法可靠估计,故假设采购方的决策目标为自身成本最小[15-18]。
2.3 符号说明
本文所涉及的变量及其说明如表1所示:

表1 相关变量及其说明
同时,为了避免得到不合理的结果,假设相关参数之间的关系如下:
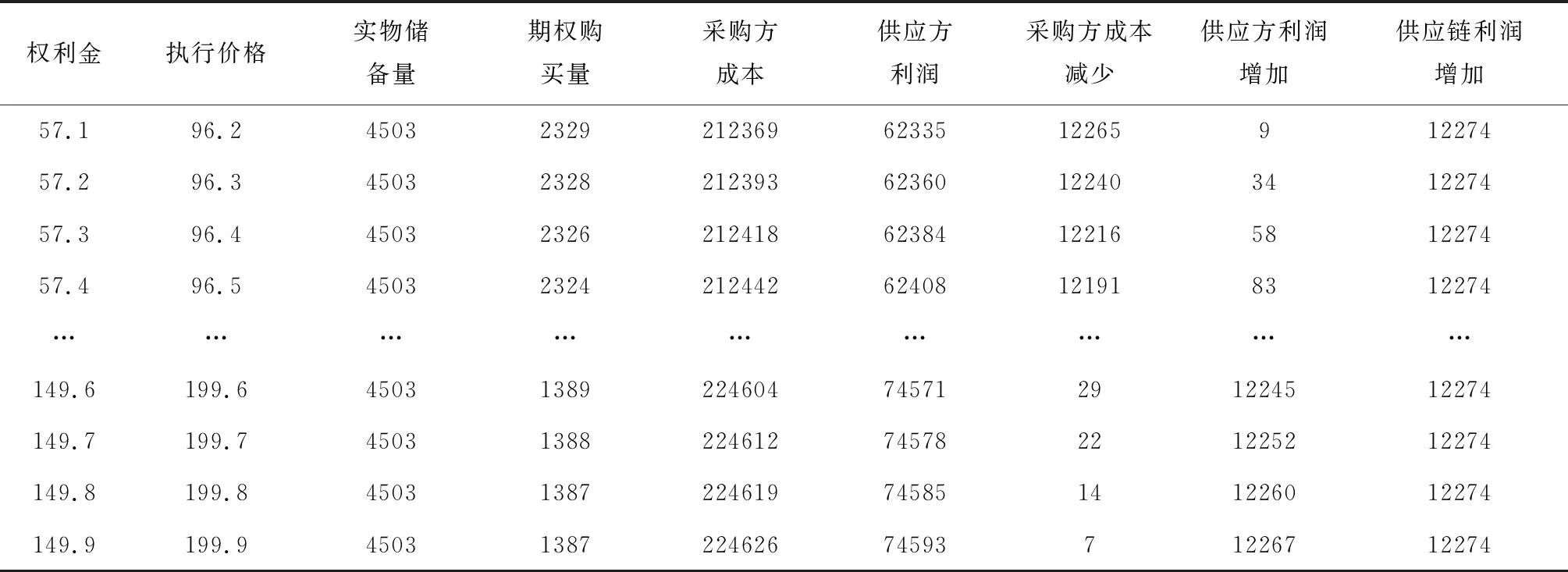
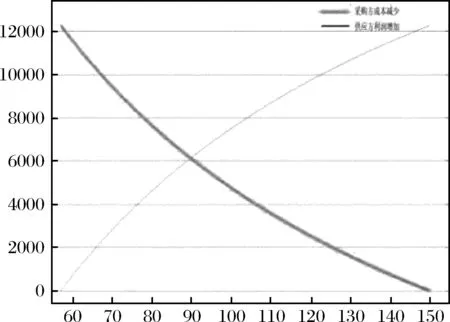
(1)v (2)b>v:否则采购方将不会参与回购契约; (3)e>v+o:保证采购方参与看跌期权契约; (4)e (5)m>w+o:否则采购方将不会进行事前的采购与储备。 传统采购储备模式下,采购方(政府)主要是通过批发价格契约从供应方处采购应急物资并进行储备,因此本文首先对基于批发价格契约的采购储备模式进行分析。批发价格契约下,采购方将从供应方处采购Qw单位的应急物资,并储备于自身储备库中,以备灾害事件发生时进行调用,采购成本为wQw,而供应方则按照采购方的采购量安排生产,生产成本为cQw。则在一个轮换周期T内: (1)当应急物资需求量为0 (2)当应急物资需求量为Qw 综上所述,采购方的成本函数为: ΠwP=wQw-vmax{Qw-x,0}+mmax{x-Qw,0} (1) 其中第一项为采购方的采购成本,第二项为剩余物资的残值,第三项为采购方的缺货成本。因此可知采购方期望成本函数为: (2) (3) 而当供应链采用集中决策时,整体供应链的生产量(采购量)为Q,则整体供应链的利润函数为: Π=vmax{Q-x,0}-cQ-mmax{x-Q,0} (4) 其中第一项为剩余物资残值,第二项为物资生产成本,第三项为缺货成本,则可知整体供应链的期望利润函数为: (5) 为进一步突出基于看跌期权契约采购储备模式的优越性,现对基于回购契约的应急物资采购储备模式进行分析。与批发价格契约相同,回购契约下,采购方将从供应方处采购Qb单位的应急物资作为自身的实物储备,采购成本为wQb,而供应方则按照采购方的采购量进行生产,生产成本为cQb。在一个轮换周期T内: (1)当应急物资需求量为0 (2)当应急物资需求量为Qb 综上所述,采购方的成本函数为: ΠbP=wQb-bmax{Qb-x,0}+mmax{x-Qb,0} (6) 其中第一项为采购方采购成本,第二项为采购方将剩余物资回售给供应方获得的收益,第三项为采购方的缺货成本。此时采购方的期望成本函数为: (7) (8) 其中式(8)中的第一项为供应方收入,第二项为供应方生产成本,第三项为供应方的回购支出,第四项为供应方的残值收益。 -(m-w)Q*+mμ (9) (10) 从式(9)和式(10)可以看出,当供应链达到协调状态时,采购方期望成本和供应方期望利润均与回购价格无关,因此在回购契约下,采购方与供应方无法通过调整回购价格来协调分配整体供应链的利润。 在一个轮换周期期初,采购方将与供应方签订看跌期权契约。在双方商定看跌期权中的权利金o与执行价格e后,采购方将根据契约参数确定采购量Qo和期权购买量qo,供应方则会根据采购方的采购量安排生产。 在一个轮换周期T的期初,采购方向供应方采购Qo单位物资作为自身实物储备的同时,还会购买qo单位的期权,支付价款wQo+oqo,而供应方将按照采购方的采购量安排生产,生产成本为cQo。在周期T内: (1)当应急物资需求量为0 (2)当应急物资需求量为Qo-qo (3)当应急物资需求量为Qo 综上所述,采购方的成本函数为: ΠoP=wQo+oqo-emin{max{Qo-x,0},qo} -vmax{Qo-qo-x,0}+mmax{x-Qo,0} (11) 其中第一项为采购方的采购成本,第二项为其看跌期权的购买成本,第三项为采购方执行看跌期权时获得的收益,第四项为采购方执行完看跌期权后,仍有剩余物资的残值收益,第五项为采购方的缺货成本。由于采购方的目标为其成本最小化,因此采购方的最优决策为: s.t.Qo≥qo,Qo>0,qo>0 (12) (13) 证明:对式(12)分别求关于Qo,qo的一阶,二阶导数得: (14) (15) (16) (17) (18) s.t.Qo-qo≥0,Qo>0,qo>0,λ≥0 (19) 即等价为: (20) 由于性质1的证明简单,在此不做详细证明。 因为随着权利金价格的增加,采购方单位物资的平均采购成本和期权购买成本也在增加,所以采购方会减少采购量和期权购买量。同理可知,采购方的采购量和期权购买量会随着执行价格的增大而增大。 从性质2中可以看出,与批发价格契约相比,看跌期权契约不仅能帮助采购方有效降低其保质期风险,而且还能提高采购方的采购量,即可有效地降低采购方的缺货风险。 性质3:当看跌期权契约的权利金o=0时,看跌期权契约与回购契约等价。 由于性质3的证明简单,在此不做详细证明。 通过性质3可以看出,回购契约其实是一种特殊的看跌期权契约,即权利金为0,执行价格为回购价格的看跌期权契约。 (21) (22) 其中式(22)的第一项为供应方收益,第二项为供应方生产成本,第三项为供应方权利金收入,第四项为采购方执行期权契约时供应方支出,第五项为供应方的残值收益。 由于已知看跌期权契约下采购方的期望成本函数及供应方的期望利润函数,因此可得看跌期权契约下,供应链达到协调时的具体条件,如命题2。 性质4:当供应链达到协调状态时,看跌期权契约中的期权契约执行价格e是权利金o的增函数。 由于性质4证明简单,在此不做详细证明。 因为采购方在期初通过支付权利金,获取让供应方按照契约中约定的执行价格回购剩余物资的权利,所以执行价格将大于权利金,并且随着权利金的增大而增大,否则采购方将不会参与到看跌期权契约中,这与之前有关研究看涨期权契约的文献中,当供应链达到协调状态时,执行价格随着权利金增大而减小的结论有所不同。 性质5:当供应链达到协调状态时,采购方的期望成本和供应方的期望利润均会随着权利金o的增大而增大。 (23) 则权利金o是采购方期望成本的增函数,即采购方期望成本随着权利金的增大而增大。 同理可知: (24) 则权利金o是供应方期望利润的增函数,即供应方期望利润随着权利金的增大而增大。 由性质5可知,当供应链达到协调状态时,随着权利金的减少,采购方期望成本也在减少,因此采购方会选择较低的权利金,而供应方期望利润会随着权利金的增大而增大,故其偏好较大的权利金,因此采购方与供应方可以通过对权利金的设定对整体供应链进行利润分配及风险共担。 与批发价格契约相比,参与看跌期权契约后,采购方期望成本的变化为: (25) 而供应方参与看跌期权契约后,其期望利润变化为: (26) 为确保采购方与供应方均能够参与期权契约,需要满足: (27) 命题3:协调状态下,当权利金的取值范围为o∈[omin,m-w)时,看跌期权契约可有效降低政府成本,并提高供应方收益,实现双方协调共赢。(其中omin=max{0,ot},ot满足ΔΠM|o=ot=0) (28) 当minΔΠM≥0时,则o≥0时,ΔΠM≥0恒成立;当minΔΠM<0时,由于maxΔΠM|o=m-w>0,因此可知存在一个临界值ot,满足ΔΠM|o=ot=0,当o≥ot时,ΔΠM≥0恒成立。因此当max{0,ot} 综上可知,当max{0,ot}≤o 通过Matlab13.0对模型进行数值模拟,可知批发价格契约和回购契约下的采购方最优采购量以及采购方与供应方的成本利润情况如表2所示。从表2可以看出,虽然回购契约下,采购方采购量及整体供应链利润均优于批发价格契约,并且可有效地降低采购方成本,但此时供应方利润却低于批发价格契约下的利润,即采购方成本的降低是建立在损害供应方利润的基础上,因此理性的供应方不会参与该回购契约中。 表2 批发价格契约和回购契约下最优采购量及双方收益对比 表3则给出了看跌期权契约下,执行价格,采购方最优决策和采购方与供应方之间的利润分配随权利金o的变化情况。o满足o∈[omin,m-w),并且按照0.1的步幅增长。如表2所示,权利金从57.1增加到149.9,执行价格从96.2 增长到199.9,采购方的最优采购量恒为4503,期权购买量从2329降低到1387。在供应链利润分配方面,采购方期望成本从212369增加到224626,供应方期望利润从62335增加到74593,而采购方期望成本的减少量从12265减少到7,供应方期望利润的增加量从9增长到12267,整体供应链的增加值为定值12274。由于可以看出,与回购契约一样,看跌期权契约下采购方最优采购量及整体供应链的利润均要优于批发价格契约,并有效地降低了采购方成本。虽然看跌期权契约下,采购方成本的降低幅度要小于回购契约,但却有效地保障了供应方利润,即采购方成本的降低并不会损害供应方的利益。由于看跌期权契约实现了双赢的结果,因此理性的采购方与供应方均将会参与其中。 表3 期权价格对采购方和供应方决策及利润分配的影响 注:表2中“采购方成本减”项目的值为-ΔΠP,“供应方利润增加”项目的值为ΔΠM 图1 采购方最优期权购买量随权利金变化曲线 图2则反映了采购方成本的减小值随着权利金的增大而减小,供应方利润的增加值随着权利金的增大而增大,这与性质5相符,由于采购方成本减小量与供应方利润增加量的和为定值,因此两者变化的绝对值相等,即当供应链处于协调状态时,期权权利金将决定采购方与供应方之间利润的分配,当权利金o较小时,采购方的期权购买量将会增加,此时采购方将风险更多的转移给了供应方,因此采购方分得了更多的利润,从而更有效的降低成本。当权利金o较大时,与上述情况相反。 图2 采购方成本减小和供应方利润增加随权利金变化曲线 针对食品医药品等一类应急物资,本文建立了基于看跌期权契约的物资采购储备模型,用以解决其在储备过程中产生的保质期风险。通过模型推导,本文证明了与批发价格契约相比,合理地设置看跌期权契约中的契约参数,可使在供应链达到协调,降低政府成本的同时,也能够提高供应方的利润,并给出了实现政府和供应方协调共赢的具体条件。此外,通过推导也证明了在看跌期权契约下,当供应链达到协调状态时,契约的执行价格,采购方期望成本和供应方期望利润均随着权利金的增大而增大,这与此前学者在看涨期权契约下得出的研究结论有所不同。最后,本文通过数值模拟的方式,显示了基于回购契约的采购储备模式虽然能很好的应对应急物资的保质期风险,降低政府成本,但会损害供应方的利益,而看跌期权契约则可以通过调整权利金,对供应链的整体利润进行合理分配,从而能够更好地保障供应方的利益,提高供应方参与的积极性,实现政府与供应方双赢的目标。3 批发价格契约下采购方决策
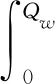
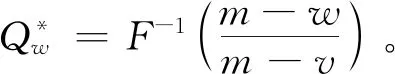


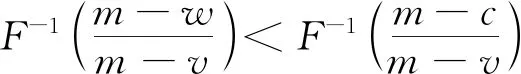
4 回购契约下采购方决策


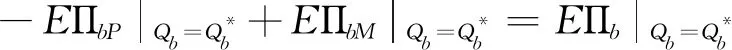
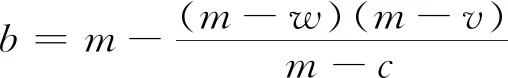
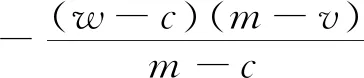
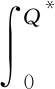
5 看跌期权契约下采购方决策
5.1 采购方与供应方的决策流程
5.2 采购方决策
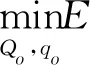


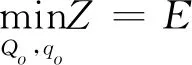
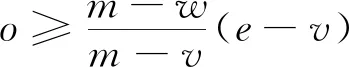
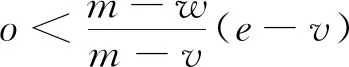
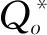

5.3 供应链协调

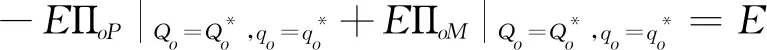
6 看跌期权契约参数的设置

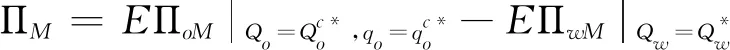

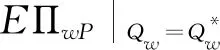
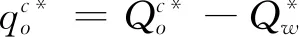



7 算例分析
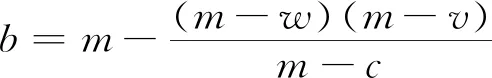



8 结语
