满意度测评中的晕轮效应分析

周洪美 ，何 训 ，高 昊

(中国人民大学 a.商学院；b.经济学院，北京 100872)

满意度测评中的晕轮效应分析

周洪美a，何 训a，高 昊b

(中国人民大学 a.商学院；b.经济学院，北京 100872)

满意度测评中，一般需要同时测量一个产品或服务的分项满意度和总体满意度。研究发现，总体满意度与分项满意度的访问顺序不同会导致总体满意度出现显著差异，造成这种现象的原因可能是晕轮效应的存在。调查发现，晕轮效应主要受到分项指标极端值以及极端值与最大绝对离差的影响。

总体满意度；分项满意度；晕轮效应

随着市场竞争的加剧以及客户导向理念的发展，客户满意度以及成为许多企业非常重视的一个方面。为了改善客户的满意度水平，首先需要了解客户满意度的现状，一般需要通过调查的方式进行客户满意度测评，通常的做法是把产品或服务按照类别分成若干个可以衡量的指标，除了让客户对这些指标分别进行评价，同时也会让客户对该公司的产品或服务的总体满意度做出一个评价，然后通过相关模型来计算得出满意度得分。

在让客户评价总体满意度时，一种做法是让用户先给出一个总体满意度的评价，然后再对各个分项进行评价，另外一种做法是让用户先对各个分项进行评价，然后再对总体满意度进行评价。两种做法中第一种的结果是客户的第一反应，而第二种结果则是对用户进行了分类指标的满意度评价提示后的一个衡量，两者的差异在很大程度上是由于满意度测评中存在晕轮效应引起的。

1 晕轮效应简介

Thorndike(1920)第一次正式提出了晕轮效应的概念，指出在对某一行为主体进行评价时，如果该主体的某一方面表现特别突出，就会对其他方面的评价产生影响，使得其他方面的表现不能被真实反映出来，这一现象就是晕轮效应。

对于晕轮效应影响的测量存在一定困难。首先很难确定真实水平，其次方法的选择存在困难，因为晕轮效应是一种主观效应。Lachman和Bass(1985)将评价对象按照总体印象分数的高低分成两组，然后采用方差分析方法检验对这两组评价对象的具体属性评价是否具有显著差异，如果存在显著差异，则说明存在晕轮效应。这种研究思路得到了业界学者的认可。

为了测量晕轮效应的影响，我们在同一次满意度调查中分别在分项满意度调查前和分项满意度调查后让客户对总体满意度分别进行评价。由于经过各个分项满意度测评的提醒作用，我们认为分析测评后的总体满意度更接近真实情况，分析测评前的总体满意度与它的差异是由晕轮效应引起的。在此，我们定义晕轮效应Ha为：

其中S1为分项测评前的总体满意度结果，S2为分项测评后的总体满意度结果。

2 数据说明和描述统计结果

该项数据来源自国内某知名物流企业的企业客户的满意度调研结果，调研时间为2009年7月，包括对国际快递业务、国内快递业务和同城快递业务的调查结果。对三种业务样本的调查结果进行同分布检验，发现三种业务的调查结果分别无明显差异，因此把三种业务的样本作为同一个整体分析，成功样本共计1387个。满意度评价采用10分制，1分最低，10分最高。

我们对S1和S2做描述统计，结果见表1。可以发现S1的平均值和标准差均高于S1。

除了总体满意度外，我们还对技术能力/安全可靠性/查询方便性等19个分项指标进行了测评。由于某一项指标的极端表现可能会产生晕轮效应，因此我们选取每个样本的19个分项指标评价结果的最大值、最小值、平均值以及距离均值的最大绝对离差值作为解释变量。其中，最大绝对误差为：

表1 总体满意度评价的描述统计结果

表2 分项评价指标的描述统计结果

表3 晕轮效应与其他因素的相关分析

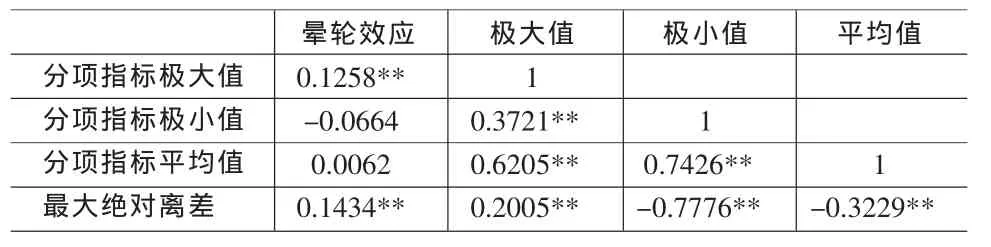
表4 晕轮效应与其他因素的相关分析（晕轮效应>0）

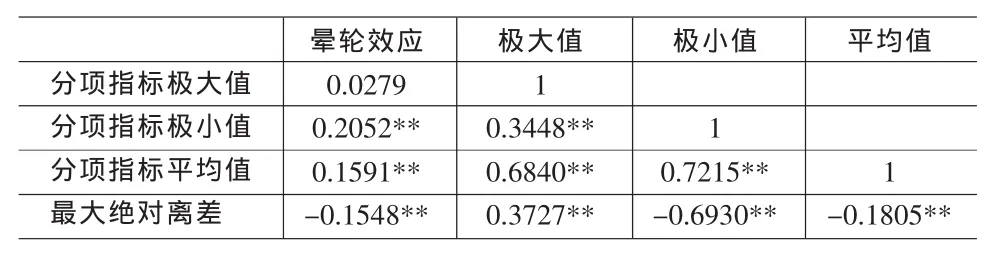
表5 晕轮效应与其他因素的相关分析（晕轮效应<0）

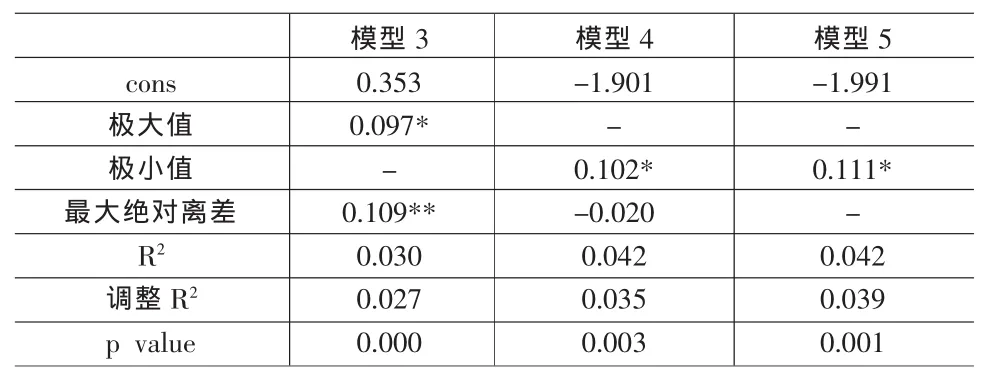
表6 晕轮效应与其他因素的回归分析结果

3 对晕轮效应的分析

对S1和S2进行等方差检验，发现S1的标准差显著大于S2，采用F检验的相伴概率为0.0025。均值T检验的结果也证明S1和S2存在显著差异，t检验的相伴概率值为0.000。因此我们认为S1和S2之间存在显著差异，而这种差异证明了晕轮效应确实存在。

将晕轮效应定义为S1与S2的差值。相关分析发现晕轮效应和分析指标极大值、平均值以及最大绝对离差均显著相关，而与极小值的相关系数不明显。这与我们的常识不符。对晕轮效应进行统计，发现晕轮效应大于0的占比远远超过小于0的占比，因此有可能极小值的效应会被淹没。因此应当对晕轮效应大于0和小于0的样本分布进行分析。

单独的分析结果表明，在晕轮效应大于0时，极大值对晕轮效应有显著相关关系，而与极小值的相关关系不显著。而当晕轮效应小于0时，结果恰恰相反，晕轮效应主要收到极小值的影响，而与极大值关系不大。

由于最大绝对离差有平均值和极值决定，对晕轮效应进行回归分析是只考虑极值和最大绝对离差（否则会具有共线性）。对晕轮效应大于0的样本进行回归分析，得到如下模型：

晕轮效应=0.353+0.097*极大值+0.109*最大绝对离差(3)

模型和系数均通过检验。极大值和最大绝对离差对晕轮效应有正的影响，但极大值的影响要小于最大绝对离差，这是由于不同样本极大值的差异较小，而其余平均值的差异程度即该指标的突出表现程度对晕轮效应的影响更大。

对晕轮效应小于0的样本进行回归分析，得到如下模型：

该模型通过检验，但最大绝对离差的系数没有通过检验。这是由于分析指标较多，使得均值主要受其他指标的影响而导致最大绝对离差对模型的解释作用不明显。

因此我们只用极小值进行回归，得到模型：

模型通过检验，而且与模型（4）相比，其调整R2还有所提高，因此模型（5）的效果更好。

如果比较模型3和模型5，发现模型5的R2和调整R2均高于模型3，即模型5的解释效果更好，这说明负的晕轮效应更明显，即如果某一个分项指标表现的比较差，很容易对总体满意度产生负面的晕轮效应，而表现的好的话正面的晕轮效应并不如负面的晕轮明显。

4 结论

在满意度调查中，分项指标对总体平均存在晕轮效应，极值的效应明显。当晕轮效应大于0时，极大值越大具有越高的正的晕轮效应，而当晕轮效应小于0时，极小值的影响更大，而且极小值越低晕轮效应越小（其绝对值越大）。

晕轮效应使得高者越高，低者越低，而且负面晕轮效应更明显。因此我们在提高服务时尽量避免某些指标出现短板，同时要有突出表现的指标。

[1]ThorndikeE L.A ConstantErrorin PsychologicalRatings[J].Journal of Applied Psychology，1920，(4).

[2]Lachmam S J.，Bass A R.A Direct Study of Halo Effect[J].Journal of Psychology，1985,119(6).

[3]风笑天.社会调查中答案顺序对调查结果的影响[J].华中师范大学学报(人文社会科学版)，2008，47(2).

(责任编辑/浩 天)

F224.9

A

1002－6487（2011）03－0173-02

周洪美（1979-），男，安徽利辛人，博士研究生，研究方向：企业管理。