巧用几何画板 开展数学实验教学

张建军1 陈唐明2

巧用几何画板 开展数学实验教学

张建军1 陈唐明2

数学实验教学是指根据教学目标,充分利用实验手段尤其是运用现代教育技术,创设问题情境,引导学生参与实践、自主探索、合作交流,从而发现问题、提出猜想进而验证猜想和创造性解决问题的一种教学方式。在教师的引导下,几何画板可以给学生创造一个实际“操作”数学图形的环境,学生可以任意拖动图形、观察图形、猜测和验证结论,在观察、探索、发现的过程中增加对各种数学问题的感性认识,形成丰富的数学图像经验背景,从而更有助于学生对数学的学习和理解。同时,几何画板还能为学生创设一个进行数学“实验”的环境,有助于学生自主探究活动的开展,促进数学课程的高效学习。本文结合教学实践,谈谈如何在教学中借助“几何画板”这一平台开展数学实验教学。

一、利用“几何画板”做数学实验—在感受数学内在美中升华学习热情

弗赖登塔尔有句名言：“没有一种数学思想,以它被发现时的那个样子发表出来。一个问题被解决以后,相应地发展成一种形式化的技巧,结果使得火热的思考变成了冰冷的美丽。”在教学中,学生往往被“冰冷美丽”的数学所吓倒,数学成了枯燥的代名词,学生对数学的学习缺少热情。利用“几何画板”的独特功能,在做数学实验过程中适时展现数学独特的内在美,让学生在感受数学美的过程中激发学习数学热情。

教学案例1：雪花曲线(Kock曲线)

利用几何画板的迭代功能作一个等边三角形,三等分每一边,然后在此等边三角形的每一边上向外部作新的等边三角形,使得新的等边三角形的两个顶点正好落在原等边三角形的三等分点上,此时形成一个六角星,然后,在所得六角星的12条边上分别重复上述步骤……如此下去所得曲线称为雪花曲线。

图1

通过上述“几何画板”操作充分展示了数学图形的美,让学生看后心旷神怡、浮想联翩。激发了学生的好奇心和内心探索未知世界的欲望,以饱满的热情投入到数学学习中。而在学生亲自实践操作中,不仅能及时巩固所学知识,还增强了学生发现问题、分析问题、解决问题的能力,同时培养了学生自主探索能力与合作交流意识。真正做到了知识与技能、方法与过程、情感态度与价值观“三维目标”的和谐统一。

二、利用“几何画板”做数学实验—在体验知识发生过程中提升思维能力

运用“几何画板”开展教学,有利于教师引导学生广泛开展面向过程学习,以达到对知识形成过程更为深刻地理解,学生能够主动参与到知识形成过程中去,体现了学生的主体作用。学生在教师的指导下,借助于几何画板进行开放性实验,通过改变问题情境,从变化中寻找规律,挖掘知识间的内在联系,并通过合理推理等手段发现结论,从而实现知识的有效建构。

教学案例2：双曲线的概念教学

现场制作：①在平面上,作线段 F1F2,度量其长度,定义为 2c；②作直线,在上取两点 A,M ,作线段 A M,度量其长度,定义为 r1；③在点M的右侧再取一点B,使,度量线段 MB 的长度,定义为2r,度量AB的长度,定义为 2a；④以线段 A M为半径,以点 F1为圆心,作圆 C1；⑤以线段 B M为半径,F2为圆心,作圆 C2,如图2所示。拖动点M在上运动,一定条件下圆 C1和C2就会产生交点(设交点记为P),P的轨迹为椭圆。

图2

此时,提出问题：⑴两圆相交的条件是什么?⑵两半径之差是多少?⑶怎样使两圆相交?⑷点P满足的几何条件是什么?⑸怎样出现双曲线的两支?⑹通过上述实验,你认为如何严格定义双曲线？

从而引导学生发现结论：平面上一个动点到两个定点的距离的差的绝对值是一个定值,且这个定值小于两定点问的距离的点的轨迹是双曲线。

上述案例提供的情境从椭圆开始,通过一系列的变换,让学生感觉到椭圆与双曲线的内在联系。从线段长度的变化引发曲线质的差异,让学生在感性认识的基础上经过思维的提炼上升到理性的高度。几何画板提供了一个实验情境,是传统的方法所无法比拟的。

三、利用“几何画板”做数学实验—在运动与变化中突破静态思维的束缚

广泛的应用性与高度的抽象性是数学的特点,也是学生产生兴趣与学习的难点所在,解决好数学的抽象性问题,是帮助学生克服难点、提高兴趣的关键。因此,利用图像帮助学生理解运用数学知识就显得非常重要。然而,学生在学习过程中接触到的书本图形都是静态的,久而久之就形成了一种潜在的静态思维,即比较擅长于用静态的角度去看待数学问题。而许多数学问题反映的是动态变化中的某些规律。常规的教学手段,往往只能处理一些静止的问题,给学生的观察、想象带来了一定的困难。而借助“几何画板”则可以得到截然不同的效果。

教学案例3：函数图像交点问题的互动研究案例

（让学生先独立思考,教师巡视。片刻后,通过实物投影展示生1的解题过程。）

师：（稍作停顿）有没有同学有不同看法？

片刻沉默之后,有学生举手,笔者示意他回答。

生2：我觉得有点问题。原方程有唯一解,对方程x2−(a−1)=0来说,应该有两种可能：无解或解亦为零。故。

师：很好！刚才生1将两函数图像有唯一公共点的问题转化为方程有唯一解的问题,将“形”的问题转化为“数”的问题,思路正确！美中不足的是考虑问题不全面,生2已经帮他解决了！

师：下面让我们再来看生1的方法二。噢,他将f (x)和 g (x)进行了求导,(未解完)请你说一下：为什么要进行求导？

生1：我想画图。

师：很好的想法！这个问题本来就是研究两个函数图像交点的问题么！画图应该是很自然的想法！老师事先已经用几何画板画好了 )(xf 和 )(xg 的图像,请大家看屏幕(如图3所示)。当 =a –0.35时 )(xf 和 )(xg 的图像只有一个交点,当a变化时,我们来看一下。（拖动点A,演示函数 )(xf 的图像随a值的变化而变化的情况）大家发现什么？（让a的值在1的附近变动,如图4所示）

图3

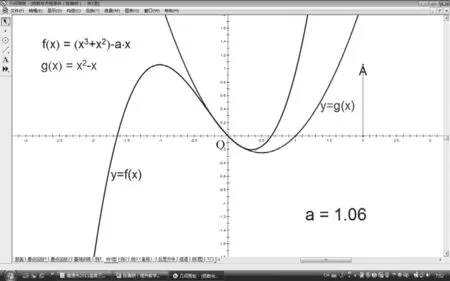
图4

师：大家试想一下,在临界位置处,用几何画板画出的图像都难以看出交点个数,更何况徒手画的示意图！华罗庚先生有句话：“数缺形时少直观,形缺数时难入微。” 直观、形象的函数图像有助我们审题分析,但细微之处亦须用“数”啊！

上述案例中,教者借助于几何画板精确画出函数图像,并通过参数的变化体现图像的交点变化情况,比学生在书本上画的静态图像更为准确、形象,有助于学生发现该题利用图像法解题的不足。

四、利用“几何画板”做数学实验—在探索知识的过程中渗透数学思想方法

在数学教学中,有目的地培养学生用数学方法去思考问题、分析问题和解决问题是十分必要的。教师可结合教材的具体内容,依托几何画板这一平台,渗透数学思想方法。

教学案例4：对数函数的图像和性质教学

图5

教师可以利用几何画板制作含参数函数的课件,如图5所示。在教学中,只要左右拖动点A时,屏幕上a的值随之改变,相应的对数函数图像也发生变化。反复拖动点A,引导学生发现、探索图像的变化规律。当时无图像出现；当 0 ＜a ＜1时,函数在区间(0,+∞)上单调减,而且a越小,图像越靠近x轴；当 a =1时,图像是一条直线,其方程为 y =1；当 a ＞1时,函数在区间(0,+∞)上单调增,而且a越大,图像越靠近x轴。通过对参数a的分类讨论,使学生理解了对数函数定义中对 a (a ＞ 0且)限制的必要性,极大地提高了教学效果,同时也为学生创造了良好的认知环境,使得教师有更多的时间有意识地渗透数学思想和方法。通过对参数a的讨论,学生学会了应用分类讨论的思想。在研究数学问题时,把数形知识结合起来,引导学生从数的方面用分析的方法进行抽象思维,从形的方面进行形象思维。数值的变化,导致形的变化,数量关系与图形如此巧妙的和谐,这里处处闪耀着数学思想的火花。

“几何画板”在数学实验中的合理运用,符合新课程理念,给学生提供了“学会学习、学会探索、学会发现”的平台,有利于增强学生学习的主动性和积极性,有利于学生思维的发展和数学思想与观念的提高。另外,从学生认知方式看,让学生学习“几何画板”成为其有力的认知工具,这无异于交给学生一把探索发现数学知识的金钥匙,是一件特别有意义的事。

[1] 陶维林.几何画板实用范例教程[M].北京：清华大学出版社,2001

[2] 张乐良.几何画板在高中数学教学中的应用[J].中国现代教育装备,2007,7

[3] 苟玉德.用几何画板把分形几何带进高中课堂[J].中学数学杂志(高中),2007,4

稿件编号：P1012067

张建军，本科，中教高级。陈唐明，本科，中教高级。

1.江苏省如东县教育局教研室。2.江苏省如东县如东高级中学。