铝合金叶轮共振振型的研究

2011-10-22刘松

失效分析与预防 2011年4期

刘松

（中航南京机电液压工程研究中心，南京 211106）

0 引言

由于振动引发的机械零件共振失效的现象，在机械失效领域常有发生，尤其是旋转类零件，如叶片、轮盘等［1-6］，更是屡见不鲜。对于机械零件共振失效的分析及改进，主要考虑振型、自振频率、振动应力和激振力的来源4个因素［7］，其中确定共振振型及相应自振频率是非常重要的。目前较为常见得出振型及自振频率的方法，主要是物理试验测量（如光弹法等）和有限元计算分析2种，但共振振型确定还是有一定难度的，工程实践过程中往往是通过对比断裂部位与各阶振型振动节线的一致性来实现。笔者应用有限元分析与一些力学理论相结合的手段，对某铝合金叶轮共振振型的确定进行了研究。

某铝合金叶轮，正常工作转速在65 000 r/min左右，设计最高转速达75 000 r/min，设计叶轮进口气体最高温度为140℃，叶轮出口气体最高温度为210℃。该叶轮为离心叶轮，材料为铝合金2A12，T4状态，叶型为直纹圆柱抛物面，采用四坐标数控铣加工。叶轮与轴采用间隙配合，靠螺母与密封环来约束其上、下安装面位移。近年来，随着产品装机使用时间的增加，该型涡轮冷却器出现多起故障。故障原因为叶轮发生共振，引起长叶片根部（靠叶轮进口处）疲劳断裂。

1 共振振型的研究

1.1 有限元模拟分析

该叶轮为整体机械加工成型，失效原因为叶轮发生共振，引起长叶片根部（靠叶轮进口处）疲劳断裂。因而可知叶片工作过程中不仅受到离心力作用，还受到气体力引起的振动应力作用。根据叶轮的受力情况和装配约束条件对叶轮进行有限元模拟仿真。有限元模拟仿真叶轮振动应力分布情况见图1。通过叶轮有限元模拟仿真结果与失效叶轮实际裂纹萌生、断裂及断口形貌（图2）对比不难发现，叶轮长叶片的根部相对振动应力水平最高，与叶轮裂纹位置一致，并且节点37 168和37 160的位置大致就是实际中叶轮共振疲劳的源区位置（其中一个长叶片）。裂纹源区及附近未发现有明显的腐蚀、夹杂等，叶片根部倒圆圆滑，可以排除材料缺陷和加工缺陷对裂纹产生的影响。

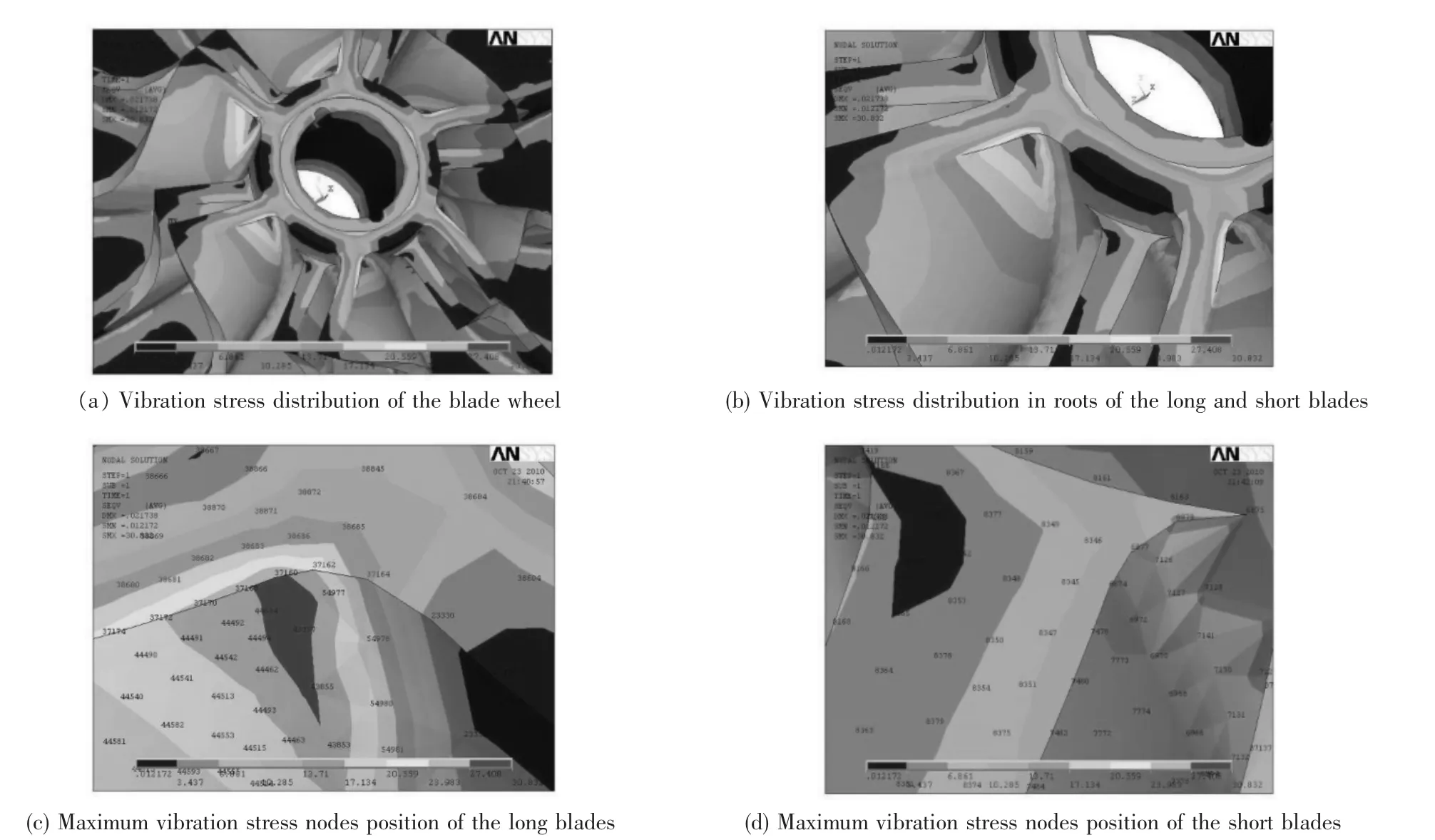
图1 有限元模拟仿真叶轮振动应力分布情况Fig.1 Vibration stress distribution of the blade wheel by finite element analysis

图2 失效叶轮裂纹及断口形貌Fig.2 Crack and fracture surface appearance of the disabled blade wheel

1.2 模态分析

影响叶轮模态分析结果的因素有弹性模量、载荷和边界约束条件，其中弹性模量和载荷主要影响自振频率，边界约束条件影响振型。弹性模量主要受温度影响，载荷主要考虑转速对其影响，边界约束条件与叶轮的实际装配有关。由于叶轮与轴的实际配合尺寸为间隙配合，靠螺母与密封环来约束其上、下安装面位移。因而设定叶轮上安装面为全约束，并约束了叶轮下安装面的径向位移。有限元模态分析的前5阶振型见图3。

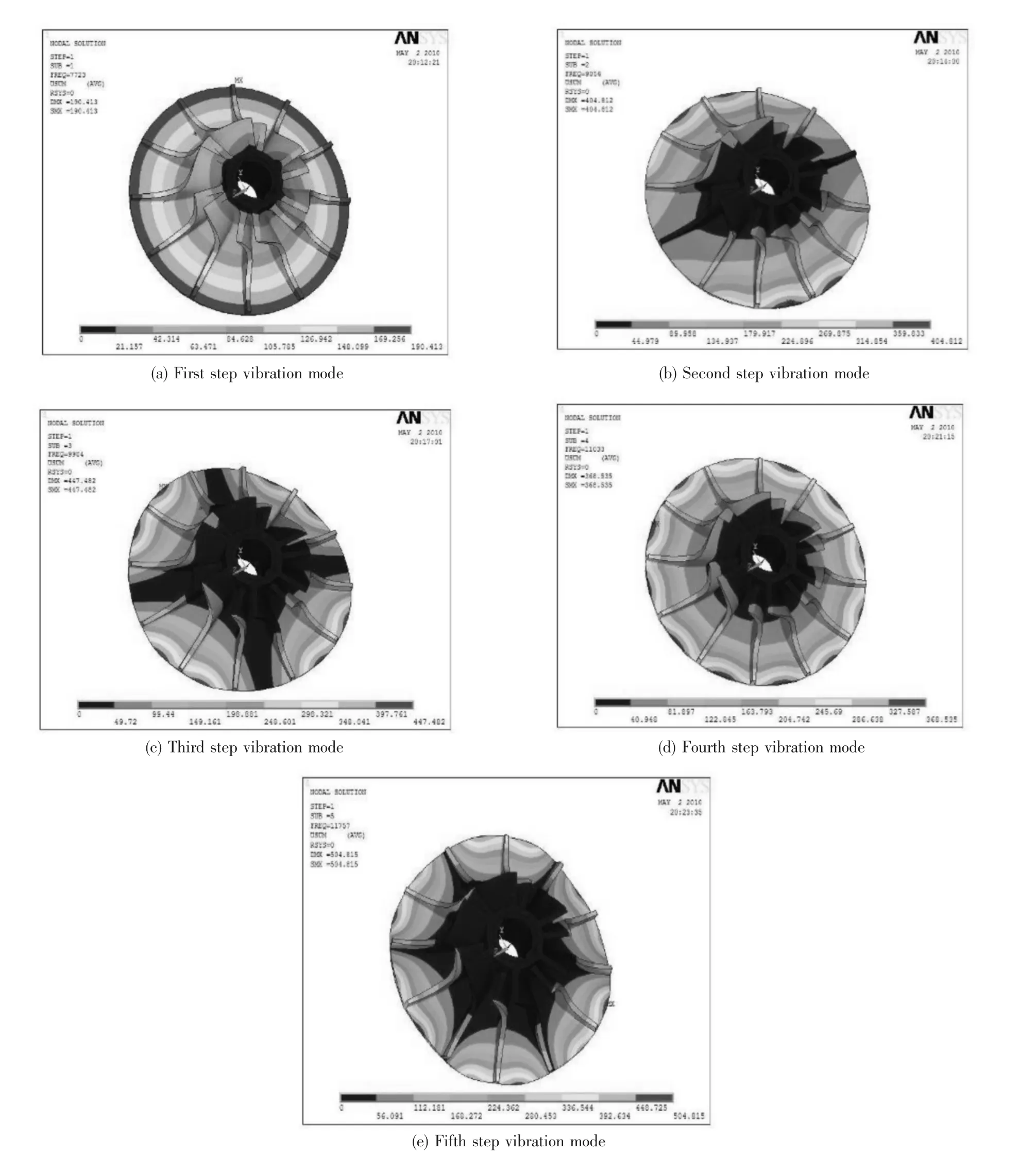
图3 叶轮的前5阶振型Fig.3 First five steps of vibration modes

1.3 共振振型的确定

笔者用节点法和Goodman力学理论相结合的方法，对共振失效振型的确定进行了研究。节点法是笔者根据有限元分析的特点总结的一套方法。由于有限元模态分析后，可以观察到叶轮在各阶振型下的振动应力，但这些应力值都只是相对值，并不是实际产生的振动应力值。

由共振失效的叶轮形貌可知，叶轮断裂和裂纹萌生的部位全部在长叶片叶背根部（叶轮进口处），短叶片从来没有发生过类似失效形貌，但长、短叶片的叶型方程是相同的（y=2.82×10-3Rx1.98）。根据这一特征，分别对长叶片裂纹萌生处的节点（源区）与短叶片相似位置的节点进行对比分析。根据图1可知，长叶片中的节点37 168和37 160大致就是实际中叶轮共振疲劳的源区，与其对应的短叶片中的节点7 478和6 874（节点37 168对应节点7 478，节点37 160对应节点6 874）。节点37 168和节点7 478在前5阶振型模态下的相对振动应力值，见表1。节点37 160节点6 874振型模态下的相对振动应力值，见表2。

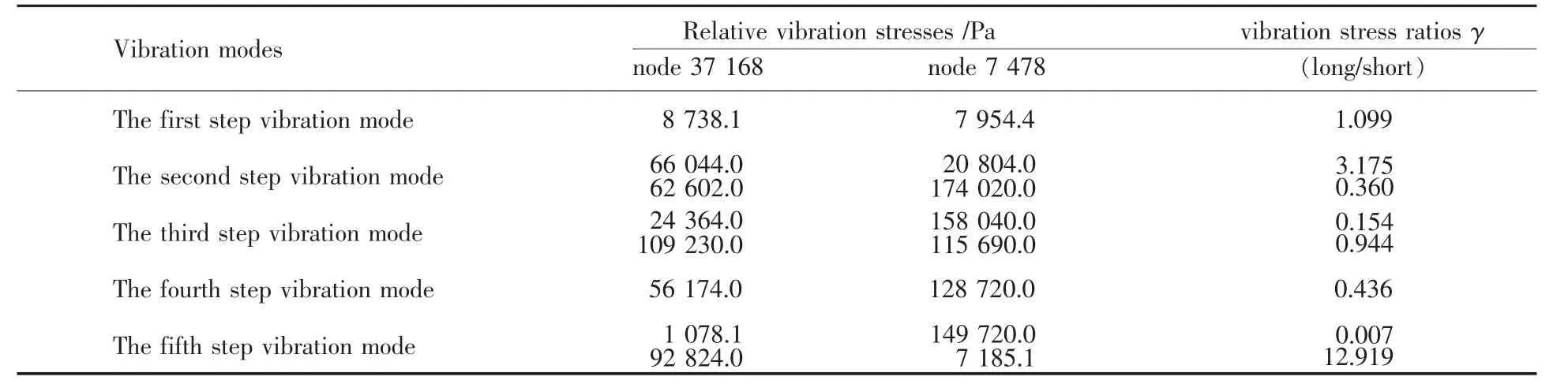
表1 节点37 168和节点7 478前5阶振型相对振动应力值Table 1 Relative stresses of node 37 168 and 7 478 in the first five steps of vibration modes

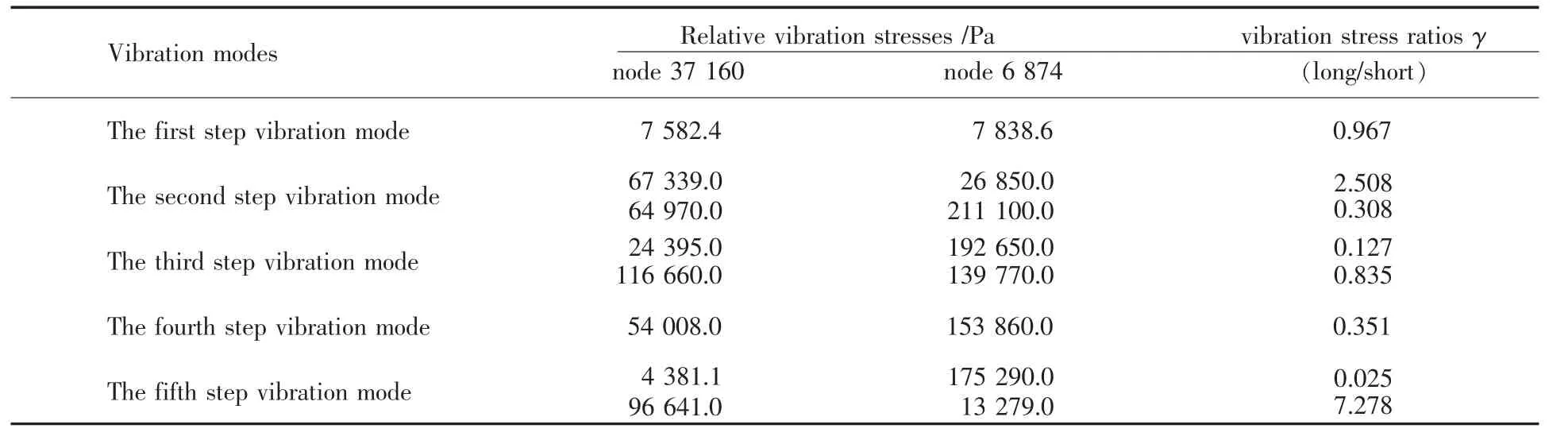
表2 节点37 160和节点6 874前5阶振型相对振动应力值Table 2 Relative stresses of node 37 160 and 6 874 in the first five steps of vibration modes

表1和表2中的2阶、3阶、5阶振型相对振动应力值分别有2组数据，这是因为2阶、3阶、5阶振型为节径型振动（全部节线都是沿径向分布），其有一定的对称性；而1阶、4阶振型为节圆型振动（全部节线都是同心圆）。

Goodman公式是讨论平均应力σm对疲劳极限σ-1影响的力学理论。工程实践应用已经证明金属材料在不同平均应力σm下，测定的疲劳极限σ-1的结果比较接近Goodman公式。Goodman公式如下

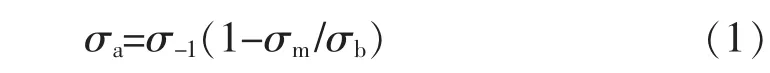
式中：σm为平均应力；σb为材料的抗拉强度；σ-1为应力比R=-1时的疲劳极限；σa为在不同平均应力下的疲劳极限。

由于振动破坏为对称循环，其应力比R=-1，但叶轮在高速旋转状态，还要受到离心力的作用。笔者应用有限元计算了节点37 160、37 168、6 874和7 478的离心力，结果见表3。

表 3 节点 37 160、37 168、6 874和7 478的离心力Table 3 Centrifugal force of node 37 160,37 168,6 874 and 7 478

叶轮工作发生共振疲劳失效时，离心力为平均应力σm，振动应力为疲劳应力幅△σ。通过文献［8］查得2A12铝合金，T4状态，25℃和 150℃下的疲劳极限σ-1分别为137 MPa和117 MPa。根据 Goodman 公式，计算出节点 37 160、37 168、6 874和7 478在离心力作用下的疲劳极限，见表4。节点37 168和7 478的Goodman曲线图见图4；节点37 160和6 874的Goodman曲线图见图5。

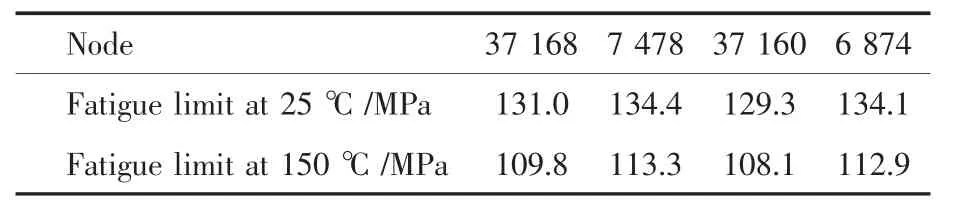
表4 节点37160、37168、6874和7478在离心力作用下的疲劳极限Table 4 Fatigue limit of node 37 160,37 168,6 874 and 7 478

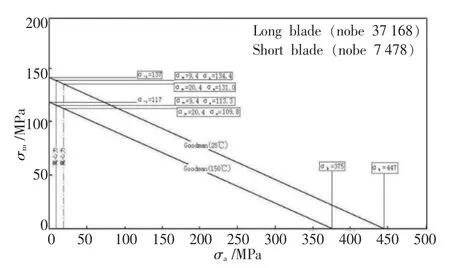
图4 节点37 168和7 478的Goodman曲线图Fig.4 Goodman curves of node 37 168 and 7 478

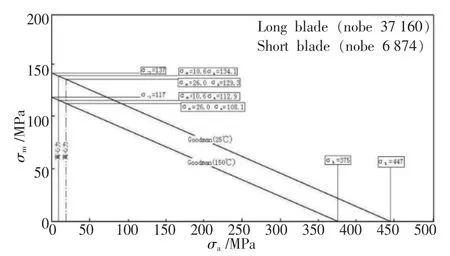
图5 节点37 160和6 874的Goodman曲线图Fig.5 Goodman curves of node 37 160 and 6 874

因为叶轮的共振疲劳失效总是发生在长叶片，而短叶片却从没有疲劳失效。因而根据疲劳断裂条件（疲劳断裂要满足疲劳应力幅值大于相应的疲劳极限）可以判定：节点37 168常温25℃时受到的振动应力大于131.0 MPa，则节点7 478常温25℃时受到的振动应力不大于134.4 MPa；节点37 168温度150℃时受到的振动应力大于109.8 MPa，则节点7 478温度150℃时受到的振动应力不大于113.3 MPa。同理，节点37 160常温25℃时受到的振动应力大于129.3 MPa，则节点6 874常温25℃时受到的振动应力不大于134.1 MPa；节点37 160温度150℃时受到的振动应力大于108.1 MPa，则节点6 874温度150℃时受到的振动应力不大于112.9 MPa。因而计算出叶轮实际工作状态发生共振疲劳失效时产生的振动应力条件，见表5。也就是说只有长、短叶片振动应力比γ满足表5的条件，叶轮才会产生共振疲劳失效。

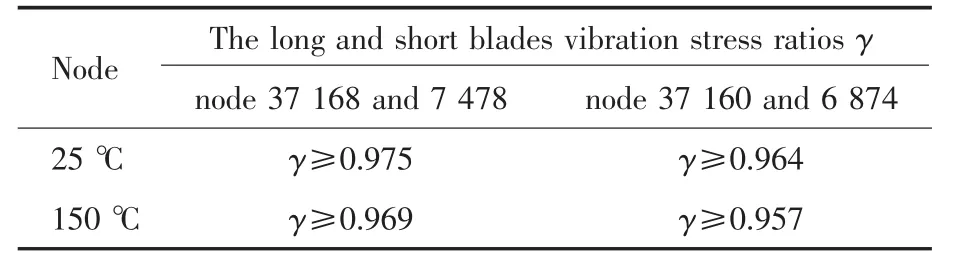
表5 叶轮共振疲劳失效时产生的振动应力条件Table 5 Vibration stress conditions of resonance fatigue fracture

根据表5可知，叶轮实际发生共振疲劳失效时，节点37 168和7 478的长、短叶片振动应力比 γ≥（0.969～0.975）；节点 37 160和 6 874的长、短叶片振动应力比γ≥（0.957～0.964）。对比表1和表2中的长、短叶片振动应力比γ可知，只有一阶振型满足条件（节点37 168和7 478的长、短叶片振动应力比γ=1.099；节点37 160和6 874的长、短叶片振动应力比γ=0.967），由此也可以确定，该叶轮共振振型为一阶振型。