富勒烯C42的密度泛函理论研究

查 林

（兴义民族师范学院，贵州 兴义 562400）

富勒烯C42的密度泛函理论研究

查 林

（兴义民族师范学院，贵州 兴义 562400）

对富勒烯C42进行了系统的密度泛函理论研究.结果显示，从能量最高的C42-01到能量最低的C42-45，分子中B55键数、五元环共用碳原子数均减少，五元环和碳原子分布更加均匀，表明这些异构体遵循五元环比邻惩罚规则.能量最低的异构体是含9个B55的C42-45.

C42；稳定性；密度泛函理论；五元环比邻惩罚原则

1 引言

1985年Kroto等[1]报道富勒烯C60后，1990年Kratschmer[2]等采用石墨棒电孤蒸发法获得克量级的C60产品，从而有力地促进了全碳分子的研究,富勒烯以及它们的内嵌、外部加成衍生物得到广泛研究[3－12].富勒烯是一类由12个五元环和不定数目的六元环组成的多面体，其中最小的富勒烯是C20.通常富勒烯的稳定性取决于五元环分离规则(IPR)，即稳定的富勒烯必须满足每一个五元环都被六元环包围.目前已经合成并分离的富勒烯都满足IPR规则.然而对于违反五元环分离规则(non-IPR)的异构体来说，通常遵循五元环比邻惩罚规则(pentagon adjacency penalty rule,PAPR),即异构体的相对能量随五元环邻接数目的增多而增大.由于融合五元环的存在，它们通常具有很高的化学活性而难于分离出来.

对于碳数小于60的小富勒烯，由于结构中存在相邻的五元环，导致其化学性质非常活泼，因而合成、分离和表征小富勒烯也就很困难.目前为止，已经合成并分离的小富勒烯仍然是廖廖无几.不过，对小富勒烯的研究可以为常见富勒烯的形成机理提供线索，因此，人们对小富勒烯的研究一直都很关注，只是研究集中在C20,C24,C28,C32,C36,C40,C44等碳数为4的倍数以及Cn(n=25～29)等小富勒烯上,对C42的研究[13]较少.为进一步了解小富勒烯的结构与稳定性之间的关系，采用密度泛函理论对富勒烯C42的所有异构体进行了几何优化，考察各个异构体的稳定性与结构之间的关系.

2 计算方法

利用富勒烯生成程序构建含五元环和六元环的C42的45种异构体，分别用C42-01～C42-45表示，由于异构体数目多，本文首先采用半经验AM1方法对所有异构体进行几何优化，再采用密度泛函理论B3LYP在6-31G*水平上对所有异构体进行了几何优化计算.全部计算采用Gaussian 03程序[14].

3 结果和讨论

计算得到异构体相对C42-45的能量⊿E、最高占据轨道（HOMO）、最低空轨道（LUMO）之间的能级差（Gap）和五元环邻接数B55列举在表1中.

从表1中可以看出,能量最低的异构体是C42-45，其次是C42-33，C42-32,能量最高的是C42-01，对称性为C2.一般而言，稳定性好的异构体具有较高的对称性，但对C42的异构体没有必然联系，C42-45的对称性为D3,⊿E在第二、三位的异构体的对称性均为C1，而⊿E最大的对称性为C2.从前线分子轨道能量差(ELUMO-EHOMO)也可以预测分子的稳定性，能量最低的C42-45的Gap最大，达到2.00 eV，不过C42-33的Gap并非排第二，而是在所有异构体中排第八位，与能量最高的C42-01相当，为1.57 eV.值得注意的是，Gap为1.89eV（排第二位）的是优化前对称性为CS的C42-19，其能量与能量最低的异构体C42-45的能量差为164.5 kJ·mol-1，应该是比较稳定的异构体.

对于富勒烯C42，根据欧拉定理[15]，无法满足独立五元环规则（Isolated pentagon rule，IPR），结构中必然存在有相邻的五元环，其各个异构体的五元环邻接数列于表1中.Campbell E.E.B[13]等预测小富勒烯Cn(20≤n≤50)，认为最稳定结构具有最少的五元环邻接数（B55）.为了考察各个异构体的相对能量与B55键数目的关系，本文绘制了⊿E与B55的关系图(图1)，能量最低的C42-45有9个B55键，能量最高的C42-01有16个B55键，B3LYP计算的⊿E与B55呈线性相关，相关系数R2=0.8643.从图1可以看出，随着B55数目的增加，异构体的相对能量上升，稳定性降低，即这些异构体满足五元环比邻惩罚规则（pentagon adjacency penalty rule,PAPR[16,17]）.

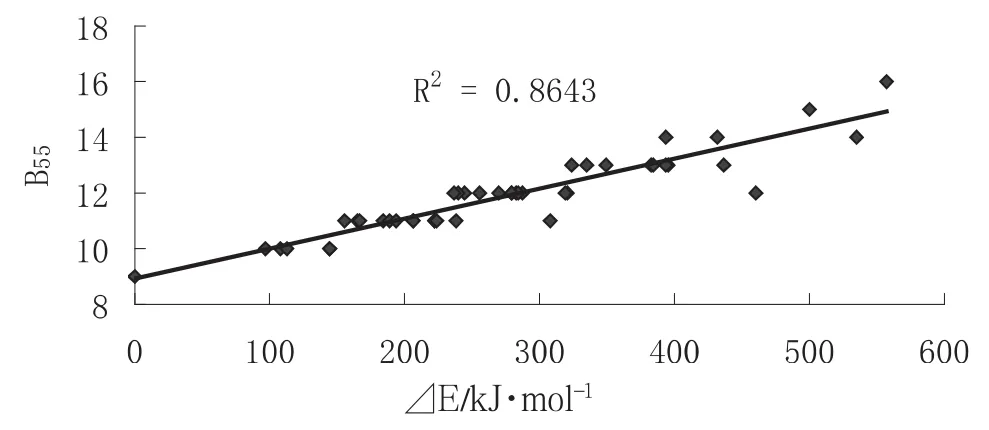
图1 ⊿E与B55的关系图

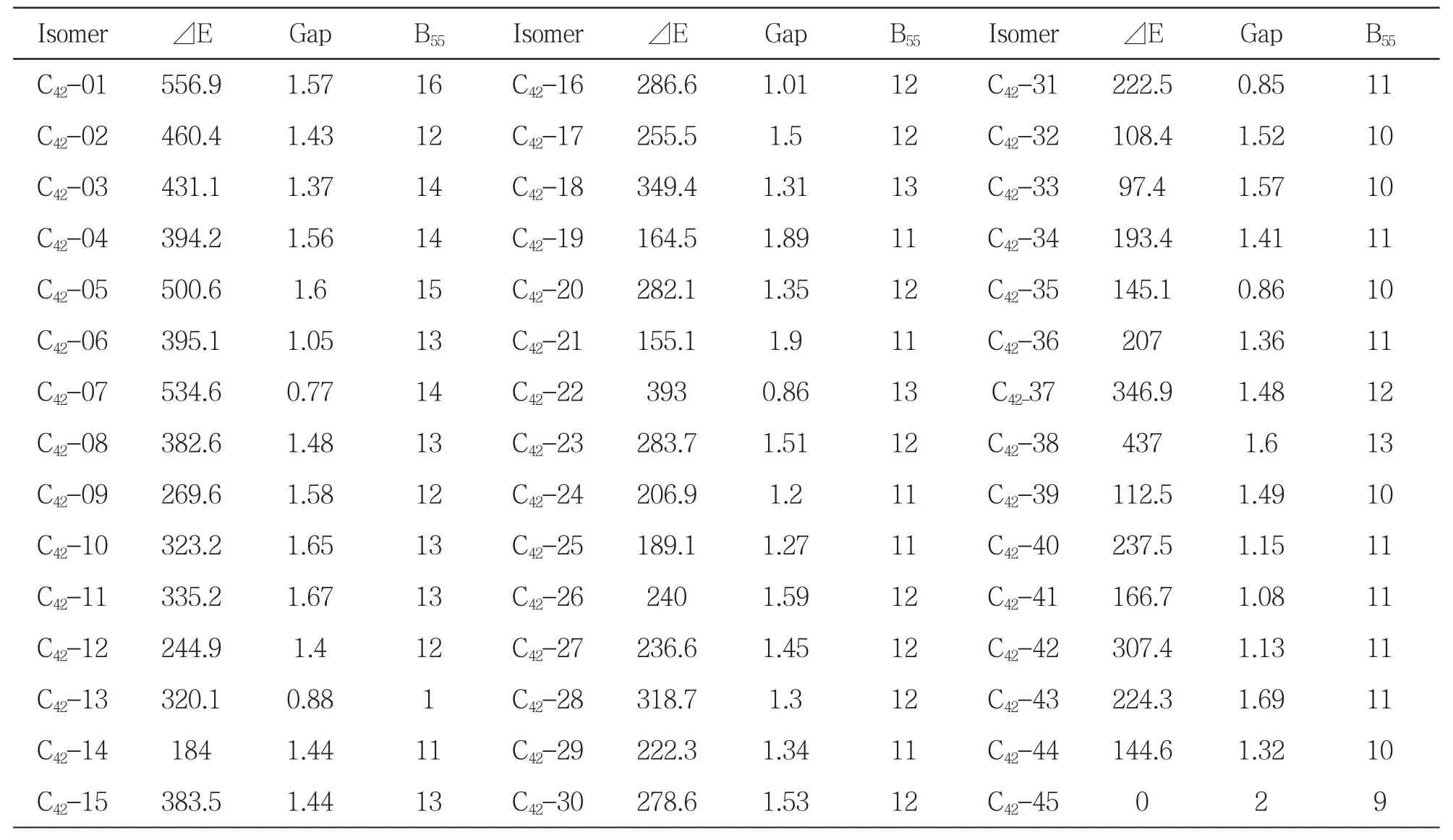
表1 C42异构体的相对能量（⊿E/kJ·mol-1）、HOMU-LUMO 能隙（Gap/eV）和五元环邻接数（B55）

为了理解这些异构体的稳定性与几何构型的关系，分别计算了通过B3LYP/6-31G*优化的各个异构体的碳原子的锥化角PA(PA=θσπ-90°，式中θσπ为sp2杂化碳原子的p轨道与相邻三个碳-碳σ键之间的角度)，将各异构体的42个碳原子锥化角的平均值PA、最大值PAMAX、最大值与最小值之差⊿PA以及标准偏差s绘制折线图于图2.

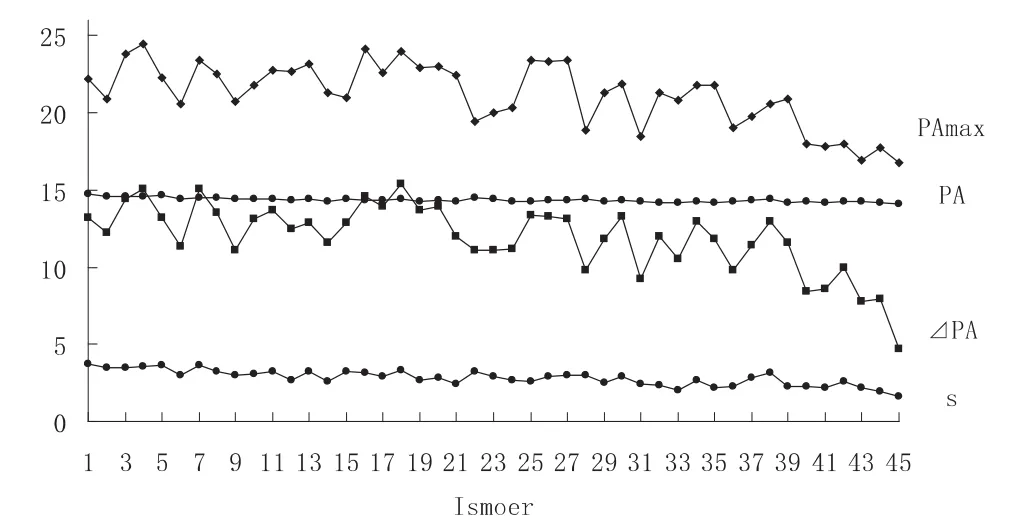
图2 C42异构体的锥化角

结果显示，各C42异构体的平均锥化角在14.11°～14.76°之间，相差无几.能量最低的C42-45各碳原子锥化角的平均值为14.11°，最大值PAMAX为16.8°，最大值与最小值之差为4.71°,平均程度可以用标准偏差s来判断，其s=1.58，无论锥化角的平均值、最大值、极差还是标准偏差，均是所有异构体中最小的，说明分子结构中碳原子的锥化角分布比较平均，碳笼没有锥化程度特别大的原子，可以预测其为C42的最稳定结构，根据表1和图2的数据绘制了相对能量与碳原子锥化角标准偏差的关系图（图3），表明随着能量的增大，标准偏差随之增大，呈线性相关，相关系数为0.8247，进一步表明，能量较低的异构体的结构中的碳原子具有较好的分布性.

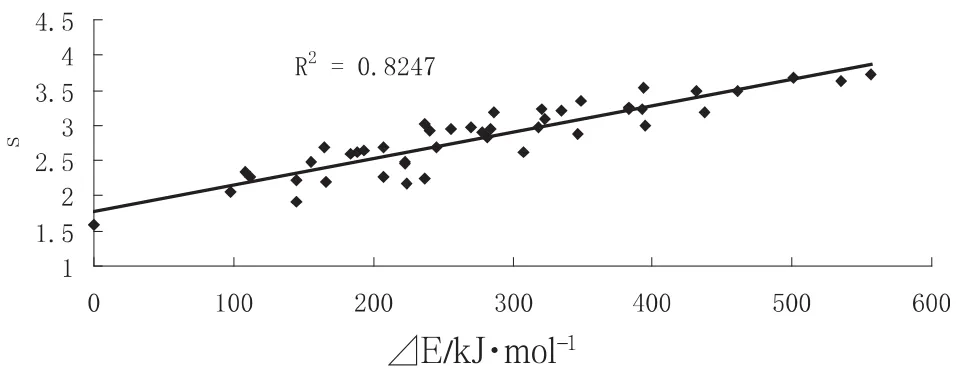
图3 ⊿E和s的关系图

从结构上看，C42-45（图4-a）分子中的五元环分布颇为特殊，存在3组4个五元环相连的结构，B55键仅有9个，没有出现3个五元环共用的碳原子.C42-41～44均没有出现3个五元环共用的碳原子,但他们的能量差均没有排在前三.能量仅次于C42-45的C42-32(图4-b)和C42-33(图4c)的五元环分布相似，均存在1个五元环共用的碳原子（C-12），1组5个五元环和一组3个五元环依次相连.而能量差排第五的C42-21(图4-d)（⊿E=155.1kJ·mol-1）存在一组4个五元环共用2个碳原子的结构，而能量最高的C42-01(图4-e)却存在2组5个五元环共用3个碳原子的结构.说明3个五元环共用的碳原子对能量的影响需要综合考虑其他五元环的分布情况，一般来说，五元环分布越平均，碳原子分布越均匀，结构越稳定.此外，五元环共用碳原子突出于碳笼，其锥化角在该异构体的42个碳原子中均为最大，他们应该具有较高的反应活性.

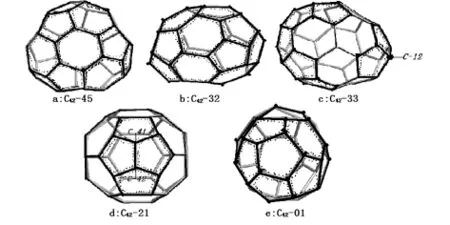
图4 C42的部分异构体的结构

4 结论

对富勒烯C42进行了系统的密度泛函理论研究.结果显示，能量最低的异构体是C42-45.从能量最高的C42-01到能量最低的C42-45，分子中B55键数、C10分子碎片数均减少，五元环和碳原子分布更加均匀，表明这些异构体遵循五元环比邻惩罚规则.

〔1〕Kroto H W，Heath J R,O'Brien S C,et al.C60:Buckminsterfullerene[J].Nature,1985,318.

〔2〕Kratchmer W,Lamb D L,Fostiropoulos K,et al.Solid C60:a new form of carbon[J].Nature,1990,347.

〔3〕Gan Lihua,An Jie,Pan Fusheng,et al.Geometrical and Electronic Rules in Fullerene-based Compounds [J].J Chem.Asian，2011,in press.

〔4〕甘利华.富勒烯结构Si60的从头算研究[J].高等学校化学学报，2006（6）.

〔5〕An Jie,Gan Lihua,Zhao Jianqiang，et al.Aglobal search for the lowest energy isomer of C26[J].J Chem.Phys，2010，132.

〔6〕张秀梅，王利光，郁鼎文，等.C20富勒烯分子及异构体的密度泛函方法研究[J].微纳电子技术,2008,45(8).

〔7〕霍新霞，王利光，郁鼎文，等.C48异构分子稳定性的密度泛函方法理论研究[J].黑龙江大学自然科学学报,2008,25(2).

〔8〕阿布力克木·克热木.C36X（X=O,NH,S）各种可能异构体的芳香性研究[J].高等学校化学学报,2006,27(3).

〔9〕王东来，焦志峰，沈洪涛，等.C32衍生物C32X2(X=H,F,Cl,Br)的理论研究[J].东北大学学报(自然科学版),2008,29(9).

〔10〕许秀芳，尚贞锋，李瑞芳，等.富勒烯衍生物 C50X(X=SiH2,PH,S)的结构及稳定性的理论研究[J].高等学校化学学报,2008,29(12).

〔11〕Albertazzi E，Domene C，Fowler P W,et al.Pentagon adjacency as a determinant of fullerene stability[J].Phys Chem.Chem.Phys,1999,1.

〔12〕刘桂霞，张红星，孙家锺，等.C40异构体的结构和稳定性的理论研究[J].高等学校化学学报，2003（1）.

〔13〕Campbell E E B，Fowler P W，Mitchell D，et al.Increasing cost of pentagon adjacency for larger fullerenes[J].Chemical Physics Letters，1996，250.

〔14〕Frisch M J，Trucks G W，Schlegel H B，et al.GAUSSIAN03，Revision B.03，Gaussian，Gaussian，Inc. Pittsburgh PA，2003.

〔15〕Balaban A T.From Chemical Topology to 3D Geometry[J].Acc Chem.Res.2000,33.

〔16〕Gan Lihua，Zhao Jiangqiang，Hui Qun. Nonclsssical fullerenes with a heptagon violating the pentagon adjacency penalty rule[J].J.Comput.Chem.，2010，31.

〔17〕Haddon R C,Scott L T. л-Orbital conjugation and rehybridization in bridged annulenesand deformed molecules in general：л-orbital axis vector analysis[J].Pure Appl Chem.，1986，58.

O641.12

A

1673-260X（2011）08-0027-03