具有p- Laplace算子的积分微分方程积分边值问题正解的存在性

王平友, 贾 梅, 窦丽霞, 金京福

(上海理工大学理学院,上海 200093)

具有p- Laplace算子的积分微分方程积分边值问题正解的存在性

王平友, 贾 梅, 窦丽霞, 金京福

(上海理工大学理学院,上海 200093)

研究了带有p- Laplace算子的微分积分方程积分边值问题正解的存在性,利用范数形式的锥拉伸与锥压缩不动点定理,得到了边值问题至少存在一个正解的结论.

积分边值问题;不动点定理;正解;锥

1 问题的提出

由于边值问题具有广泛的应用背景,因此已被深入的研究[1],尤其对于边值问题

其中,α,γ,β,δ≥0,并且αγ+αδ+βγ＞0,f∈C([0,1]×[0,+∞),[0,+∞))正解的存在性,许多作者对其做了大量的工作,并且获得了上述边值问题有解、一定为正解等结果[1-5].对于具p- Laplace算子的边值问题正解存在性的研究,也得到了许多有意义的结果[6-11].

但是,如果边界条件中涉及的点多于两个,如四点边值问题

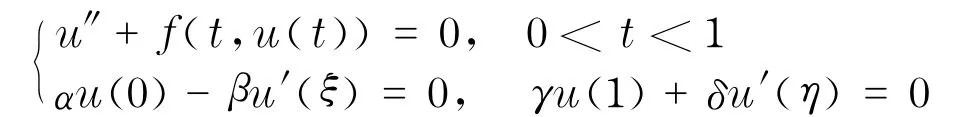
其中,0＜ξ,η＜1,并且αγ+αδ+βγ＞0,f∈C([0,1]×[0,+∞),[0,+∞)),由于其边界条件的复杂性,即使得到其解存在,也不能保证其解一定为正解[6].

文献[6]研究了边值问题

其中,φp(s)=|s|p-2s,p＞1,α,β＞0,0＜ξ＜η＜1,利用范数形式的锥拉伸与锥压缩定理,得到了边值问题至少存在一个正解、多个正解的结论.

文献[7]研究了边值问题

其中,φp(s)=|s|p-2s,p＞1,α＞0,0＜ξ＜η＜1,ξ+η=1,λ＞0,利用不动点指数理论,Leray -Schauder度结合上下解方法,得到了边值问题多个对称正解的存在和不存在的充分条件.

本文进一步讨论具p- Laplace算子的微分积分方程边值问题

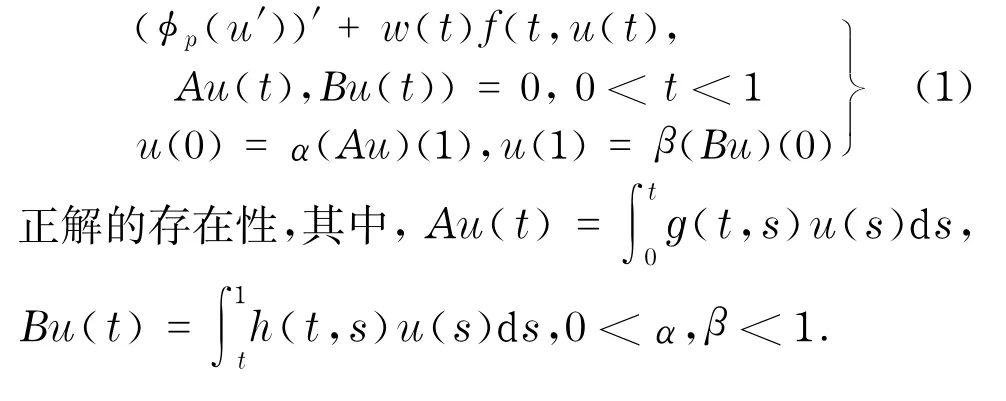
2 预备知识

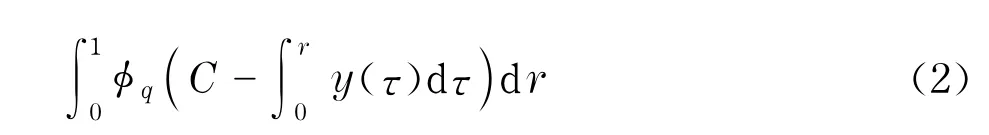
考虑边值问题

引理4设(H1)成立,则边值问题(3)的解u具有以下性质:

a.u是严格凹函数;

b.u(t)≥0,t∈[0,1];

证明假设u是边值问题(3)的解.

a.由于(φp(u′))′=-y(t)≤0,且y在(0,1)的任意子区间上不恒等于零,则φp(u′)是严格单调减函数,从而u′(t)也是严格减函数,故u(t)在0≤t≤1上是严格凹函数.

b.由a可得,对任意t∈[0,1],有u(t)≥min{u(0),u(1)}.不失一般性,可设u(0)=min{u(0),u(1)},则

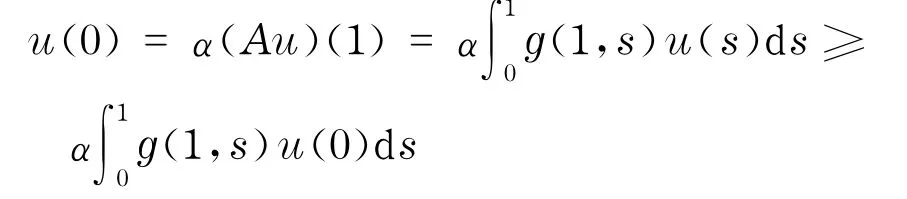
与文献[6]类似,可证引理6成立.

引理6T:K→K为全连续算子.

3 主要结果

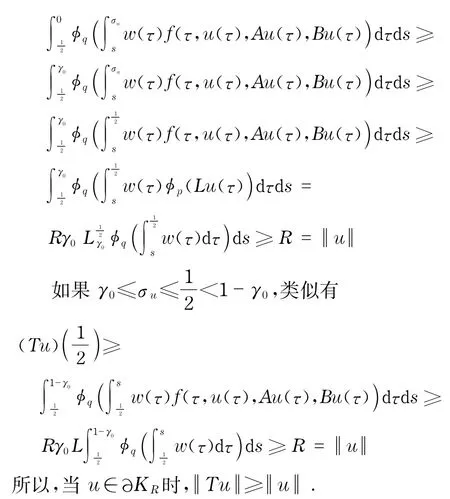
由引理7得算子T在K-RK r至少存在一个不动点u,由于u是边值问题(1)的解当且仅当u是T的不动点,故边值问题(1)至少存在一个正解u,且r≤u≤R.

定理2设(H1)和(H2)成立,且存在常数0＜ε＜1,使得下面假设成立.

由引理7得算子T在K-RK r至少存在一个不动点u,由于u是边值问题(1)的解当且仅当u是T的不动点,故边值问题(1)至少存在一个正解u,且r≤u≤R.

[1] 葛渭高.非线性常微分方程边值问题[M].北京:科学出版社,2007.

[2] GE Wei-gao,REN Jing-li.New existence theorem positive solutions for the Sturm-Liouville boundary-value problem[J].Appl Math Comput,2004,148:631-644.

[3] WEBB J R L.Positive solutions of some three point boundary-value problem via fixed point index theory[J].Nonlinear Analysis,2001,47:4319-4332.

[4] FENGHan-ying,GE Wei-gao.Multiple position for m-point boundary-value problems with aone-dimensionalp- Laplacian[J].Nonlinear Analysis,2008,68:2269-2279.

[5] MA Ru-yun,REN Li-shun.Positive solutions for nonlinear m-point boundary value problems of Dirichlet type via fixed-point index theory[J].Applied Mathematics Letters,2003,99:863-869.

[6] LIAN Hai-rong,GE Wei-gao.Positive solutions for a four-point boundary value problem with thep- Laplacian[J].Nonlinear Analysis,2008,68:3493-3503.

[7] JI De-hong,GE Wei-gao.The existence of sysmetric positive solutions for Sturm-Liouville like four-point boundary value problem with ap- Laplacian operator[J].Applied Mathematics and Computation,2007,189:1087-1098.

[8] LI Xiang-feng.Multiple positive solutions for some four-point boundary value problems withp- Laplacian[J].Applied Mathematics and Computation,2008,202:413-426.

[9] BAI Chuan-zhi,FANG Jin-xuan.Existence of multiple positive solutions for nonlinearm-point boundary value problems[J].Applied Mathematics and Computation,2003,140:297-305.

[10] WANG You-yu,HOU Cheng-min.Existence of multiple positive solutions for one-dimensionalp- Laplacian[J].J Math Anal Appl,2006,315:144-153.

[11] SU Wei-hua,WEI Zhong-li,WANG Bao-he.The existence of positive solutions for a nonlinear four-point singular boundary value problem with ap- Laplacian operator[J].Nonlinear Analysis,2007,66:2204-2217.

[12] 郭大钧,孙经先,刘兆理.非线性常微分方程泛函方法[M].2版.济南:山东科学技术出版社,2006.

Existence of positive solutions of integral boundary value problems for nonlinear integro-differential equations withp- Laplacian

WANGPing-you, JIA Mei, DOULi-xia, JINJing-fu
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

The existence of positive solution of integral boundary value problems for nonlinear integro-differential equations with the one-dimensionalp- Laplacian was studied.By using the expansion and compression fixed point theorem of norm in cone,the existence of at least one positive solution for this kind of integral boundary value problems was concluded.

integral boundary value problem;fixed point theorem;positive solutions;cone

O 175.8

A

1007-6735(2011)04-0391-06

2011-01-14

上海市教育委员会科研创新基金重点资助项目(10ZZ93)

王平友(1981-),男,硕士研究生.研究方向:应用微分方程.E-mail:wpingy2008@163.com贾 梅(联系人),女,副教授.研究方向:应用微分方程.E-mail:jiamei_usst@163.com