基于再度感染的SIS传播模型研究
2011-10-10朱晓军
朱晓军, 张 宁
(上海理工大学管理学院,上海 200093)
基于再度感染的SIS传播模型研究
朱晓军, 张 宁
(上海理工大学管理学院,上海 200093)
提出了复杂网络上一种基于再度感染的SIS传播模型.在具有树状分支结构的网络中,针对某个染病节点,在考虑其感染子节点的同时,也考查其再次感染祖先节点的情况.分别在小世界网络和无标度网络上进行仿真分析,结果表明,对于小世界网络,基于再度感染的SIS传播模型的稳态感染密度比传统的SIS传播模型的要大,而且感染周期越短,稳态感染密度越大;而对于无标度网络,虽然基于再度感染的SIS传播模型的稳态感染密度也比传统的SIS传播模型的要大,但是,感染周期对于稳态感染密度的影响微乎其微,甚至可以忽略.
复杂网络;疾病传播;再度感染;祖先节点
根据经典的疾病传播理论,疾病之所以能够在人群中传播,是因为感染个体将疾病传播给了与其存在接触的其他个体.目前研究中所用的两类特别重要的传播模型是SIR(susceptible-infected-recov-ered)和 SIS(susceptible-infected-susceptible)模型[1-2].在SIR模型中,单个个体被划分为3种类型.第一类是易感人群(S),这类人群不会感染其他的个体,但是,有可能被感染;第二类是染病人群(I),这类人群已经患病,具有传染性;第三类是移除人群或者康复人群(R),这类人群是被治愈获得免疫能力的个体或者死亡的个体,他们不再具有传染性,也不会被再次感染.
近年来,科研工作者已经研究了许多种模型,从数学形式上描述疾病传播的过程,与此同时,各种免疫策略也相继被提出来应对不同的疾病传播.Pastor-Satorras和Vespignani等用平均场的理论[3-4]研究了小世界网络和无标度网络上的SIS模型,得到这两种网络上疾病传播的阈值.Boguñá和Pastor-Satorras等[5]考察了关联网络(correlated networks)上SIS模型的传播阈值.
SIS模型与SIR模型较类似,不同的是在SIS模型中,染病人群一旦被治愈康复就立刻变成易感人群,从而使得网络中存在这样一种情况,单个易感个体可能多次再度被染病节点所感染[6].
1 基于再度感染的SIS传播模型
疾病传播研究的一个基础性问题是:一类疾病是在人群中普遍传播成为流行病,还是逐渐消亡稳定为地方病状态.大量的研究表明,解答此问题的关键在于传播率和康复率的取值大小,还有个体之间接触(连接)的方式(属性).对于SIR模型,有关传播阈值的研究已经很透彻;而对于SIS模型,关于传播阈值的分析还需考虑同一个节点多次被感染的情形,这也是本文研究的重点.
首先,将SIS和SIR传播模型的定义更加细化一点:初始时刻,除了随机选取的一个染病节点外,网络中的其他N-1个节点都是易感染类型的.每个时间步,感染节点以概率β将疾病感染给其邻接节点.节点一旦被感染后,保持感染状态达τ时间步之久,之后以概率γ或者变成康复状态(SIR)或者变成易感状态(SIS),定义有效传播率λ=β/γ,不失一般性,可令γ=1.
其次,网络中的渗流理论[7-8]指出,网络中的边会逐渐被移除直到网络中剩余节点个数所占初始节点个数的比例为p′时为止,这时存在一个渗流阈值p′c,当p′>p′c时,一个巨集团会跨越整个网络;当p′<p′c时,网络由孤立的小集团组成.疾病传播的过程可以看成是渗流过程的相反过程[9],亦即疾病传播开始于一个给定的节点,之后不断以概率在这个增长网络中添加连边.这时,疾病在网络传播的关键感染率就等同于渗流过程中出现巨集团时的渗流阈值.为了研究方便,定义一个节点感染其邻接节点的概率为p,注意这里的p不同于上面提到的β,这是因为在τ时间步内,只要染病节点还处于感染状态,它就有可能一直感染其邻接节点.因而,得到p的数学表达式为[10]

定义n i为染病节点i所感染节点的平均数量,如果n i>1,那么疾病会一直传播下去,直到达到稳定状态.在SIR模型中,只需考虑子节点(descendants)被感染的情况;而在SIS模型中,在考虑子节点被感染的同时,也需考查祖先节点(ancestors)再次被感染的可能.如图1所示,节点b1一旦被感染后,不仅能够将疾病传染给它的子节点c1,c2,…,c k-1,而且可能会传染给其祖先节点i.

图1 树状结构中基于再度感染的传播示意图Fig.1 Epidemic spreading based on reinfection in the network that has a tree like sturcture
根据图论知识,一个节点度为k(入度为1,出度为k-1)的概率为kp(k)/
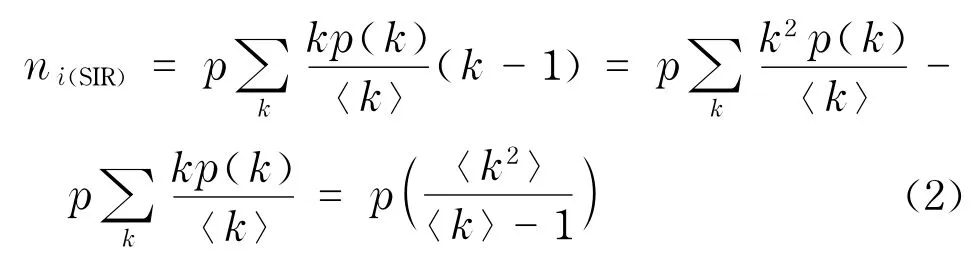
根据式(1)和式(2),由临界条件n i(SIR)=1,可得传播阈值为
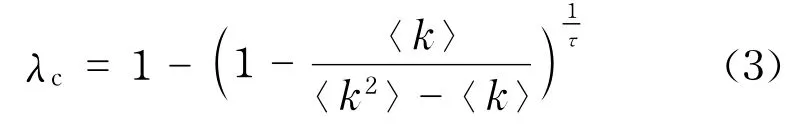
对于SIS模型,在计算n i的过程中还需考虑节点再次被感染的情况,如图1所示.但是,节点b1再度感染其祖先节点i的概率与感染其子节点c1,c2,…,c k-1的概率是不一样的.这是因为相对于子节点,节点i处于易感状态的时间是不同的.两方面的因素造成了这种结果:首先,节点i在感染节点b1之前必须是处于感染状态的,b1也必须在节点i康复后再变成易感状态才能再次感染节点i(时间因素);其次,除了节点b1,节点i的其他子节点b2,…,b k-1也可能在b1之前再次感染节点i(兄弟节点因素).
现计算SIS模型中,节点b1再次感染节点i的概率π(简称再度感染率).为了讨论方便,只考虑上面提到的第一种因素,忽略第二种因素.假定疾病的感染周期为τ时间步,节点i在感染节点b1之前有s时间步处于感染状态,那么节点i在感染节点b1之后就有τ-s时间步处于感染状态,从而节点b1就有τ-(τ-s)=s时间步反过来再次感染节点i.根据上述思想,得到再度感染率为

式中,(1-β)s-1β/(1-(1-β)τ)表示在时间步s时刻节点i感染节点b1的概率,并假设节点b1完全被感染;1-(1-β)s表示节点b1在s时间步内感染节点i的概率.
结合式(2)和式(4),不难得出基于再度感染的SIS模型中节点i所感染节点的平均数量为

根据式(1)和式(5),由临界条件n i(SIS)=1,可得传播阈值为

不难看出,相对于传统的SIS模型,基于再度感染的SIS模型中的传播阈值不仅与网络的平均度有关,还与疾病的传播率β和疾病的感染周期τ有关.
所以,在SIS模型中总的被感染节点数量可以表示为
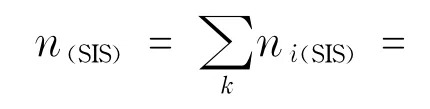
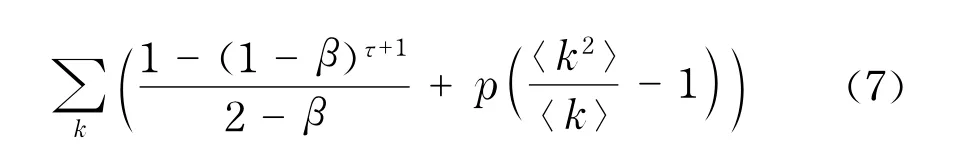
2 算法设计
根据上述理论分析的结果,设计出如下算法:
a.输入网络的邻接矩阵.邻接矩阵是一个对称的N阶方阵,N表示网络中节点的总个数.由于邻接矩阵一般是稀疏矩阵,本文使用sparse函数压缩矩阵的存储空间.
b.设置传播过程中的参数.定义传播率为p,康复率为γ,疾病的感染周期为τ时间步,程序运行时间为T.
c.设定网络中节点的状态.假设网络中全部节点的初始状态都是易感染的.用一个N维行向量node_state=1+zeros(1,N)来表示每个节点的状态.分量值若为1,则表示该节点为易感状态;分量值若为2,则表示该节点为染病状态.所以,在网络中统计染病节点密度时只需统计分量值为2的节点个数就可以了.
d.采用去尾法,随机地从N个节点中选取一个作为染病节点,这个节点的状态值从1变成2.
e.第1时间步的节点传染模拟.如果node_state(1)≠2,则跳过节点1,再分析节点2;如果node_state(1)=2,则节点1为染病节点,查找邻接矩阵中第1行值为1的所有元素所在列,即为节点1的邻接节点;若邻接节点的状态为1,则以概率p被感染,否则保持原状态,同时将被感染的邻接节点状态值标记为4,其目的是为了避免在该时间步将疾病传染给其他易感节点.对节点1的所有邻接节点重复上述步骤.对网络中的所有节点进行上述操作.
f.第1时间步的节点康复模拟.如果node_state(1)≠2,则跳过节点1再分析节点2;如果node_state(1)=2,则节点1以概率γ自动康复并迅速变成易感状态,同时将康复的节点状态标记为3.
g.第1时间步的节点状态重新标记.状态值若为4则变成2,状态值若为3则变成1.
h.重复步骤e-g,直到τ时间步.
i.第τ+1时间步的节点传染模拟.从此时间步开始需考虑再度感染的情况.此时网络中所有易感节点数目为:第1时间步状态值为1的感染节点(此刻已变为易感节点)个数加上第τ时间步统计出的易感节点个数.前者以概率π被感染,后者以概率p被感染.
j.第τ+1时间步的节点康复模拟.同步骤f.
k.第τ+1时间步的节点状态重新标记.同步骤g.
l.重复步骤i-k,直到T时间步,程序运行结束.
3 仿真分析
根据本文所提算法,使用计算机模拟疾病的传播过程,通过仿真得到的结果来分析上述方法的合理性.为了使程序简单易懂,使用Matlab7.5编写基于再度感染的SIS模型的代码.分别在WS小世界网络和BA无标度网络上仿真疾病传播的过程.取网络节点数N=10 000,WS网络中平均度
图2描述了小世界网络上感染密度ρ随着疾病感染周期τ的变化而变化的过程.从上到下3条曲线分别时在τ=2,6,10是的情形,最下方1条曲线是传统的SIS模型模拟出的结果.不难看出,疾病在基于再度感染的SIS模型中传播所达到的稳态感染密度要比在传统的SIS模型中的大,而且感染周期越短,稳态感染密度越大.

图2 小世界网络上感染周期τ对感染密度p的影响示意图Fig.2 Relation between stationary infected density p and infection lifetimeτin small world network
图3反映了无标度网络上感染密度ρ随着疾病感染周期τ的变化而变化的过程.从上到下3条曲线分别是τ=2,6,10时的情形,最下方1条曲线是传统的SIS模型模拟出的结果.从图3中可知,疾病在基于再度感染的SIS模型中传播所达到的稳态感染密度要比在传统的SIS模型中的大,但是,感染周期对于稳态感染密度的影响微乎其微,甚至可以忽略.
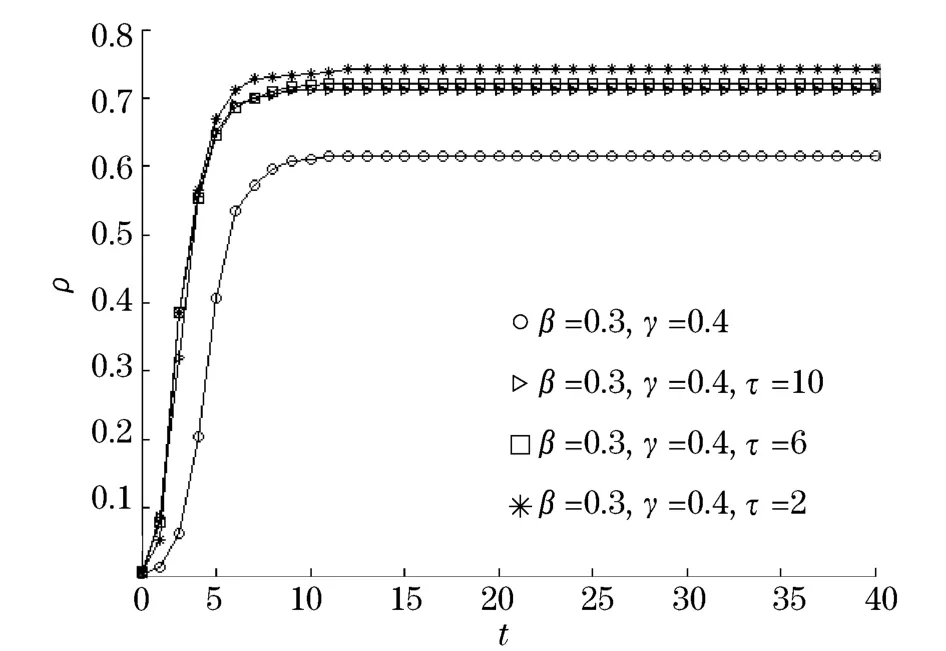
图3 无标度网络上感染周期τ对感染密度p的影响示意图Fig.3 Relation between stationary infected density p and infection lifetimeτin scale-free network
比较图2和图3可以得知,相对于小世界网络,疾病在无标度网络上传播的速度较快,也就是达到稳态感染密度所需的时间较短,这表明疾病更易于在无标度网络上传播.
4 结束语
本文提出了复杂网络上一种基于再度感染的SIS模型.相对于SIR模型,SIS模型的不同点在于,染病人群一旦被治愈康复后就立刻变成易感人群,从而使得网络中存在这样一种情况:单个易感个体可能多次再度被染病节点所感染.在具有树状分支结构的网络中运用SIS模型,针对某个染病节点,在考虑其感染子节点的同时,也考查其再次感染祖先节点的情况.分别在小世界网络和无标度网络上进行仿真分析,结果表明,对于小世界网络,基于再度感染的SIS模型的稳态感染密度比传统的SIS模型的要大,而且感染周期越短,稳态感染密度越大;而对于无标度网络,虽然基于再度感染的SIS模型的稳态感染密度也比传统的SIS模型的要大,但是,感染周期对于稳态感染密度的影响微乎其微,甚至可以忽略.这是一个很有趣的现象,值得进一步研究.
[1] BAILEY N T J.The Mathematical Theory of Infe-ctious Diseases and Its Applications[M].New York:Hafner Presss,1975.
[2] PASTOR-SATORRASR,VESPIGNANI A.Epidemic dynamics and endemic states in complex networks[J].Physical Review E,2001,63:066117.
[3] PASTOR-SATORRAS R,VESPIGNANI A.Epidemic spreading in scale-free networks[J].Physical Review Letters,2001,86(24):3200-3203.
[4] PASTOR-SATORRASR,VESPIGNANI A.Epidemics and Immunization in Scale-free Networks[M].Berlin:Wiley-VCH,2003.
[5] BOGUÑÁM,PASTOR-SATORRAS R.Epidemic spreading in correlated complex networks[J].Physical Review E,2002,66:047104.
[6] RONI PARSHANI,SHAI CARMI,SHLOMO HAVLIN.Epidemic threshold for the susceptible-infectio-us-susceptible model on random networks[J].Physical Review Letters,2010,104(25):258701.
[7] CALLAWAY DS,NEWMAN M E J,STROGATZ S H,et al.Network robustness and fragility:Percolati-on on random graphs[J].Physical Review Letters,2000,85(24):5468-5471.
[8] COHEN R,EREZ K,HAVLIN S,et al.Resilience of the internet to random breakdowns[J].Physical Review Letters,2000,85(24):4626-4628.
[9] ALEXANDROWICZ Z.Critically branched chains and percolationclusters[J].Physics Letters A,1980,80(4):284-286.
[10] NEWMAN M E J.Spread of epidemic disease on networks[J].Physical Review E,2002,66:016128.
[11] MADAR N,KALISKY T,COHEN R,et al.Immunization and epidemic dynamics in complex networks[J].European Physical Journal,2004,38(2):269-276.
SIS model based on reinfection
ZHUXiao-jun, ZHANGNing(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)
A new SIS model based on reinfection in complex networks was proposed.By using the model in the network with a tree-like sturcture,not only the infection of descendants of an infected node was considered but also the reinfection of ancestor by the infected node was taken into account.Through theoretical analysis and numerical simulation on small-world networks and scalefree networks,it is found that:for small-world networks,the stationary infected density on this new model is larger than that on the traditional SISmodel,and the shorter the infection time is,the gerater the stationary infected density will be;however for the scale-free networks,the stationary infected density on this new model is still larger than that on the traditional SISmodel,yet the effect of the infection time on the stationary infected density can be neglected.
complex network;epidemic spreading;reinfection;ancestor nodes
TP 309.5
A
1007-6735(2011)04-0367-05
2011-03-01
国家自然科学基金资助项目(70971089);上海市重点学科建设资助项目(S30501)
朱晓军(1984-),男,硕士研究生.研究方向:复杂网络.E-mail:xifengpo126@126.com张 宁(联系人),女,教授.研究方向:复杂网络.E-mail:zhangning@usst.edn.cn
