非线性电报方程行波解的定性分析与求解

李 想, 张卫国, 赵 岩

(1.上海理工大学理学院,上海 200093;2.南京信息工程大学数理学院,南京 210044)

非线性电报方程行波解的定性分析与求解

李 想1, 张卫国1, 赵 岩2

(1.上海理工大学理学院,上海 200093;2.南京信息工程大学数理学院,南京 210044)

利用平面动力系统的理论和方法研究了非线性电报方程的有界行波解.分析结果表明,非线性电报方程有且仅有两个有界行波解,并且当耗散作用较大时非线性电报方程的有界行波解呈扭状孤波解形式,而当耗散作用较小时呈衰减振荡解形式.在此基础上,利用假设待定法求出了对应耗散作用较大时方程的一种扭状孤波解的精确解,以及对应耗散作用较小时方程的衰减振荡解近似解.进一步运用齐次化原理,建立反映衰减振荡解精确解和近似解关系的积分方程,得到了衰减振荡近似解的误差估计.

非线性电报方程;平面动力系统;衰减振荡解;近似解;误差估计

1 问题的提出

非线性电报方程[1]

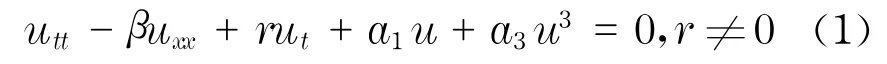
是在铺设大西洋电缆时发现的,它在电报信号传输中有很大的应用.不仅如此,方程(1)还可以描述血液在动脉中的脉动所产生的压力等.

近来有许多学者对方程(1)进行了研究.当r=0时,方程可化为

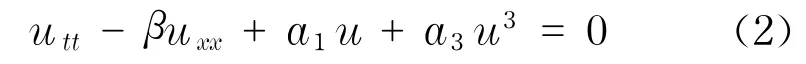
此时系统为保守系统,方程(2)同时也包含物理学上很多著名的方程,如Sin-Gordon方程和Sinh-Gordon方程的近似方程、Φ4方程、Klein-Gordan方程、Laudau-Ginzburg-Ginzburg-Higgs方程和Duffing方程.文献[2-6]中用待定假设方法和齐次平衡法求出了其精确钟状和扭状孤波解.

由于在实际应用中耗散是不可避免的,因而研究r≠0的情况十分必要.从已有文献可知,方程(1)存在扭状孤波解,如文献[3-6]利用待定系数法和齐次平衡法等已求出了其扭状孤波解;最近,文献[7]得到了Fourier级数表示的整体解和长时间整体渐近解,并指出其按指数衰减;文献[8]利用不动点原理研究了耦合的非线性电报方程组,证明了其至少有3个非负周期解.

然而方程(1)究竟存在多少有界行波解,是否有解仍未求出,对于那些未求出的、且有重要应用的解该如何求出,笔者将首先利用平面动力系统理论对非线性电报方程(1)的行波解对应的动力系统作全面的定性分析,画出全局相图,进而研究方程(1)有界行波解的个数和所有可能存在的解形式(包括钟状孤波解、扭状孤波解和衰减振荡解);其次分析耗散作用的大小对方程(1)有界行波解性态的影响,并给出两个反应耗散作用大小的临界值,当|r|大于或等于某临界值时,方程(1)的行波解表现为扭状孤波解,当|r|小于某临界值时,方程(1)的行波解表现为衰减振荡解.在此基础上,给出方程(1)有界行波解的表达式,包括一种扭状孤波解的精确表达式,以及衰减振荡解近似解的表达式;最后给出衰减振荡解近似解的误差估计.这项工作的最大难点是只知近似解,而未知其对应的精确解.为克服这一困难可运用齐次化原理,建立反映衰减振荡解精确解和近似解关系的积分方程,得到衰减振荡解的误差估计.

2 定性分析

设方程(1)有行波解u(x,t)=u(ξ)=u(xct),则其满足

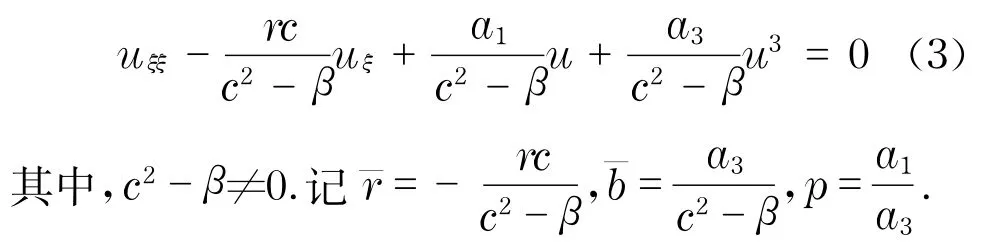
令x=u(ξ)和y=u′(ξ),将方程(1)化为如下等价的平面动力系统

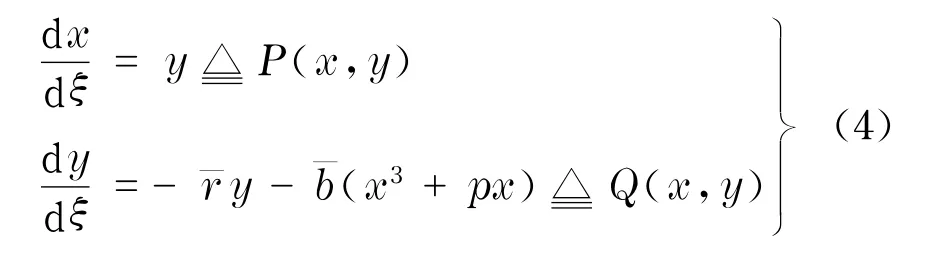
由于系统(4)有限远奇点的个数是由f(x)≜x3+px=x(x2+p)=0的实根个数决定的,本文只研究方程(1)的有界行波解,故以下始终假定p＜0.这样,系统(4)有3个有限远奇点

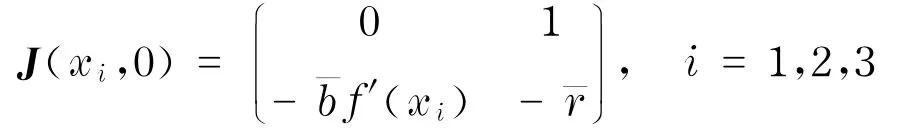
为方便讨论起见,记Di=-f′(x i),i=1,2,3.

利用平面动力系统的理论和方法[9,10],从有限远奇点、无限远奇点和极限环的存在性3个方面对系统进行定性分析.不失一般性,讨论时假设＜0,于是得到命题1～3.

命题1系统(4)有3个不同的有限远奇点,其类型如下:

a.当＞0时,由于det(J(x2,0))=＜0,det(J(x i,0))=-2＞0,i=1,3,且r-＜0,故P2为鞍点,P1和P3在D1=D3＞0时都为不稳定结点,而在D1=D3＜0时都为不稳定焦点.

b.当＜0时,由于det(J(x i,0))=-2＜0,i=1,3,det(J(x2,0))=p b-＞0且＜0,故P1和P3为鞍点,P2在D2＞0时为不稳定结点,在D2＜0时为不稳定焦点.

命题2对系统(4)作Poincaré变换后可得,系,显然,x i(i=1,2,3)是f(x)=0的实根,且在x轴上表现为x1≤x2≤x3,其中,x1,x3关于原点对称.

系统在P i(i=1,2,3)处的雅可比矩阵记为统(4)仅在y轴上存在一对无穷远奇点A i(i=1,2),其中,A1在y轴的正方向上,A2在y轴的负方向上.当＞0时,A i(i=1,2)周围各存在一个双曲型区域;当b-＜0时,A i(i=1,2)周围各存在一个椭圆型区域.此外,Poincaré圆盘的圆周为轨线.

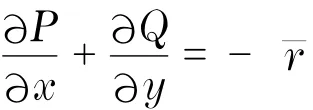
结合前面3个命题,同时为以后说明方便,分别给出=0和＜0时,系统(4)在不同条件下的全局相图,如图1和图2所示.

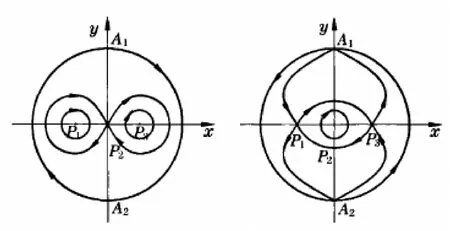
图1 =0时的全局相图Fig.1 Global phase portrait in case of=0

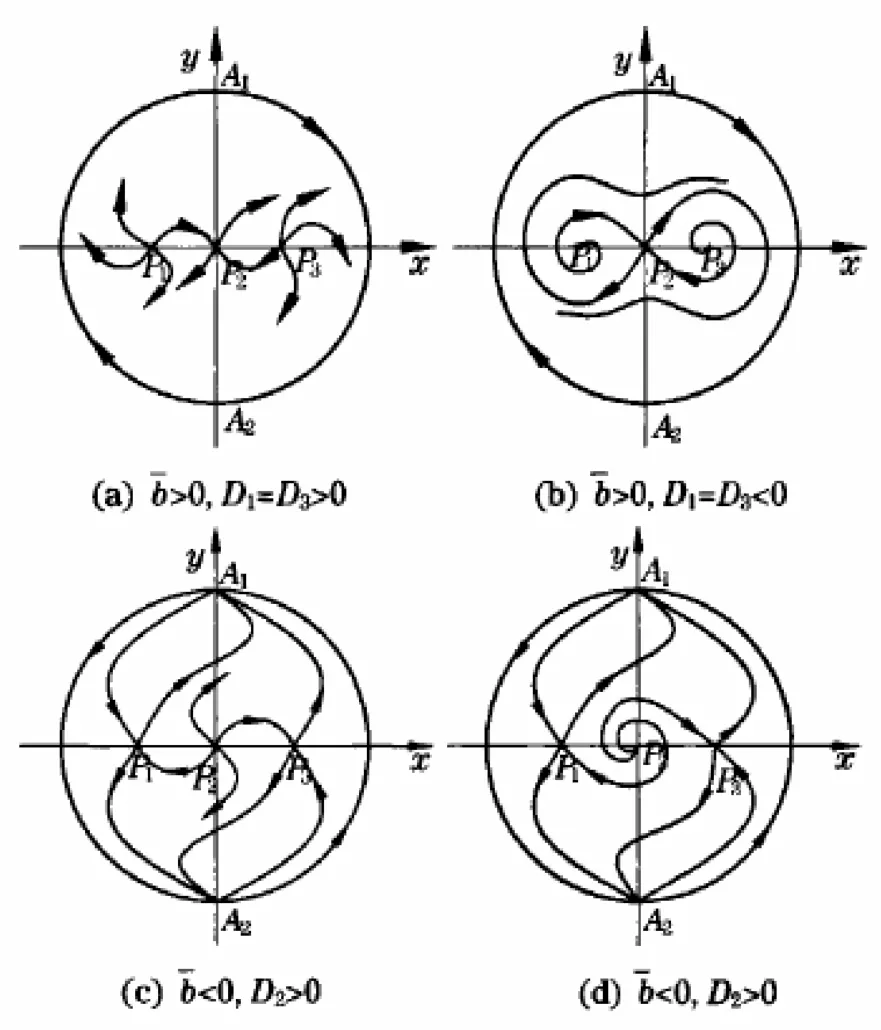
图2 ＜0时的全局相图Fig.2 Global phase portrait in case of＜0

由图1和图2可知,系统(4)有且仅有两条异宿轨L(P i,P2)或L(P2,P i),i=1,3,因系统(4)的有界轨线对应于方程(1)的有界行波解,故可得定理1.

定理1方程(1)有且仅有两个有界行波解.其中,图1(a)中同宿轨L(P2,P2)分别对应两个钟状孤波解;图1(b)中异宿轨L(P1,P3)和L(P3,P1)、图2(a)中异宿轨L(Pi,P2)(i=1,3)和图2(c)中异宿轨L(P2,P i)(i=1,3)分别对应两个扭状孤波解;图2(b)中异宿轨L(Pi,P2)(i=1,3)和图2(d)中异宿轨L(P2,P i)(i=1,3)分别对应两个振荡行波解.

3 有界行波解的性态与耗散系数r之间的关系

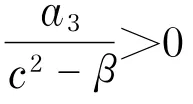
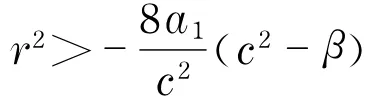
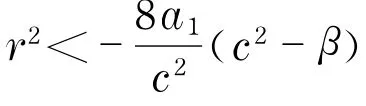
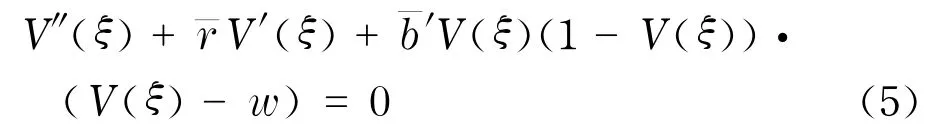
由前面的定性分析知,P2是鞍点,Pi(i=1,3)是不稳定奇点,且系统(4)在(x,y)平面上存在轨线L(Pi,P2)(i=1,3)(见图2(a),图2(b)).因当ξ→-∞时,L(Pi,P2)(i=1,3)分别趋于Pi(i=1,3),当ξ→+∞时,L(P i,P2)(i=1,3)均趋于P2,又x=u(ξ)和y=u′(ξ),故方程(3)不存在满足u(-∞)=u(+∞)的有界解,只可能存在满足以下两种情况的有界解:

情况1u(-∞)=x1,u(+∞)=0;

情况2u(-∞)=x3,u(+∞)=0.

即方程(5)只可能存在满足下列情况的有界解:

情况3V(-∞)=0,V(+∞)=w;

情况4V(-∞)=1,V(+∞)=w.

a.当＜0,＜r1,方程(5)存在单调上升的有界解V(ξ)满足情况3.

b.当＜0,r1＜＜0,方程(5)存在振荡解V(ξ)满足情况3.

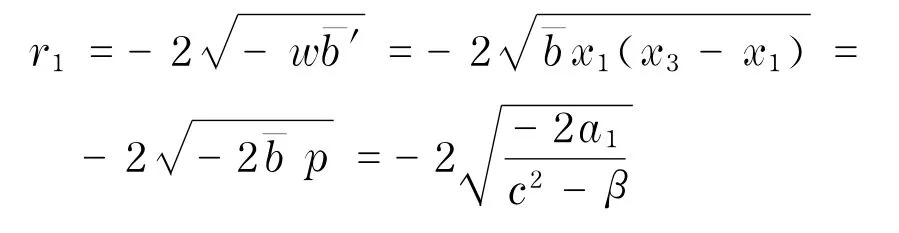
进一步转化到方程(1)中,定理立即得证.

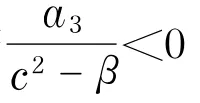
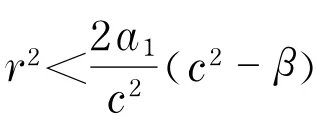
证明证明过程类似定理2.

以方程(1)对应图2(d)焦-鞍轨线L(P2,Pi),i=1,3的振荡行波解为例进行讨论,对于图2(b)中的振荡行波解的衰减性可类似得到.

a.方程(1)对应图2(d)中轨线L(P2,P1)的振荡行波解u(ξ)存在最小值点.该解在的右侧具有单增性,而在其左侧具有衰减性,即在ξ轴上存在无穷可数个极大值点(i=1,2…,+∞)和极小值点(i=1,2,…,+∞),使得

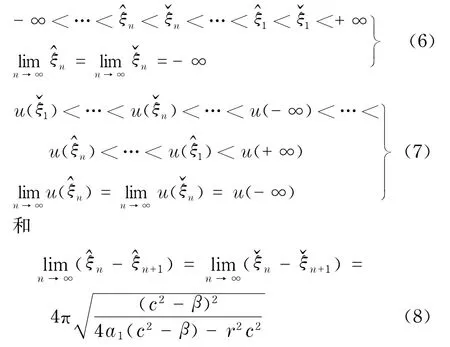
b.方程(1)对应图2(d)中轨线L(P2,P1)的振荡行波解u(ξ)存在最大值点.该解在的右侧具有单减性,而在其左侧具有衰减性,即在ξ轴上存在无穷可数个极大值点(i=1,2,…,+∞)和极小值点(i=1,2,…,+∞),使得

b.证明过程类似a.

综上所述,方程(1)有界行波解的性态由耗散作用的大小决定.当耗散作用较大,即|r|大于某临界值时,方程(1)的有界行波解表现为扭状孤波解;当耗散作用较小,即|r|小于某临界值时,方程(1)的有界行波解表现为衰减振荡解.

4 有界行波解

4.1 钟状和扭状孤波解

利用文献[12]中的方法,分别将

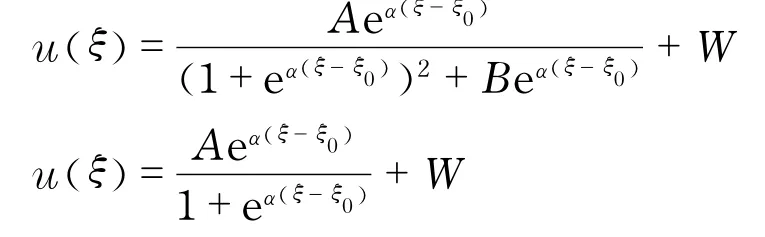
代入到方程(2)中,进行数值计算,可得定理5～7.

容易验证,定理5中所给两个解分别对应图1(a)中的同宿轨L(P2,P2);定理6中所给两个解对应图1(b)中的同宿轨L(P1,P3)和L(P3,P1);定理7中所给两个解式(13)和式(14)分别对应图2(a)中的同宿轨L(P1,P2)和L(P3,P2).

4.2 衰减振荡解的近似解

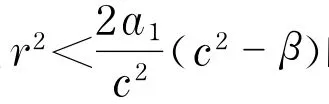
近似表示方程(1)对应焦-鞍轨线L(P2,P3)的衰减振荡解的振荡部分.

将式(11)代入方程(1),略去eα(ξ-ξ0)的高阶项后,可得

当ξ→-∞时,由于式(11)趋于x2=0,故C=0.进一步,可得

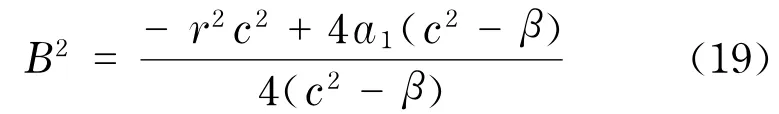
因无论B取正值还是负值,A2sin(Bξ)的值均相同,故以后始终假设B＞0.立即有如下定理:

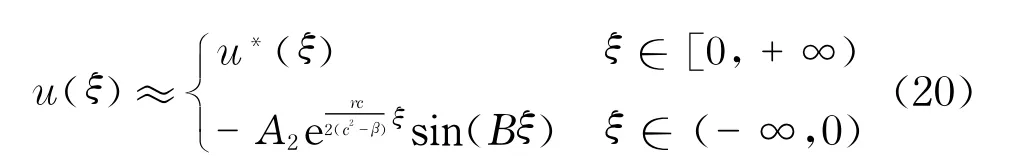
其中,u*(ξ),B,A2分别由式(7)、式(14)、式(13)给出.

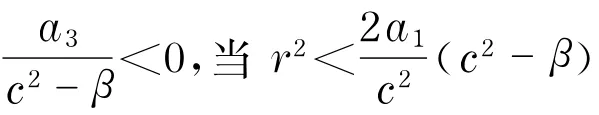
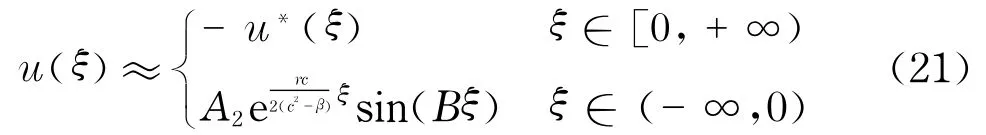
其中,u*(ξ),B,A2同上.

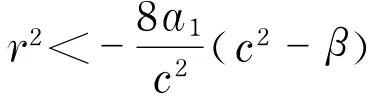
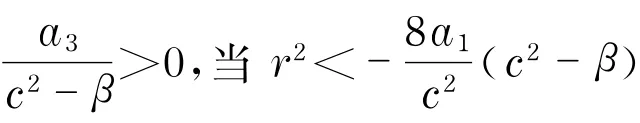
显然,β1,c1和c2分别与定理8中的B,A1和A2相等

因衰减振荡解是有界解,故存在M＞0使得|u(ξ)|＜M.进一步,由式(27),得

式(21)是方程(1)衰减振荡解的振幅估计.由式(21),易见随着ξ＜0的不断减小,u(ξ)将不断接近0.

最后,由式(20)和式(21),得

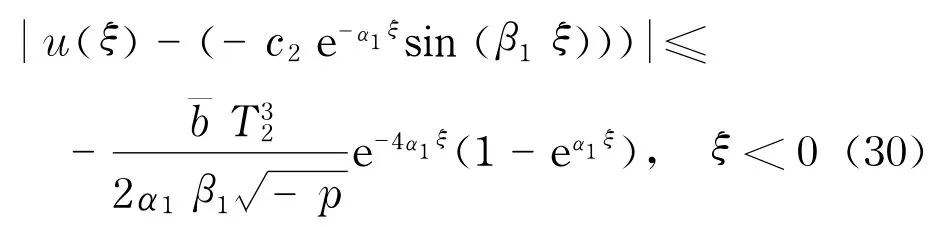
式(30)表明,方程(1)对应图2(d)中焦-鞍轨线L(P2,P3)的衰减振荡解的近似解式(15)与真解间的误差不超过

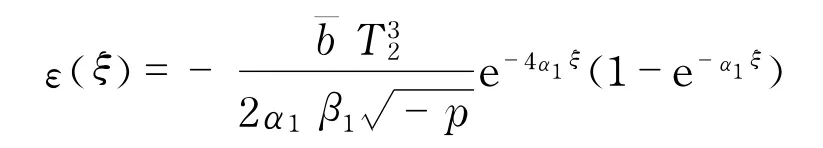
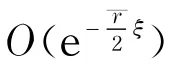
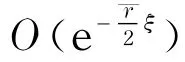
[1] FARLOW SJ.Partial Differential Equations for Scientists and Engineers[M].New York:Wiley Interscience,1982.

[2] 张卫国.几个非线性演化方程的解析解[J].数学研究与评论,1992,12(3):421-426.

[3] 王明亮.一个非线性波动方程的精确解[J].兰州大学学报(自然科学版),1996,32(1):1-5.

[4] 范恩贵,张鸿庆.非线性波动方程的孤立波解[J].物理学报,1997,7(46):1254-1258.

[5] 尚亚东.一类非线性波动方程的显示精确解[J].应用数学学报,2000,23(1):21-30.

[6] ZHANGWei-guo,CHANG Qian-shun,FAN En-gui.Methods of judging shape of solitary wave and solution formulae for some evolution equations with nonlinear terms of high order[J].J Math Appl,2003,287(1):1-18.

[7] 赖绍勇,严勇.非线性电报方程的整体渐进解[J].四川师范大学学报,2004,27(1):446-450.

[8] 王方磊,安玉坤.非线性电报方程组的3个双周期正解问题[J].应用数学与力学,2009,30(1):83-89.

[9] 张芷芬,丁同仁,黄文灶,等.微分方程定性理论[M].北京:科学出版社,1985.

[10] 马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.

[11] 叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1990.

[12] 张卫国.一类非线性发展方程的精确孤波解[J].高校应用数学学报,1996,11(4):399-408.

Qualitative analysis and traveling wave solutions of nonlinear telegraph equation

LIXiang1, ZHANGWei-guo1, ZHAOYan2
(1.College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China;2.Mathematics Department,Najing University ofⅠnformation Science and Technology,Nanjing 210044,China)

Bounded traveling wave solutions of nonlinear telegraph equation were discussed by use of the theory and method of planar dynamical systems.The results indicate that the nonlinear telegraph equation has only two bounded traveling wave solutions.When the dissipation effect is strong,the bounded traveling wave solutions of nonlinear telegraph equation appear as kink solitary wave solutions;and when it is weak,they appear as damped oscillatory solutions.Based on the above discussion,a kink solitary wave solution corresponding to the strong dissipation effect,and approximate damped oscillatory solutions corresponding to the weak dissipation effect were obtained by using undetermined coefficients method.Furthermore,base on homogenization principle,the error estimates of approximate damped oscillatory solutions were given by establishing the integral equations reflecting the relations between exact solutions and approximate solutions.

nonlinear telegraph equation;planar dynamical systems;damped oscillatory solutions;approximate solutions;error estimate

O 175.2

A

1007-6735(2011)04-0372-07

2010-04-28

国家自然科学基金资助项目(11071164);上海市重点学科建设资助项目(S30501);上海市自然科学基金资助项目(10ZR1420800)

李 想(1986-),女,硕士研究生.研究方向:非线性系统的理论与应用.E-mail:lixiang278361999@sina.com张卫国(联系人),男,教授.研究方向:非线性系统的理论与应用.E-mail:zwgzwm@yahoo.com.cn