基于模糊物元理想解法的城市防空掩护目标优选

宋占岭，王亚莉

（1.炮兵指挥学院 河北 宣化 075100；2.宣化科技职业学院 河北 宣化 075100）

现代城市防空作战中，防空兵选择掩护目标需要考虑的主要因素有目标的军事价值、易毁性、易修复性、易攻击性和社会影响等[1]，其实质是一种有限方案多目标多准则决策问题。物元分析法是由我国可拓学工作者创造的多元数据量化决策的一种有效方法，它用事务、特征、量值三要素组成物元来描述事物，通过建立物元分析模型，将多目标决策归结为单目标决策，利用定量数值简洁明确地表示决策结果[2-4]。理想解法通过构造正、负理想方案，然后在众多可行的方案中找到一个最佳方案，使其距正理想方案最近，距负理想方案最远[3-5]。笔者尝试将两种决策方法结合起来，用以解决城市防空掩护目标排序优选问题。

1 基于模糊物元理想解法的决策模型

1.1 预备知识

物元分析理论指出，对给定的事物M，它关于特征C的量值为x，以有序三元组合（M，C，x）作为描述事物的基本元，称为物元。如果其中的特征C具有模糊性，则称之为模糊物元。m个事物的n维模糊物元组合在一起，便构成m个事物的 n维复合模糊物元，记为

式中 ，Mi为第 i个事物 （i=1，2，…，m ）；Cj为第 j个特征 （j=1，2，…，n）；xij为第 i个事物的第 j个特征对应的模糊量值。

1.2 决策模型

1.2.1 构造从优隶属度复合模糊物元

各单项评价指标的模糊量值从属于标准方案对应指标的模糊量值的隶属程度，称为从优隶属度，从优隶属度一般为正值。计算隶属度的方法有很多，为了更充分地反映指标的相对性和合理性，这里采用比值法计算：

对于效益型指标

对于成本型指标

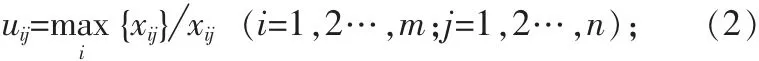
由此得到从优隶属度复合模糊物元：

1.2.2 构造理想方案物元

构造理想方案物元如下：

正理想方案物元

负理想方案物元

对于正理想方案物元，一般有

1.2.3 构造评价指标的权重复合物元

各评价指标对方案评价的影响通过其权重表现出来。目前确定权重的方法主要有主观赋权法和客观赋权法，为充分体现评价指标属性值的作用，在此通过计算标准差得到权重的客观赋权法来确定指标权重。评价指标的权重复合物元记为，

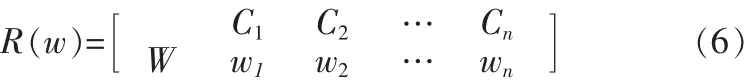
这里，wj为第j评价指标权重

aj为第j个指标在不同评估对象中的标准差

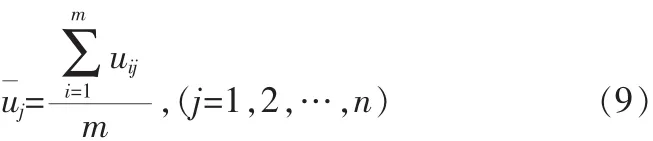
1.2.4 计算各方案与理想方案的距离

利用欧氏加权距离来描述各方案与理想方案的距离。

方案Mi与正理想方案M+的距离

方案Mi与负理想方案M-的距离

1.2.5 计算方案与理想方案的相对贴近度

方案Mi与理想方案的相对贴近度

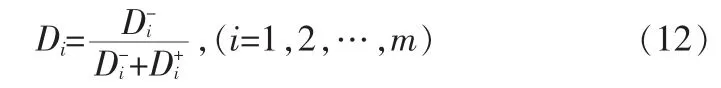
显然，根据相对贴近度数值可对各方案进行排序优选。

2 实证分析

以文献[1]中城市防空掩护目标优选为例，说明模型应用。

根据文献[1]表 1中的数据得到 4个掩护目标（T1、T2、T3、T4）5个评价指标（军事价值 f1、易毁性 f2、易修复性 f3、易攻击性 f4和社会影响f5，其中只有易修复性 f3属成本型指标，其余皆为效益型指标）的复合模糊物元。

根据（1）（2）可得到从优隶属度复合模糊物元

根据（4）（5）得到正、负理想目标物元

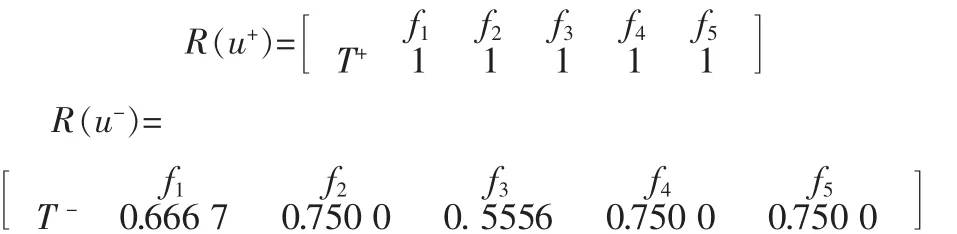
根据（7）（8）（9）得到第 j评价指标均值、标准差及权重，如表1所示。

表1 第j评价指标均值、标准差及权重Tab.1 Expectations and standard deviations and weights of the evaluation indexes

据此得到评价指标的权重复合物元

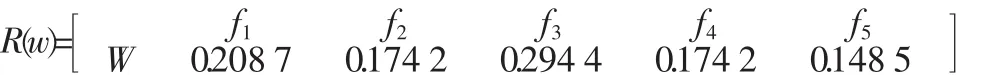
根据（10）～（12）计算得到各目标物元与理想目标物元的距离、相对贴近度，如表2所示。

表2 各目标物元与理想目标物元的距离、相对贴近度Tab.2 Distances and the relative contact degrees of the real target matter-elements and the ideal target matter-elements

显然，各备选目标的排序为：目标 T2＞目标 T3＞目标 T1＞目标 T4。与文献[1]的计算结果相同。

3 结束语

城市防空作战，防空兵在选择掩护目标时，需要综合考虑目标的军事价值、易毁性、易修复性、易攻击性和社会影响等，不能仅凭某项结果主观臆断。笔者在模糊物元分析理论的基础上，利用理想点法思想构造了理想物元，为更好地体现原始评价指标值的价值，利用标准差法求取指标权重，借助于欧氏范数体现各评价方案与理想方案的距离，以此计算相对贴近度，通过相对贴近度值，实现对方案的排序优选。实例表明该法能够做到主观判断与客观计算相结合，定性分析与定量计算相结合，使决策结果合理可信，具有较高的实用价值。

[1]宋占岭，王永良，王亚莉.基于信息熵与TOPSIS法的城市防空掩护目标优选[J].指挥控制与仿真，2010，32（3）：22-23.

SONG Zhan-ling， WANG Yong-liang， WANG Ya-li.Covered targets priority of the city air defense based on iInformation entropyand TOPSIS method[J].Command Control＆ Simulation， 2010，32（3）：22-23.

[2]杨兆兰.多目标决策模糊物元分析 [J].甘肃联合大学学报，2005，19（3）：12-14.

YANG Zhao-lan.Fuzzy matter-element analysis on Multiobjection decision[J].Journal of Gansu Lianhe University，2005，19（3）：12-14.

[3]程启月.作战指挥决策运筹分析[M].北京：军事科学出版社，2004.

[4]魏世孝，周献中.多属性决策理论方法及其在 C3I系统中的应用[M].北京：国防工业出版社，1998.

[5]宋占岭，王永良，王亚莉.基于三角模糊数TOPSIS的火炮发射阵地优选[J].兵工自动化，2010，29（8）：35-38.

SONG Zhan-ling，WANG Yong-liang，WANG Ya-li.Gun launching position priority based on triangular fuzzy numbers and TOPSIS[J].Ordnance Industry Automation， 2010，29（8）：35-38.

[6]薛定宇.高等应用数学问题的 MATLAB求解 [M].北京：清华大学出版社，2004.