分块NSA在人脸识别上的应用

童啸

（江苏省常熟职业教育中心校 江苏 常熟 215500）

身份识别是我们每个人在日常生活中经常遇到的问题，例如我们经常使用身份证、工作证、信用卡、个人设置密码等方法来证明身份。但是，它们不仅携带不便、不易保管、记忆复杂，而且容易丢失、忘记、被他人窃取和盗用，这些方法都不够保险，为了解决这些困难，人们提出了一种根据人体自身的生物特征来进行身份识别的方法，即所谓的生物特征识别技术[1-3]。其中人脸识别是生物特征识别技术中的重要研究课题之一，也是近年来的一个研究热点[3]。

人脸识别是模式识别领域中的一个重要课题，具有非常广泛的研究前景。近几年来，人脸识别得到了很大的发展，提出了很多优秀的算法。其中，Turk等人提出的特征脸方法（Eigenfaces）方法[4]和 Belhumeur等人提出的 Fisher脸（Fisherfaces）方法[5]是应用最为广泛的两种的算法。简单说，特征脸方法就是通过主成分分析（Principal Component Analysis，PCA）来进行人脸识别，计算向量样本的总体协方差矩阵，其最大的d个特征值对应的特征向量作为鉴别矢量集，然后样本在鉴别矢量集上投影，得到的d个系数就是抽取出的特征。Fisher脸方法采用线性判别分析（Linear Discriminant Analysis， LDA）[6]方法从高维特征空间里提取出最具有判别能力的低维特征。近来Fisher脸又有新的发展[7-9]。但是，LDA有以下几个缺点：1）处理高维图像时容易产生“小样本问题”，即样本维数大大超过训练图像个数的问题，因此在小样本情况下，如何抽取Fisher最优鉴别特征成为一个公认的难题[10-13]；2）线性判别分析LDA最多有C-1个判别特征，但是在一些高维空间中往往是不够的[1]；3）在计算类间散布矩阵时，仅仅只考虑了类的中心值，并没有有效地捕获类的边界结构，而这些边界结构已经被证明在分类中是非常有用的。这时LDA方法并不能取得很好的结果[14]。为了克服这些缺点，取得更好的识别率，Li[15]等提出了非参数子空间分析（nonparametric subspace analysis，NSA）方法。

本文秉承核判别分析的思想，先对图像进行分块，对分块得到的子图像矩阵再用NSA方法进行鉴别分析——这种方法称为分块NSA。这样做主要基于下面两点考虑，一是在人脸识别中当人脸表情和光照条件变化较大时，由于通常的NSA方法抽取的是图像的全局特征，所以其识别效果并不理想。而实际上当人脸表情和光照条件变化时，仅部分人脸区域变化明显，而其它部分变化不大，甚至无变化，对划分后的子图像进行鉴别分析可以捕捉人脸的局部信息特征，从而有利于识别；二是对原始图像进行分块，不仅可以方便地以2的指数次幂降低图像向量的维数，而且可以以2的指数次幂增加子图训练样本的数目，缓解小样本问题，减少问题的复杂度。在ORL和XM2VTS人脸库上验证了该方法在识别性能上优于NSA和分块LDA方法。

1 NSA方法

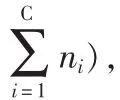
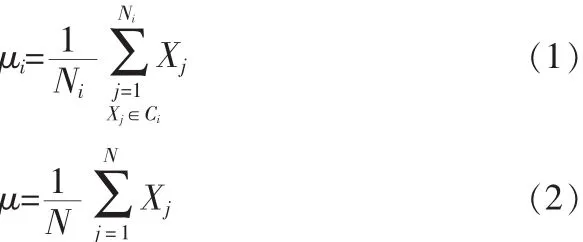
则所有训练图像样本的类间散布矩阵SNb和类内散布矩阵Sw为

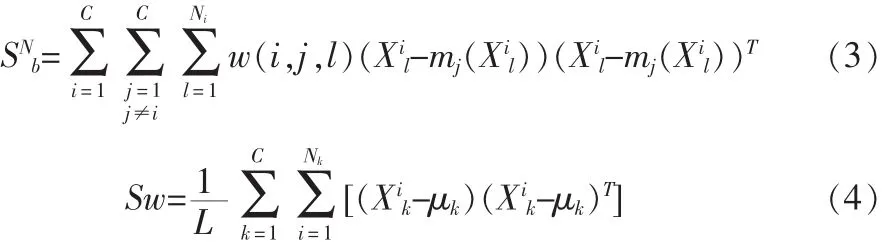
其中，权值函数 w（i，j，l）和 K 最近邻均值 mj（xil）的定义如下：

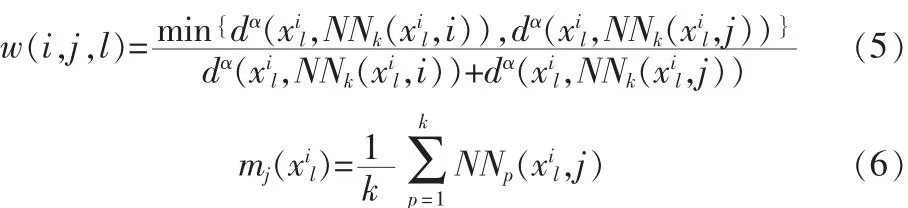
式中α是一个从零到无穷大变化的且控制权值方面距离比变化速度的一个参数，d（v1，v2）是矢量 v1和 v2的欧几里得距离，NNp（xil，j）是第 j类中第 p 幅人脸到人脸矢量 xil最近邻距离。

从式（3）我们发现：第一，如果我们选择k=Ni和设置所有的权值函数值都为1时mj（Xil）就变为第j类的样本均值。这就意味着NSA方法基本上是LDA方法的泛化。第二，与LDA相比，LDA最多只能提取C-1个判别特征，而NSA打破了使用所有的训练样本来构造类间散布矩阵Sb的固有限制，仅仅使用类中心来构造。因此，更多的特征能被提取出来进行判别从而加强了分类性能。第三，NSA方法比LDA方法更好的利用不同类别的边界结构信息。这个可以从Xil-mj（xil）的定义中看出。

由式（3）和（4）我们可以定义最优判别准则函数为：

其中，W是最优辨识投影空间。我也可以将J（W）转化成广义特征值问题，定义如下

从式（8）我们可以看出，当Sw可逆时，可以写成如下的标准特征值求解问题

计算Sw-1SNb的特征分解，得到d个最大特征值对应的特征向量。

从上述分析，我们注意到k近邻点k的取值在某种程度上影响着算法的识别性能。因此NSA方法就是讨论如何选择适当的k值，从而得到更高的算法识别率。

2 分块NSA

2.1 图像分块

分块LDA思想是先将一个m·n的图像矩阵I分成p·q分块图像矩阵（类似于线性代数中矩阵的分块），即

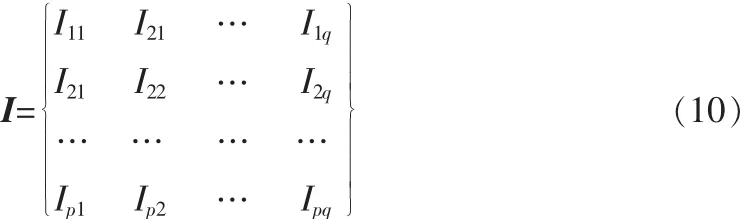
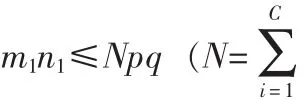
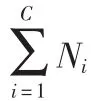
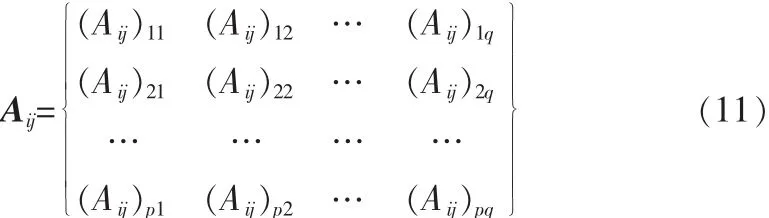
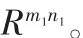
2.2 特征提取

把所有训练图像样本的子图像矩阵视为训练样本图像向量，再施行NSA方法。则所有训练图像样本的子图像矩阵的类间散布矩阵为

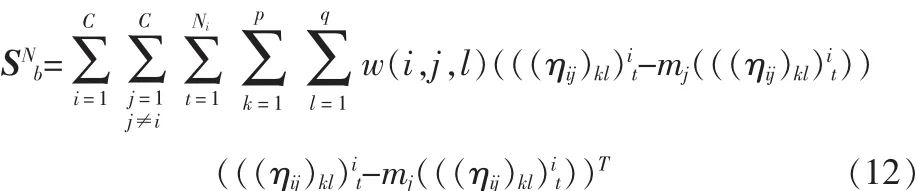
所有训练图像样本的子图像矩阵的类内散布矩阵Sw为

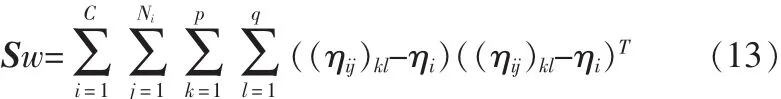
接下来的任务与NSA的类似，计算在最佳投影矩阵下的前d个最大特征值所对应的特征向量Z1，Z2，…，Zd，设最优投影矩阵 Q=[Z1，Z2，…，Zd]，则训练样本 Aij的特征矩阵为

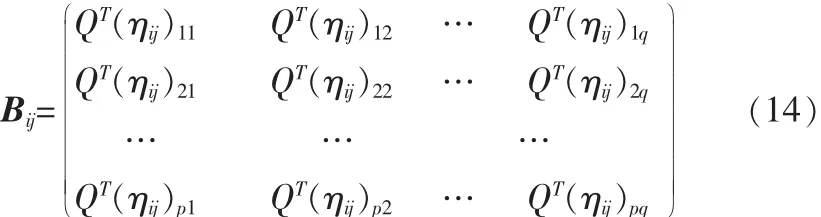
2.3 分类

通过NSA的特征提取后，每个图像对应一个特征矩阵，对此特征矩阵，利用最小距离分类器进行分类。

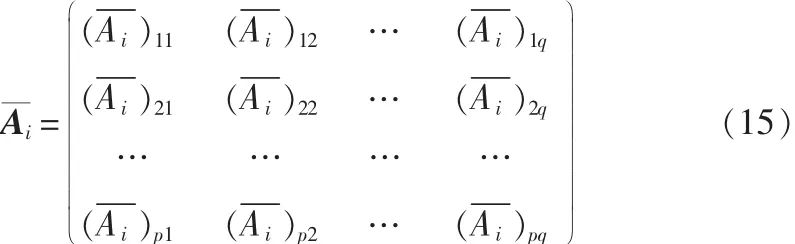
其特征矩阵（pd×q）为：

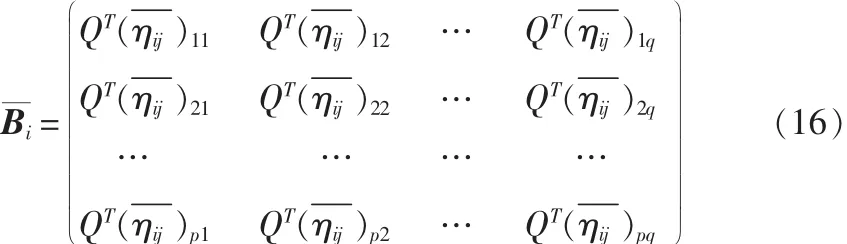
测试样本：

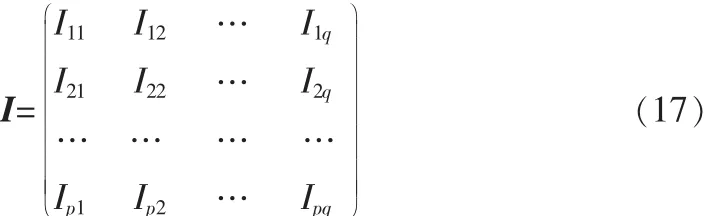
特征矩阵（pd×q）为：

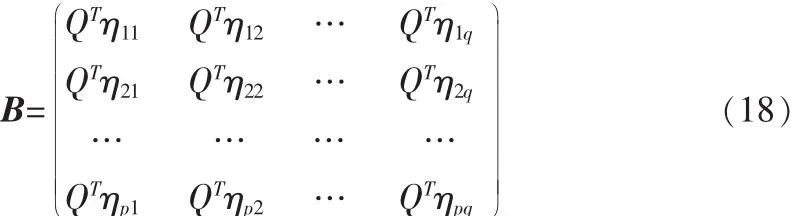
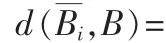
此外，我们得指出的是NSA是分块NSA的特殊情况，因此，本文的分块NSA方法是NSA方法的推广。

3 实验结果与分析

3.1 ORL上人脸识别实验结果

ORL库由40人的脸部图像组成，每人10幅112×92的图像，其中有些图像拍摄于不同的时期，脸部表情、细节及姿态均有变化，深度旋转与平面旋转可达20°，人脸尺度有最多10%的变化[16]。如图1是ORL数据库中的一些人脸图像：

由于本试验的目的之一是为了检验本文算法对光照的敏感程度，故在图像规一化的过程中，我们对图像的灰度不做任何处理。试验中采用每人的前5幅图像作为训练样本，后5幅作为测试样本，这样训练样本和测试样本总数均为200。表1给出了对原始图像矩阵进行2×2，2×4和4×4三种分块后得到的结果。3种情况下分块子矩阵的大小分别为56×46，56×23，28×23。 取 k 个投影轴，则所得的整体投影特征向量的维数分别是 56×k，56×k和28×k。 采用的分类器是最小距离分类器。从表中结果我们发现本文方法的结果优于NSA和分块LDA方法的结果。

表1 ORL数据库中各算法的识别率Tab.1 Recognition rate of every algorithm with ORL database

图2给出了对ORL原始图像矩阵进行2×2，2×4和 4×4三种分块后得到的结果。3种情况下分块子矩阵的大小分别为 56×46，56×23，28×23。取 k 个投影轴，则所得的整体投影特征向量的维数分别是 56×k，56×k和 28×k。 采用的分类器是最小距离分类器。从表中结果我们发现本文方法的结果优于NSA和分块LDA方法的结果。

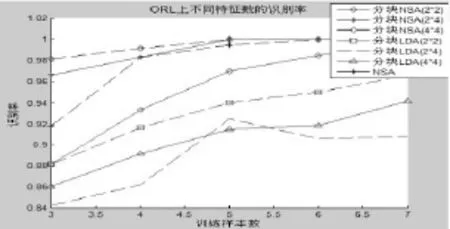
图2 ORL数据库中各算法的识别率Fig.2 Recognition rate of every algorithm with ORL database

3.2 XM2VTS上人脸识别实验结果

XM2VTS人脸库包括295人在4个月时间内4次录制的人脸和语音数据[16]。在每个时间段，没人被记录了2个头部旋转的视频片段和6个语音视频片段。其中每幅图像的分辨率为55×51。图3是XM2VTS数据库中的一些人脸图像。

由于本试验的目的之一是为了检验本文算法对光照的敏感程度，故在图像规一化的过程中，我们对图像的灰度不做任何处理。试验中采用每人的前4幅图像作为训练样本，后4幅作为测试样本，这样训练样本和测试样本总数均为295×4。 表 2 给出了对原始图像矩阵进行 5×3，5×17 和 11×17三种分块后得到的结果。3种情况下分块子矩阵的大小分别为 11×17，11×3，5×3。 取 k 个投影轴，则所得的整体投影特征向量的维数分别是11×k，11×k和5×k。采用的分类器是最小距离分类器。从表中结果我们发现本文方法的结果优于NSA和分块LDA方法的结果。

图3 XM2VTS数据库中的人脸图像Fig.3 Image of ORL XM2VTS database

表2 XM2VTS上跟算法的识别率Tab.2 Recognition rate of every algorithm with XM2VTS database

图4给出了对XM2VTS原始图像矩阵进行5×3，5×17和11×17三种分块后得到的结果。3种情况下分块子矩阵的大小分别为 11×17，11×3，5×3。 取 k 个投影轴，则所得的整体投影特征向量的维数分别是11×k，11×k和5×k。采用的分类器是最小距离分类器。从表中结果我们发现本文方法的结果优于NSA和分块LDA方法的结果。

图4 XM2VTS上跟算法的识别率Fig.4 Recognition rate of every algorithm with XM2VTS database

实验结果表明，本节的新算法在选取不同分块做人脸识别时均可以得到不错的识别率。

通过上述实验我们可知，分块NSA方法是NSA方法的推广，它的识别率要高于NSA的识别率，因为我们首先对训练样本图像进行分块，这样就很容易的提取到训练样本图像的局部特征，而这些局部特征更能反映出图像的差异性。

4 结束语

本文提出了分块NSA方法并将其应用于人脸识别。所提出的方法是一种直接基于子图像矩阵的非线性特征提取方法，与以往的基于图像向量的非线性特征提取方法 （比如NSA方法）相比，由于对原始图像进行分块，可以方便地在较小的图像上进行特征提取方法，使其过程简便，如分块NSA可以避免使用矩阵的奇异值分解理论。在ORL人脸库和XM2VTS人脸库上的实验结果表明，所提出的方法的识别率比NSA和分块LDA的识别率要高。

[1]苑玮琦，柯丽，白云.生物特征识别技术[M].北京：科学出版社，2009：1-5.

[2]田捷，杨鑫.生物特征识别技术理论与应用[M].北京：电子工业出版社，2004：1-5.

[3]王映辉.人脸识别—原理、方法与技术[M].北京：科学出版社，2010.

[4]Turk M，Pentland A.Face recognition using eigenfaces[C]//Proceedings of the IEEE Computer Society Conference on ComputerVision and Pattern Recognition （CVPR’91）.Washington，1991：586-591.

[5]Belhumeur P N，Hespanha J P，Kriegman D J.Eigenfaces vs fisherfaces：recognition using class specific linear projection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19（7）：711-720.

[6]Swets D L，Weng J.Using discriminant eigenfeatures for image retrieval[J].IEEE Trans.Pattern Analysis and Machine Intelligence，1996，18（8）：831-836.

[7]Chen L F，Liao H Y，et al.A new LDA-based face recognition system which can solve the smalls ample size problem[J].Patern Recognition，2000，33（9）：1713-1726.

[8]YU Hua，YANG Jie.A direct LDA algorithm for high-dimensional data with application to face recognition[J].Pattern Recognition，2001，34（10）：2067-2070.

[9]JIN ZHong，YANG Jing-yu.Face recognition based on the uncorrelated discriminant transformation[J].Pattern Recognition，2001，34（7），1405-1416.

[10]CHEN Li-Fen，LIAO H-Y，KO M-T，et al.A new LDA-based face recognition system which can solve the small sample size problem[J].Pattern Recognition，2000，33（10）：1713-1726.

[11]YU Hua，YANG Jie.A direct LDA algorithm for highdimensional data-with application to face recognition[J].Pattern Recognition，2001，34（10）：2067-2070.

[12]Yang J，Yang J Y，Ye H，et al.Theory of fisher linear discriminant analysis and its application[J].Acta automatic Sinica，2003，29（4）：482-493.

[13]YANG Jian，YANG Jing-yu.Why can LDA be performed in PCA transformed space?[J].Pattern Recognition，2003，36（2）：563-566.

[14]Marinez A M，Kak A C.PCA versus LDA[J].IEEE PAM I，2001，23（2）：228-233.

[15]LI Zhi-feng，TANG Xiao-ou.Nonparametric discriminant analysis for face recognition[J].Pattern Analysis Machine Intelligence， 2009， 31（4）： 755-761.

[16]Friedman N，Geiger D，Goldszmidt M.Bayesian network classifiers[J].Machine Learning，1997，29（2/3）：131-163.