基于Bayesian非局部先验的低剂量X-射线CT成像

高大志，陈阳，杨刚，卢光明

1.南京军区南京总医院 医学影像科，江苏 南京 210002；2.东南大学生物医学工程学院医学信息研究所，江苏 南京 210000

基于Bayesian非局部先验的低剂量X-射线CT成像

高大志1，陈阳2，杨刚1，卢光明1

1.南京军区南京总医院 医学影像科，江苏 南京 210002；2.东南大学生物医学工程学院医学信息研究所，江苏 南京 210000

目的降低病人在CT扫描中所受的辐射剂量。方法在低剂量的扫描条件下，由于有效投影信息的缺少，CT图像易受到量子噪声的影响。本文提出了一种新的非局部先验Bayesian重建算法来提高CT图像重建质量。结果与传统的图像重建方法比较，本文提出的重建方法，能够利用目标图像中更多形态结构的全局信息来构建先验项，从而克服了传统图像重建信息局限性的缺点。结论试验证明本文所提出的CT图像重建方法在低剂量扫描条件下具有很好的表现。

螺旋CT；CT成像；Bayesian；低剂量扫描

本文导读 >>

课题背景：目前低剂量X-射线CT扫描由于能够减少病人的扫描辐射伤害而日益受到人们的关注。课题受国家自然科学基金（No.81000636）资助，主要针对低剂量CT扫描中由于有效光子数降低而导致成像质量下降的问题所做的初步研究。

实验设计/论文构思：基于Bayesian重建理论，通过引入图像的全局信息来改善成像质量，并与当前国际上流行的其他图像重建方法进行比较和分析。

1 研究背景

X-射线CT扫描在临床上的广泛应用，使得其中的辐射伤害日益受到人们的关注[1]。而目前螺旋CT扫描的普及也进一步增加了病人在扫描中所受的辐射剂量[2]。因此，低剂量扫描条件(降低参数mAs、电压kV)下的CT成像越来越越多地得到医生和病人的重视[3]。然而，采用传统的FBP重建算法，在低剂量扫描条件下, 投影数据g容易受到量子噪声的影响，重建出的图像f质量会明显下降，出现大量噪声和星条状伪影。基于统计学的迭代重建能够针对系统模型的物理效应和探测数据、噪声的统计泊松特性建立数学模型，同时可以通过Bayesian后验定理引入图像空间的先验信息，解决图像重建中由于噪声而导致的病态问题，其重建的图像质量要优于传统的FBP方法[4-13]。Bayesian重建就是在迭代重建中引入图像空间的先验信息项来抑制噪声，基于此，我们可以构建以下用于图像重建的后验概率：

其中g和f分别为测量观察数据和待重建的目标衰减图像。P(f)代表马尔可夫随机场(Markov Random Fields，MRF)先验分布。Z为正常数或者配分函数，为似然分布， 即为 MRF先验能量或能量方程，为像素点处的先验能量方程，全局参数β控制MRF先验对重建图像正则化作用的程度。可以根据(1)和(2)式建立相应的后验能量方程：

2005年，Buades等人设计了一种新的非局部去噪方法用于图像的去噪处理[14]。在他们的非局部思想的启发下，本文提出一个用于低剂量X-射线CT图像Bayesian重建的非局部二次先验模型，该模型不仅能使用目标图像中单个像素之间的灰度差信息，而且能够有效的利用图像中连接和连续的全局信息。相关的模拟试验表明：对于低剂量投影数据的X-射线CT图像重建，本文所提出的非局部先验Bayesian重建法在降低噪声效果和保持边缘方面均具有非常好的表现。

1.1 传统局部先验模型

基于MRF理论，当目标图像f满足先验假设时，公式(2)中的能量方程U(f)具有最小值且相应的先验分布(2)式达到最大值。而像素j点处的先验能量方程U(f,j)通常等于以像素j与其邻域Nj内个点的差为自变量的势能函数v( )的加权和：

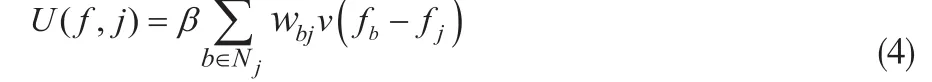
可以通过选择不同的势能函数v(t)来设计用于Bayesian重建的不同先验模型。如果势能函数v(t)为二次的V(t)=t2形式，先验P（f）即为简单的二次QM平滑先验。我们也可通过使用选择一些非二次势能函数v(t)来使用非二次先验[3-10]，如Huber先验的势能方程：

其中，δ为控制势能函数的阈值参数。

公式(4)中的权值量wbj为表示图像中像素b和j的相互关系的正常数。通常设定wbj的值同像素b和j之间距离成反比。下面即为广泛应用于图像重建和恢复中的传统局部先验的八邻域归一化权值图和四邻域归一化权值图:

以上的先验模型只能为图像重建提供固定的局部的先验信息。二次局部QM先验通过重建过程中的一个平均化的作用提供平滑的先验信息，从而易于导致图像边缘细节和噪声同时平滑掉的过平滑效应。具有边缘保持作用的局部非二次先验则会因为无法有效的区分噪声和一些较细微的细节而为图像重建带来负面的伪影效果。

1.2 非局部二次先验模型

在建立非局部先验的过程中，一方面需要选择一个较大的邻域来包含图像中的更多几何形态信息，另一方面通过计算像素b的邻域和j的邻域的一个相似性测度，而不是用以上1.1节所述的像素间二维空间距离的简单反比例量来计算权值wbj。根据以上的非局部先验设计思路，我们可以根据(6)～(11)式为Bayesian重建设计新的非局部先验。

式中UNL(f)为非局部先验的能量函数， 这里Nj通常选择一个较大尺寸的邻域以引进更多的结构信息，wbj设为（1-0）二值函数，代表先验中像素b和j之间的权值，nb和nj为设定的以像素b和j为中心的方形邻域， f(nb)和f(nj)为此两个邻域中所有像素灰度值数组，‖f（nb）-f（nj）‖代表此两个像素灰度值数组的加权欧几里得距离。

在选择一个较大邻域的基础上，此非局部先验不仅比较图像中两个像素的灰度值，而且通过比较此两个像素邻域的相似性来计算势能函数中的权值量。如图1所示，在每组图中，左边的图为原图，右边的图描绘了左图中心点邻域中各点在非局部先验模型中权值的取值情况。可以看出，权值一般分布于比较相似的结构处，对于两个具有相似周围结构的像素点，此两个像素点在先验中的权重较大，该非局部先验模型能够考虑到图像中的一些较大的几何结构形态的全局信息，能够对图像重建中的病态问题提供更为有效的正则化。

图1 权值分布图

在使用文中所述的非局部先验模型的情况下，目标图(每组图中左图)中的中心点的邻域权值分布如每组图中的右图所示，设定nb和nj的大小分别为31×31和7×7时，(a) 当中心点位于一条竖直的边缘上时，权值分布在此竖直边缘线上；(b) 当中心点位于倾斜的边缘时，权值分布在倾斜的边缘线上；(c) 当中心点位于特定纹理结构时，权值分布在特定的纹理结构上。

2 实验与分析

2.1 CT迭代重建

在X-射线CT重建中，我们可以把测量投影数据理解为服从独立泊松分布的随机变量。第i对投影数值gi可以认为是一个期望的泊松随机数，这个是一个自变量为衰减图像的方程[7-8]。似然方程PL(g/f)定义为在已知f的情况下，得到测量数据g的概率。基于此，可以得到以下各式：

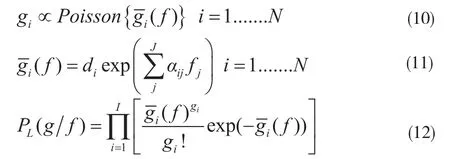
其中N是探测器对的数目，j是目标图像像素的数目，αi,j是在理想条件下图像像素点j被探测器对i探测到的几何概率。f2(g/f)对应于(1)中P(g/f)，其对数似然能量方程为：

可以通过对后验能量ψ的最大化迭代运算来重建出目标图像f：

然而，由(7)～(11)式可知，此非局部先验能量中的权值项wbj的取值由目标图像f所决定，增加了直接求导计算的难度，实际试验我们采用如下步骤的重建算法：

（1）设定迭代初始项f°。

（2）权值项w的更新：在构建此非局部先验能量时，对于目标图像f中的每一个像素对(fb，fj)，用迭代过程中的当前值的和公式(7)～(11)来计算wbj。

（3）目标图像f项的更新：

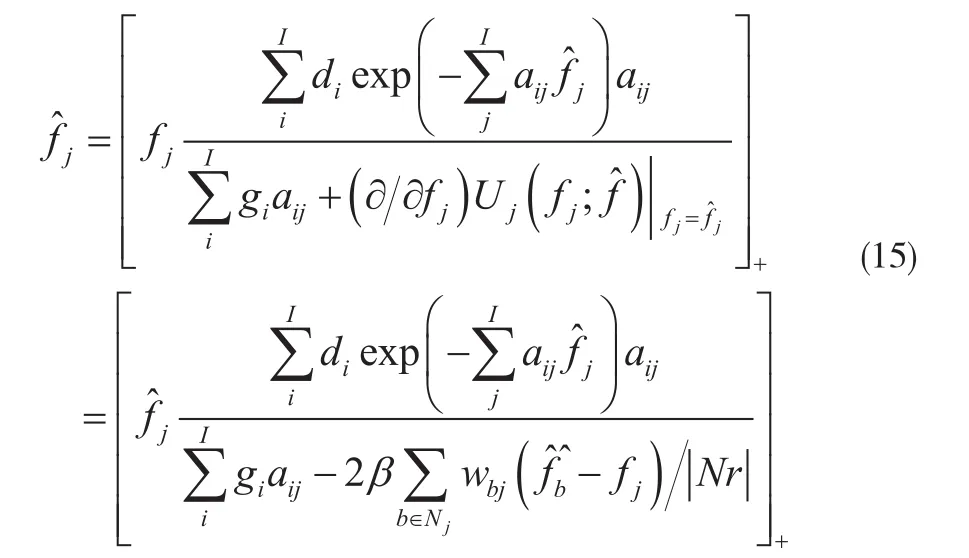
2.2 模拟试验

在实验中,我们使用单排探测器CT，X-射线源和探测器距离设为100cm，旋转中心到探测器距离设为40cm，相邻探测器距离为1mm，扫描系统为具有367个径向取样和360个角采样的系统。图2 (a)为试验中使用的256×256体模数据图像，表示一个Shepp-Logan体模截面图，图像素点取值范围为0～240；图2(b)为对应的正弦图（sinogram）投影数据。基于此模拟的两个不同剂量(投影数据数值总和分别为1.2×108和1.5×108)的投影数据，投影数据中均加入了10%服从泊松分布的随机噪声。转换概率矩阵A为一个平行带状积分几何模型，通过(12)式中的模型进行计算。

图 2 体模图像(a)与对应的平行束投影正弦图(b)

图3和图4分别显示了使用以上的两个不同剂量投影数据下的重建结果，使用Ramp滤波器的FBP重建(FBP1重建)，使用Hann滤波器的FBP重建(FBP2重建)和使用二次局部QM平滑先验，非二次局部Huber先验，MRP以及非局部先验的Bayesian重建图像。对于后面4种Bayesian重建，选取第250次迭代的重建图 (在实验中，当迭代到第250次时，重建图像已趋于稳定)。从图3和图4可以看到 探测数据在FBP重建图像中易出现大量噪声和星条伪影，相对于使用Ramp滤波器的FBP1重建(图3 (a)和图4 (a))；使用Hann滤波器的FBP2重建(图3 (b) 和图4(b))能够更好的抑制噪声；采用QM先验重建的图像(图3 (c) 和图4(c))中出现了导致结构信息模糊的过平滑效应；对于使用非二次Huber先验的重建(图3 (d) 、图4 (d))和MRP(图3 (e) 、图4 (e))的重建来说，可以从结果图像中观察到块状的不规则伪影区域和阶梯状的伪影。另一方面，可以清楚的观察到，使用本文提出的非局部先验重建的图像(图3 (f)和图4 (f))具有更加均匀的背景区域和更加清晰的边缘。采用该非局部先验的重建不仅能够克服QM平滑先验的过平滑效应，而且能够在很大程度上解决非二次Huber先验和MRP所导致的阶梯状伪影的问题。

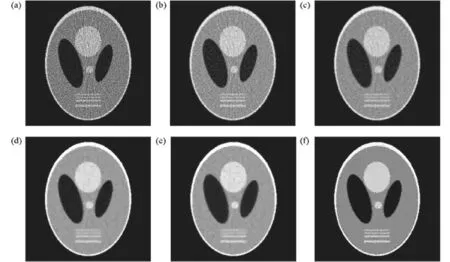
图 3 使用总和为1.2×108探测数据sinogram的重建结果

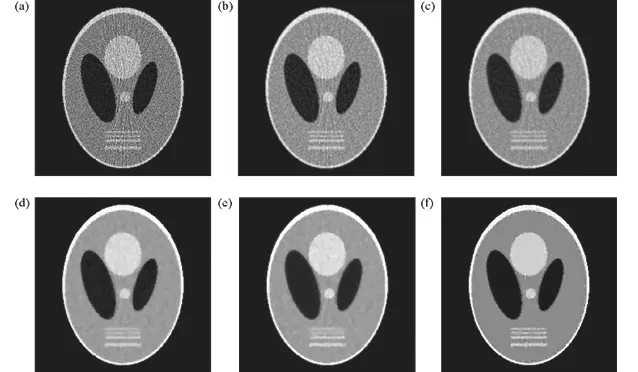
图 4 使用总和为1.5×108探测数据sinogram的重建结果

在重建试验中，使用不同的体模数据需要选择不同的参数，试验中依据产生最高信噪比SNR（计算公式见(16)）的原则手工设定参数，试验中，信噪比SNR的计算公式为：

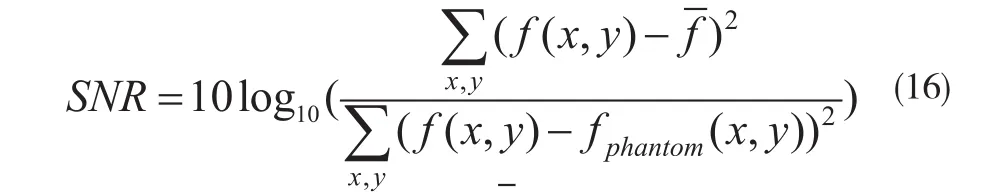
对于此两种不同计数量的sinogram数据，在二次QM先验重建中，设定全局参数β的值分别为2×10-2和1.8×10-2；在采用非二次Huber先验的重建中，全局参数的值同QM一样，设定全局参数δ的值分别为1.6和1.3；在采用MRP的重建中，设定全局参数β的值分别为40和20；在采用非局部先验的重建中，设定全局参数β的值分别为0.5和0.6，式(6)～(8)中参数n的取值分别为0.6和1.1，设定式(6)中nj的大小为11×11，设定(9)～(10)中的两个比较邻域nb和nj的大小为7×7。

表1给出了对于此两种不同计数量的sinogram数据。由以上所有重建图像对于真实体模图像的信噪比SNR，可以看出使用本文提出的方法的重建图像具有更高的信噪比。表2给出了不同重建方法在P4 1.6 GHz、512Mb RAM 的硬件环境下，matlab7.0的软件环境下运行得到重建结果所需的CPU时间。可以看出本文所提出的非局部先验Bayesian重建需要更多的计算时间。

表1 两种不同总探测量的sinogram数据，重建图像相对于图2中真实体模图像数据的信噪比

表2 重建中使用不同方法所需CPU时间(s)

3 结论

相对于通常意义上的二次或者非二次的局部先验，本文提出的新的非局部先验能够利用目标图像中更多形态结构的全局信息来构建先验项，能够引入更多更全面的先验信息，从而克服了局部先验信息局限性的缺点。基于模拟数据和真实数据的试验表明：相对于使用普通的二次平滑先验及非二次边缘保持先验的重建，使用该混合先验重建的CT图像能够更好保持边缘信息，消除背景噪声，且具有更高的信噪比。

进一步的工作包括，对图像重建中由非局部先验引进的参数进行有效的估计，减少使用非局部先验重建的计算量；应使用更多的真实CT图像扫描数据来测试该非局部先验重建方法在临床试验中的效果。

[1]Linton OW, Mettler Jr FA. National conference on dose reduction in CT, with an emphasis on pediatric patients[J]. Am JRoentgenol,2003,181:321-329.

[2]Jung K, Lee K, Kim S, et al. Low-dose, volumetric helical CT:image quality, radiation dose, and usefulness for evaluation of bronchiectasis[J]. Invest Radiol,2000,35:557-563.

[3]Lu H, Hsiao I, Li X, et al. Noise properties of low-dose CT projections and noise treatment by scale transformations[C].2001 IEEE Nuclear Science Symp.Conf.,2001.p.1662-1666.

[4]Beekman FJ,Kamphuis C.Ordered subset reconstruction for X-ray CT[J]. PhysMed Biol,2001,46:1835-1855.

[5]Stan Z. Li. Markov Random Field Modeling in image Analysis[M]. Tokyo: Springer-Verlag, 2001:1-40.

[6]Black. M. J and Rangarajan A. Unification of line process,outlier rejection, and robust statistics with application in early vision [J]. Int. Journal of Computer Vision, 1996, 9:57-91.

[7]Nuyts J, De Man B, Dupont P, et al. Iterative reconstruction for helical CT:a simulation study[J].Phys Med Biol,1998,43:729-737.

[8]Sukovic P, Clinthorne NH. Penalized weighted leastsquares image reconstruction in single and dual energy X-ray computed tomography[J].IEEE Trans Med Imaging,2000,19(11):1075-1081.

[9]Lange K.Convergence of EM image reconstruction algorithms with Gibbs smoothness[J]. IEEE Trans Med Imaging,1990,9:439-446.

[10]Erdo-gan H, Fessler JA.Monotonic algorithms for transmission tomography[J]. IEEE Trans Med Imaging,1999,18(9):801-814.

[11]Alenius S, Ruotsalainen U, Astola J. Attenuation correction for PET using countlimited transmission images reconstructed with median root prior[J]. IEEE Trans Nucl Sci,1999,46:646-651.

[12]Yu DF, Fessler JA.Edge-preserving tomographic reconstruction with nonlocal regularization[J].IEEE Trans Med Imaging,2002,21(2):159-173.

[13]Li SZ. Markov random field modeling in image analysis[M].Tokyo: Springer-Verlag,2001:1-30.

[14]Buades A, Coll B, Morel JM. A nonlocal algorithm for image denoising[J]. Proc IEEE Int Conf Comput Vision Pattern Recognit,2005,2:60-65.

[15]Chen Y,Ma J,Feng Q,et al.Nonlocal prior Bayesian tomographic reconstruction[J]. J Math Imaging Vision,2008,30:133-146.

[16]周显国,等.贝叶斯决策分析在医学步态分析中运动目标检测的应用研究[J].中国医疗设备,2010,25(9):16-19.

Low-dose X-ray Computed Tomography Based on Bayesian Nonlocal Prior

GAO Da-zhi1, CHEN Yang2,YANG Gang1, LU Guang-ming1
1.Medical Imaging Department, Nanjing General Hospital of Nanjing Military Area Command, Nanjing Jiangsu 210002,China;2.Institute of Medical Information&Technology, School of Biomedical Engineering, Southeast University, Nanjing Jiangsu 210000,China

R319；TN919.81

A

10.3969/j.issn.1674-1633.2011.02.006

1674-1633(2011)02-0021-04

2010-10-20

2010-11-23

国家自然科学基金（81000636）资助。

本文作者：高大志，硕士研究生。

作者邮箱：njdazhi@hotmail.com

Abstract:ObjectiveTo reduce the radiation dose delivered to the patients during the application of computed tomography (CT).MethodsCT images can be easily degraded by the quantum noise under low X-ray dose scan protocols. Statistical reconstructions outperform the traditional filtered back-projection(FBP) reconstructions by accurately modeling the scan system and the measurement statistics. This paper aims to improve the CT reconstruction using a new nonlocal prior statistical reconstruction approach.ResultsCompared to traditional reconstruction approaches, the proposed nonlocal prior can impose an effective regularization for reconstructions by exploiting the image global information adaptively.ConclusionExperimentation validates that the proposed CT reconstructions have excellent performance with low-dose scan protocols.

Key words:spiral CT; CT imaging; Bayesian arithmetic; low-dose scanning