基于可拓理论的不相容问题的求解初探

姜 跃

(云南财经大学高等职业技术学院，云南昆明650221)

基于可拓理论的不相容问题的求解初探

姜 跃

(云南财经大学高等职业技术学院，云南昆明650221)

传统的人工智能方法在处理矛盾问题、策略的生成方面有许多不足.如何更准确地表示知识和智能化的推理已成为当今研究的热点和难点问题.可拓学的的创立为知识表示和推理的理论研究提供一条新的途径，用可拓学思想对知识进行表示，对不相容问题进行分析，并给出了检查含圈矛盾知识的算法.

可拓学;知识表示;矛盾知识

利用计算机进行策略生成和评价已成为决策科学化和智能化的必然趋势.在“决策支持系统”、“群决策支持系统”、“专家系统”等应用领域中，传统知识库和专家系统的特征是求解相容问题，即对无矛盾问题求解，而对矛盾问题提供解决方案是非规范知识处理的难点问题之一，其研究对现代科学的发展具有重要意义.蔡文教授等建立了一门原创性横断学科——可拓学，它是我国科学家建立的、影响深远的学科［1－3］.可拓学具有形式化、逻辑化和数学化的特点.可拓集合描述事物性质的可变性，描述量变和质变，也是人工智能解决问题的定量化工具.

本文针对传统的知识表示和推理方法在解决矛盾知识方面的不足，将可拓学理论应用于知识表示方法，对可拓知识表示的继承循环这一矛盾问题的化解进行研究.

1 可拓学的知识表示

可拓学突破经典数学的框架，以基元为逻辑细胞，研究其性质并引入相应的变换与运算，以解决纯数学所不能解决的矛盾问题［4］.

为了让计算机能处理矛盾问题，可拓逻辑必须具有2个特点:①用形式化模型;②要考虑事物的内涵，要能表达“变”的推理规律.为此，可拓逻辑汲取了形式逻辑的形式化特点，采用了辩证逻辑研究内涵的思想，形成化矛盾问题为不矛盾问题的逻辑［5］.基于这一思想，本文用三元组 g=(Γ，C，V)或g=(Γ，C，C(Γ))对可拓知识进行表示，其中Γ的称为对象名，它可以是事物或知识，也可以解释为关系，C为特征向量，用于刻画对象，V为关于C的特征向量值.以对象名Γ，n个特征c1，c2，…，cn和相应的量值 v1，v2，…，vn构成的 n 维阵列，即

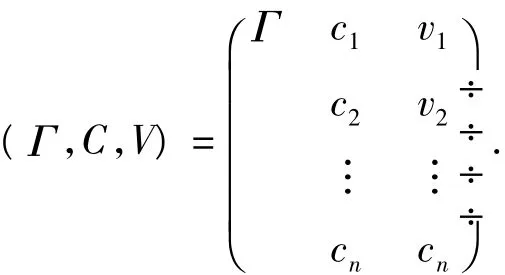
作为描述对象Γ的基本元，称为n维基元，也可表示成为:

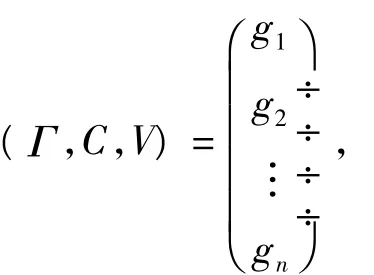
2 不相容问题的定义及形式化模型

在可拓学中，矛盾问题是指事物现有状态与期望状态之间存在差异，也就是在现有条件下无法实现期望的目标.可用形式化模型记为:

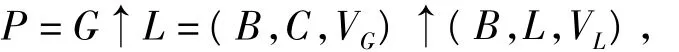
其中，P表示矛盾问题;L为影响目标实现的主客观因素，即条件，且 L⊆{L1，L2，…，Ln};G 为在现有条件 L下，期望实现的目标，且 G⊆{G1，G2，…，Gn};B为基元，C为基元B的特征向量，且C⊆{C1，C2，…，Cn}，VG为基元B关于C的期望取值，且VG⊆{VG1，VG2，…，VGn}，VL为基元B在现有条件L下关于C的取值，且 VL⊆{VL1，VL2，…，VLn}.

在可拓学中又将矛盾问题分为不相容问题和对立问题.

1)不相容问题是指在现有条件下无法实现单个目标.可用形式化模型记为:

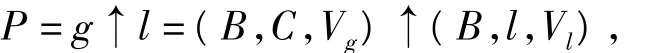
其中，g 为单个目标，g∈{G1，G2，…，Gn};

2)对立问题是指在现有条件下无法同时实现多个目标.可用形式化模型记为:

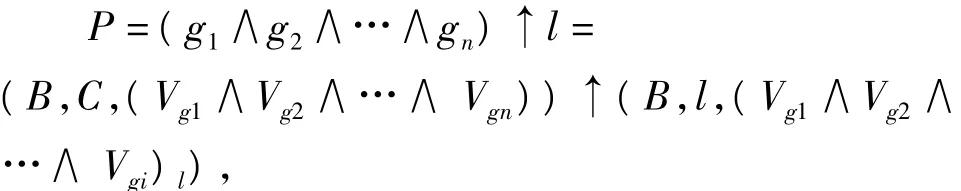
其中，i＜n，gj∈{G1，G2，…，Gn}，1≤j≤n.

3 不相容问题的相关网表示

本节利用基元的相关性，构造不相容问题的相关网，对其目标和条件进行分析，对于含圈的矛盾知识进行分解，转换为相关树，从而为可拓知识推理奠定基础.

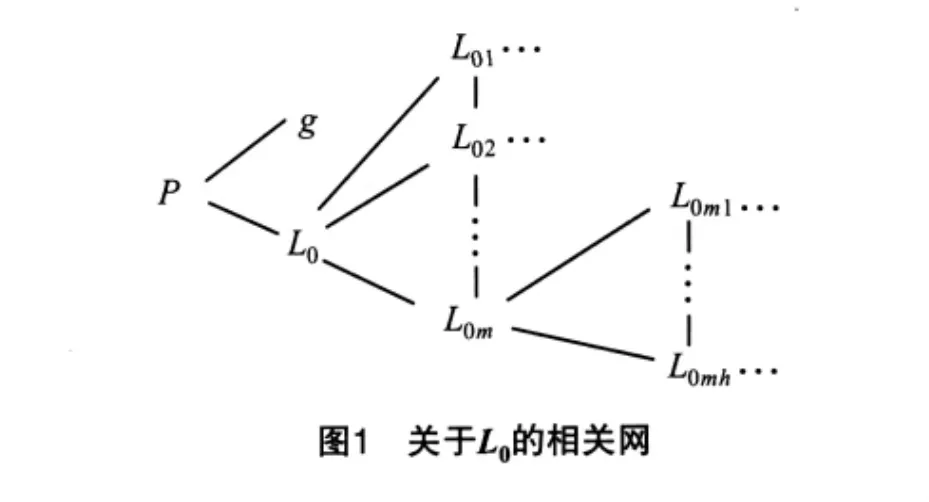
依据相关网的概念，若对相关网中某一结点e进行分析，可将相关网中的结点分为以下几类:

1)父结点f相同，子结点彼此之间没有关系的结点，如:动也会影响到销量，反之亦然.于是，可得到如下关于利润、售价、销量的相关网，如图2所示.

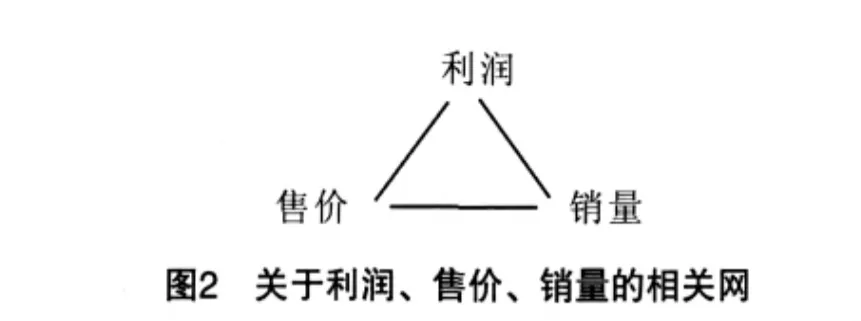
设求解的问题是，提高利润.而由如上的相关网可知，利润、售价和销量之间的关系构成了一个环.而环上各结点发生了变化都会影响到其它结点，由此产生循环继承问题.为了解决好这一类问题，本文依据可拓学求解不相容问题的基本思想解决提高利润问题.首先，以利润为根结点进行相关分析，得到关系:利润与售价相关，利润与销量相关;其次，将相关网中利润与售价、利润与销量之间的关系断开，并检测售价与销量之间是否有关系，如果有，将其断开(之所以能将其断开，是因为可将售价与销量之间的关系通过利润与售价、销量之间的函数关系间接地反映);接着，分别以售价、销量为根结点，重复如上2步，直到相关网中所有结点均检测完毕.这样，就将相关网转换成了相关树，如图3所示.在此相关树上，可以很方便地对问题进行定量和定性的分析.

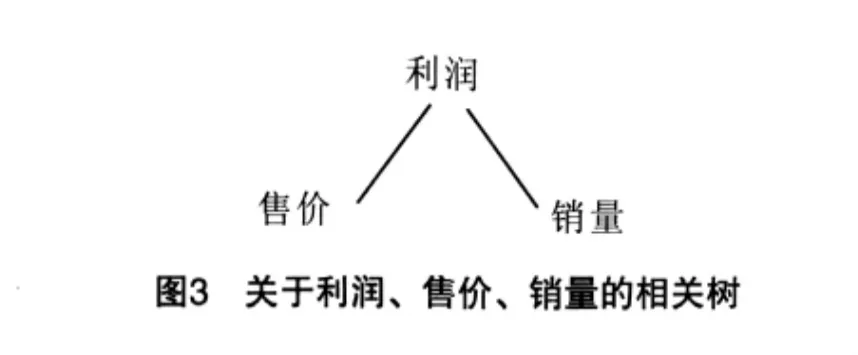
综上所述，相关网转换成相关树算法的采用广度优先搜索方法的基本思想如下:

1)从相关网的根结点出发，将相关网中的根结点、根结点分支和分支结点复制成相关树中的根结点、根结点分支和分支结点;

2)在相关网中，删去根结点、根结点分支，并检测各分支结点的特征向量值之间是否相关，若相关，删去该相关关系.在相关网中，再次检查各分支结点的下一级结点是否有相同的，若相同，则依据相关关系对下一级结点进行复制，确保上下级之间的相关关系信息不丢失;

3)分别以各分支结点作为根结点，重复1)，2)两步，直到所有结点都在相关树中为止.

4 结语

可拓学虽然是一门新兴学科，但是通过几十年的发展，已经形成了基本的理论框架，用以解决矛盾问题.本文将可拓学的思想应用于人工智能研究中，对知识的继承循环的矛盾知识进行分析研究.做了尝试性的工作，还有大量的问题需要进一步探索，为今后人工智能的研究提供一种更为广阔的应用前景.

［1］蔡文.可拓论及其应用［J］.科学通报，1999，44(7):673－682.

［2］CAI Wen.Extension theory and its application［J］.Chinese Science Bulletin，1999，44(17):1 538 －1 548 .

［3］AGRAWAL R，IMIELINSKI T，SWAMI A N.Mining association rules between sets of items in large databases［C］//Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data.Washington DC，USA，ACM Press，1993:207 － 216.

［4］蔡文，杨春燕，何斌.可拓逻辑初步［M］.北京:科学出版社，2004.

［5］蔡文.可拓集合和不相容问题［J］.科学探索学报，1983(1):83－97.

(责任编辑庄红林)

Theory Based on Extension of the Incompatibility Problem Solving

JIANG Yue
(Vocational and Technical College，Yunnan University of Finance and Economics，Kunming 650221，China)

The traditional artificial intelligence methods in dealing with contradictions and strategy have a lot less than the formation.More accurate representation of how knowledge and intelligent reasoning has become the hotspot and difficult issues.Extension of the creation of knowledge representation and reasoning for the theory provides a new way.Thought this paper，the extension of the knowledge，the analysis of incompatibility and the algorithm are given to check contradiction knowledge with the circle.

extenics;knowledge representation;incomplete knowledge

TP 18

A

1672－8513(2011)02－0129－03

10.3969/j.issn.1672 －8513.2011.02.013

2010－12－30.

国家自然科学基金(60903131).

姜跃(1958－)，女，副教授.主要研究方向:人工智能与数据库.