一个新混沌系统的非线性耦合同步的研究

张旭东，俞建宁，郭兰平，彭建奎，张建刚

(1.兰州交通大学 数理与软件工程学院，甘肃兰州730070;2.甘肃联合大学数学与信息学院，甘肃 兰州730000)

一个新混沌系统的非线性耦合同步的研究

张旭东1，俞建宁1，郭兰平1，彭建奎2，张建刚1

(1.兰州交通大学 数理与软件工程学院，甘肃兰州730070;2.甘肃联合大学数学与信息学院，甘肃 兰州730000)

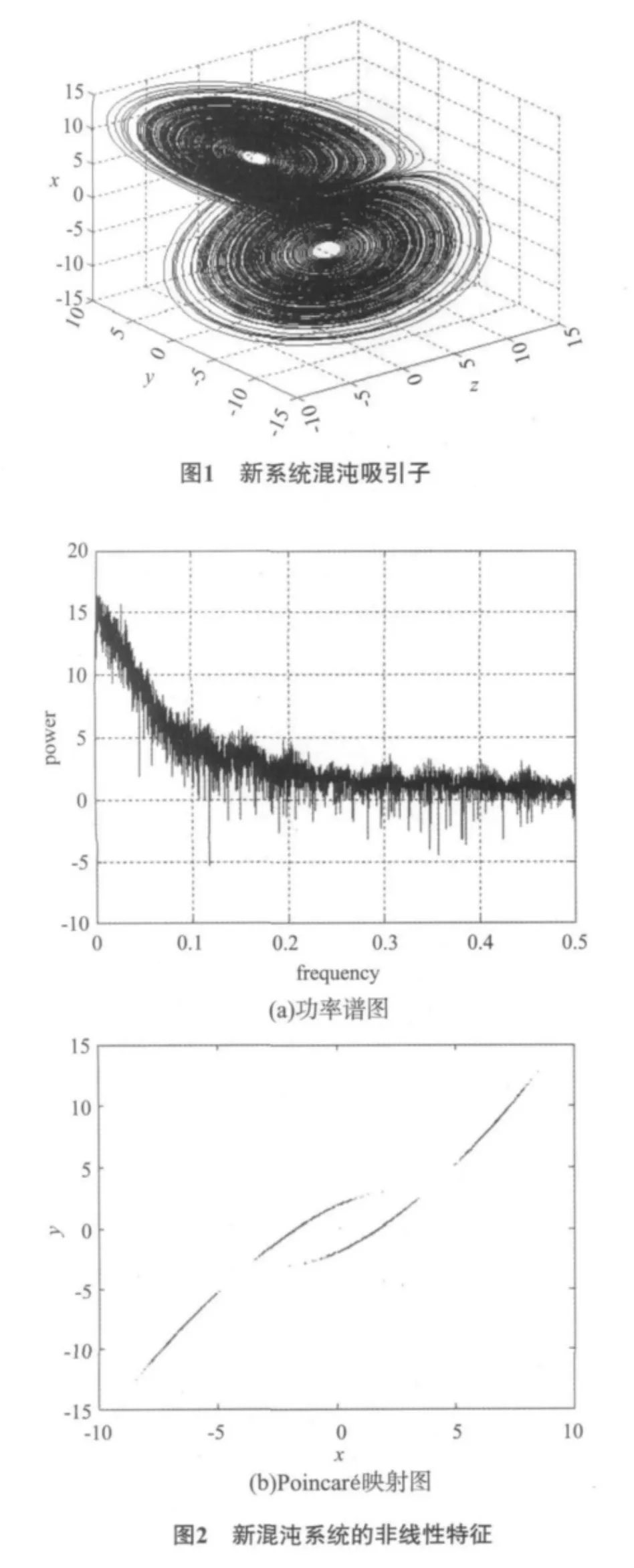
讨论了一个新混沌系统的非线性特征，给出该系统的相图、功率谱、Poincaré映射及Lyapunov指数，运用非线性函数耦合法讨论了该混沌吸引子的混沌同步问题，通过数值模拟分析表明初始值和耦合强度因子的选择对实现混沌同步的影响较小，证实该混沌同步方法的有效性.

新混沌系统;非线性耦合;Poincaré映射;Lyapunov指数谱

混沌具有丰富的非线性动力学特性，在过去的40年中，混沌在数学和工程通信等方面得到了广泛的研究，混沌研究包括混沌同步、混沌生成、混沌分析、非线性电路实现等［1－3］.1990 年，Pecora和 Carroll［4］首次提出了混沌同步的一种有效方法，并在随后在实验中观察到混沌同步现象，近年来，随着混沌同步研究的不断深入，人们发现混沌同步在保密通信和振荡发生器的设计等领域都有着巨大的应用前景，于是混沌同步成为了各个领域研究的热点.美国科学家Lorenz［5］于1963年得到第1个混沌系统－Lorenz系统以来，许多新的自治混沌系统也相继提出并得到了广泛的研究，并且这些系统的吸引子也被实验电路所验证［6－9］，2007 年，褚衍东、李险峰等［9］提出了一个类似Lorenz系统但也不拓扑等价的新混沌系统(Chu系统)，并用电子电路实现了该系统，由于Chu混沌系统是一个新的混沌系统，并有着多种复杂的动力学行为，对于这个混沌系统及吸引子网络的同步研究具有重要意义.

1 Chu混沌系统的描述

褚衍东等提出的混沌系统(Chu系统)动力学描述为:

2 新混沌系统的非线性耦合同步

给定一个混沌连续时间系统

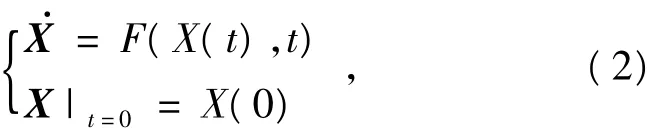
其中，X∈ Rn为 n维状态矢量，F:Rn→ Rn，将F(X(t)，t)适当分离为

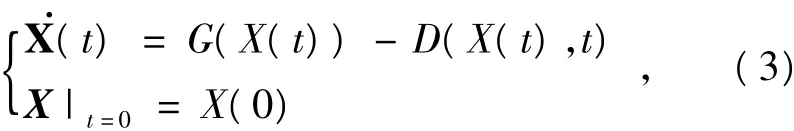
这里G(X(t)，t)是经过特殊配置的F(X(t)，t)的线性部分，即

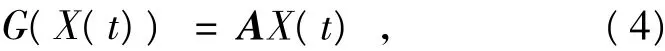
其中，A为满秩的常数矩阵，通过适当的分离配置可使A的所有特征值均具有负实部.

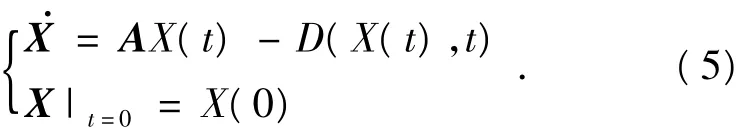
本文讨论的同步是完全同步，即恒等同步.对于原连续时间混沌系统(5)，利用非线性函数D(X1)与D(X2)的差作为耦合函数，构造如下2个新系统:

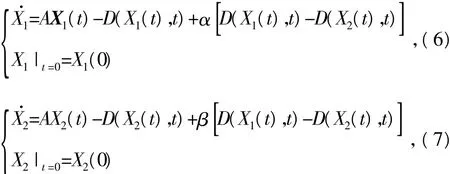
其中，X1，X2∈Rn为所构造新系统的状态矢量，耦合强度因子α，β为常值，当α=β，2个新系统(6)和(7)实现状态同步，即X1(t)=X2(t)时，新系统(6)和(7)与原系统(2)保持一致，则称这种混沌同步为对称耦合同步;反之，当α≠β，2个新系统(6)和(7)实现状态同步，即X1(t)=X2(t)时，称之为非对称耦合同步.

取新系统(6)和(7)之间的同步误差e(t)=X1(t)－X2(t)，当e(t)充分小时，其变化规律近似用线性方程表示为

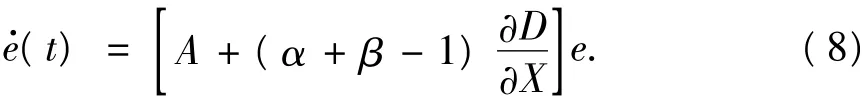
当α+β=1时，e(t)的0点为平衡点.由于A的所有特征值实部均为负值，根据线性系统稳定性准则，同步误差的0点为渐近稳定，当t→∞时e(t)→0，此时实现了新系统(5)和(6)的状态矢量X1(t)和X2(t)的完全同步.当α+β≠1时，需计算方程(8)的条件Lyapunov指数，当条件Lyapunov指数均为负值时，同步状态具有稳定性.

在 Chu系统(1) 中，当参数a=5，b=16，c=1时Chu系统处于混沌状态.将系统(1)的右端函数分离为函数G(X(t)，t)和D(X(t)，t)如下:

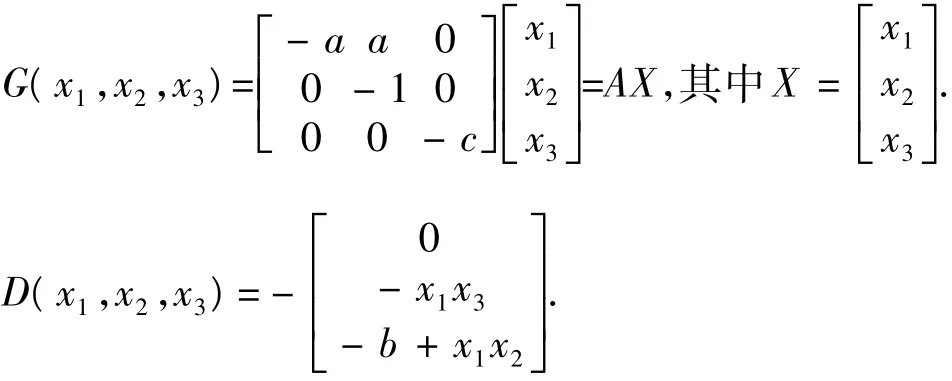
矩阵A的特征值(－5，－1，－1)均为负实数，此时按照系统(6)和(7)，通过非线性耦合构造2个新系统，即

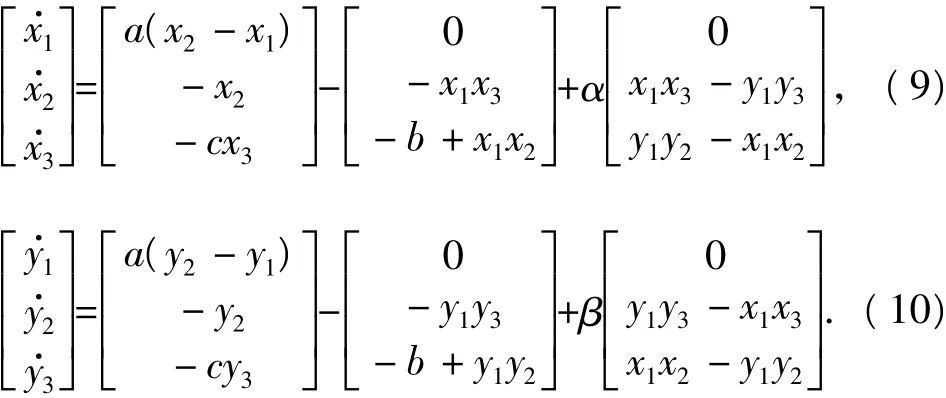
按照方程(8)列出同步误差微分方程

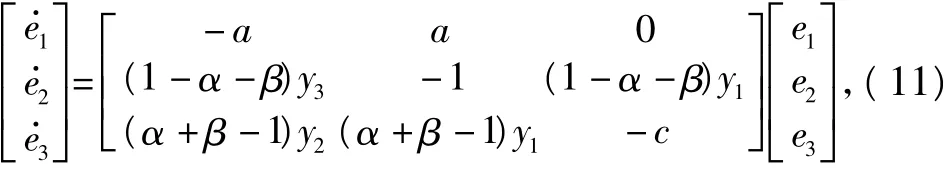
下面讨论不同初值和不同耦合强度因子的选取对实现系统的影响.

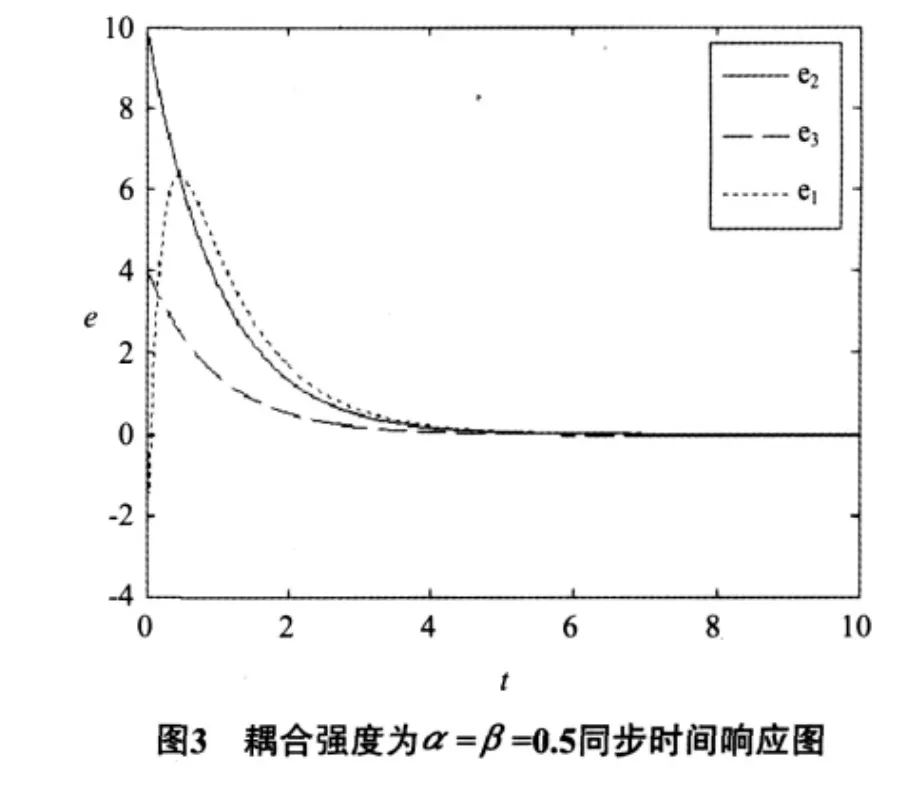
考虑Chu系统的对称的非线性耦合同步，即取耦合强度α=β讨论Chu系统的混沌同步，当α=β=0.5时，同步误差系统(11)的Jacobi矩阵的特征值为(－5，－1，－1)均为负实数，满足线性系统稳定性准则，其同步误差具有渐进稳定性，并不用计算Lyapunov指数.取初值为［－5，－7，5，3，－3，9，－3，10，4］，图3 给出了耦合强度为α=β=0.5时的同步结果，图3的模拟结果表明2个混沌Chu系统(9)和(10)迅速能实现混沌同步.

在对称耦合α=β的情况下，通过数值模拟可以得到同步误差的最大Lyapunov指数与耦合强度之间的关系图，当同步误差的最大Lyapunov指数为负值时，可以实现系统状态的完全同步，混沌同步状态是稳定的，从而可以得到满足同步稳定性要求的耦合强度α，β的范围.

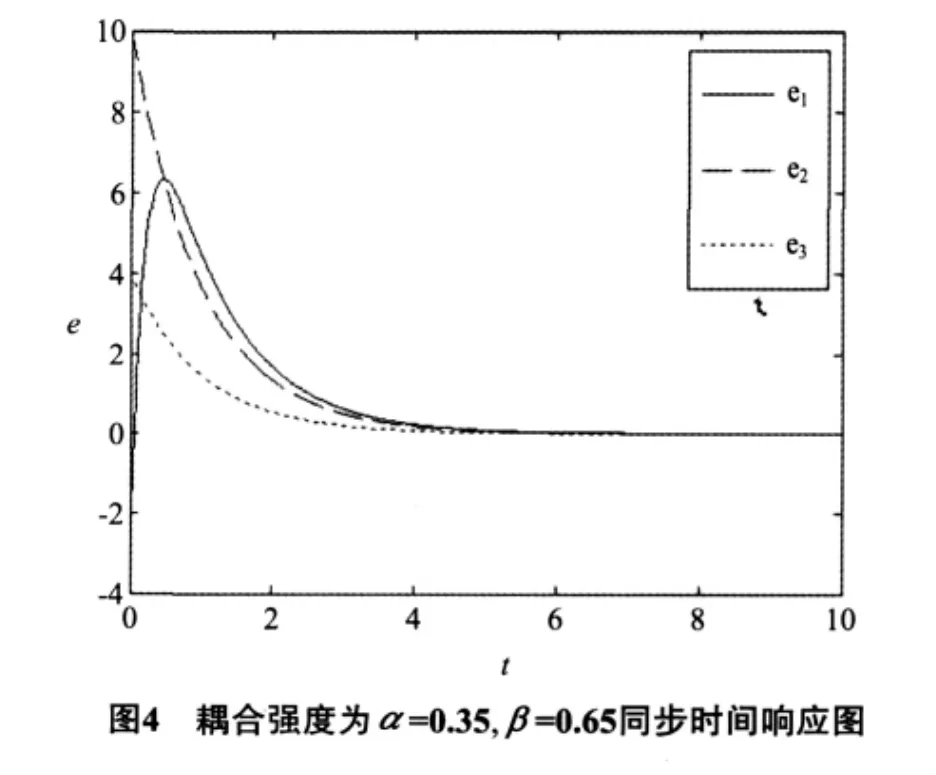
对于非对称的非线性耦合同步，即取耦合强度α≠β，当 α+β=1时，同步误差系统(11)的Jacobi矩阵的特征值仍为(－5，－1，－1)且均为负实数，满足线性系统稳定性准则，其同步误差具有渐进稳定性，并不用计算Lyapunov指数.图4给出了耦合强度分别为α=0.35，β=0.65时的同步结果，图4的模拟结果表明2个混沌Chu系统(9)和(10)迅速能实现混沌同步.

3 结论

本文利用对称非线性耦合混沌同步的方法，研究了一个新的混沌系统:Chu系统的混沌同步，讨论了该系统在不同耦合强度α，β的作用下，2个混沌系统存在的混沌同步现象，数值模拟显示当参数α+β=1时，参数α，β对同步的稳定性影响不大，证实了该混沌同步方法的有效性.

［1］陈关荣，吕金虎.Lorenz系统族的动力学分析、控制与同步［M］.北京:科学出版社，2003.

［2］陆启韶.分岔与奇异性［M］.上海:上海科技教育出版社，1995.

［3］刘秉正，彭建华.非线性动力学［M］.北京:高等教育出版社，2004.

［4］PECORA L M，CARROLL T L.Synchronization in chaotic systems［J］.Physical Review Letters，1990 ，64(8):821－824.

［5］LORENZ E N.Deteeministic nonperiodic flow［J］.Journal of the Atmospheric Sciences，1963，20(2):130 －141.

［6］黄润生，黄洁.混沌及其应用［M］.武汉:武汉大学出版社，2005.

［7］于洪洁，刘延柱.对称非线性耦合混沌系统的同步［J］.物理学报，2005，54(7):3 029 －3 033.

［8］于洪洁，郑宁.非线性函数耦合的Chen吸引子网络的混沌同步［J］.物理学报，2008，57(8):4 712－4 720.

［9］楮衍东，李险峰，张建刚，等.一类新自治混沌系统的计算机仿真与电路模拟［J］.四川大学学报:自然科学版，2007，44(3):596－602.

［10］李响，张荣，潘正华.一类混沌系统的混沌同步［J］.江南大学学报:自然科学版，2009，8(2):238－241.

(责任编辑梁志茂)

Nonlinear Coupling Synchronization of a New Chaotic System

ZHANG Xu-dong1，YU Jian-ning1，GUO Lan-ping1，PENG Jian-kui2，ZHANG Jian-gang1
(1.School of Mathematics，Physics and Software Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China;2.School of Mathematics and Information Engineering，Gansu Lianhe University，Lanzhou 730000，China)

This paper discusses the nonlinear characteristics of a new chaotic system，and gives the phase diagram of the system，power spectrum，Poincare mapping and Lyapunov index.It uses the nonlinear function coupling method to discuss the chaotic synchronization problems of the chaotic attractor.Through the numerical simulation it is concluded that the initial value and the choice of the coupling strength factor has less influence on the realization of chaos synchronization，which has proved that this chaotic synchronization method is effective.

new chaotic system;nonlinear coupling;Poincare mapping;Lyapunov index spectrum

O 322

A

1672－8513(2011)02－0149－03

10.3969/j.issn.1672 －8513.2011.02.018

2010－11－04.

国家自然科学基金(408034);甘肃省自然科学基金(3ZS051－A25－030，3ZS－042－B25－049);兰州交通大学科研基金(DXS2010－018)

张旭东(1984－)，男，硕士研究生.主要研究方向:非线性动力系统.

俞建宁(1957－)，男，教授，博士生导师.主要研究方向:非线性动力系统.