生成函数在稳定常数测定中的应用

2011-09-26张云房淑宁余珍张良

大学化学 2011年3期

张云房淑宁余珍张良

(同济大学化学系上海 200092)

1941年,Bjerrum提出了生成函数(也被称作Bjerrum函数)的概念[1-2]。生成函数既适用于配位反应体系[3-4],也适用于酸碱反应体系[5-6]。利用生成函数测定配合物或酸稳定常数的方法,称作生成函数法。根据数据处理方式的不同,生成函数法可以分为直接计算法、分段拟合法及半整数法。生成函数法有下述好处：其一,涉及配合物或酸稳定常数测定的计算模型通常是非线性关系式,这类计算模型一般需要使用求解非线性问题的计算方法。生成函数法将这类计算模型转化为线性关系式,仅需使用求解线性问题的计算方法(如线性最小二乘法),从而简化了计算过程。其二,配合物稳定常数测定的计算模型与酸稳定常数测定的计算模型是不同的,生成函数法在形式上统一了这两类计算模型,而且测定的基本方法也是相同的。其三,生成函数法的检测,可以用电位法,也可以用其他方法(如光度法等),但无论使用何种检测手段,计算模型是不变的。其四,生成函数法属于线性滴定法[7-8],生成函数法的计算模型可以从线性滴定法的计算模型导出。本文介绍了生成函数法的分类、基本原理、测定方法、各种方法的特点及应用实例。

1 生成函数法的有关概念

1.1 生成函数的定义

(1)

配合物生成函数的物理意义是,在一定电位(或配位剂平衡浓度)条件下,与金属离子配合的平均配位剂数。因此,配合物的生成函数也被称作平均配位数。

(2)

酸的质子化生成函数的物理意义是,在一定电位(或pH)条件下,与酸根结合的平均质子数。因此,酸的质子化生成函数也被称作平均质子数。

(3)

利用式(3),可以对配合物(或酸)的稳定常数进行测定。

1.2 生成函数与滴定剂体积及配位剂(或氢离子)浓度的关系

(4)

需要强调的是,生成函数与滴定剂体积及配位剂(或氢离子)浓度的关系往往与反应体系的性质有关；不同体系的生成函数与滴定剂体积及配位剂(或氢离子)浓度的关系通常是不同的。如：①氟-铝配位反应体系,当用氟离子标准溶液滴定铝离子溶液时,式(4)可以写作[3]：

(5)

式(5)中,c和cF是铝离子和氟离子的分析浓度,V0是铝离子溶液的初始体积,V和[F-]分别是加入的氟离子溶液的体积和氟离子的平衡浓度；②中性氨基酸(如甘氨酸、丝氨酸及蛋氨酸等)-铜配位反应体系,当用标准碱溶液滴定由中性氨基酸与铜离子构成的混合溶液时,式(4)可以写作[4]:

(6)

式(6)中,cB和cCu是标准碱和铜离子的分析浓度,V0是混合溶液的初始体积,V是加入的标准碱溶液的体积；③酸碱反应体系,当用标准碱溶液滴定酸溶液时,式(4)可以写作[5]:

(7)

式(7)中,n是酸的元数,Kw是水的质子自递常数,c和cB是酸和标准碱的分析浓度,V0是酸溶液的初始体积,V和[H+]是加入的标准碱溶液的体积和相应的氢离子浓度。

1.3 配位剂(或氢离子)平衡浓度的测定方法

由于检测手段不同,配位剂(或氢离子)平衡浓度的测定方法可以分为两类。第一类,直接测定游离配位剂(或氢离子)的平衡浓度。如氟-金属离子配合物稳定常数的测定,可以用氟离子选择性电极直接测定游离氟离子的平衡浓度[3]；又如酸稳定常数的测定,可以用氢离子选择性电极直接测定游离氢离子的平衡浓度[4]。这类配位剂(或氢离子)平衡浓度的测定方法比较简单。第二类,间接测定游离配位剂的平衡浓度。如中性氨基酸-铜配合物稳定常数的测定,由于直接测定中性氨基酸根离子的平衡浓度有一定困难,可以在标准碱溶液滴定由中性氨基酸与铜离子构成的混合溶液的过程中，通过测定氢离子浓度的变化,间接求出中性氨基酸根离子的平衡浓度。此时,配位剂(即中性氨基酸根离子)的平衡浓度[L]可以表示为[4]：

(8)

式(8)中的cHL和cB是中性氨基酸和标准碱的分析浓度,V0是中性氨基酸和铜离子构成的混合溶液的初始体积,V和[H+]是加入的标准碱溶液的体积和相应的氢离子浓度,Ka是中性氨基酸偶极离子的离解常数(中性氨基酸在水溶液中一般以正离子、偶极离子及负离子等3种形式存在[9],但在本例条件下,正离子的浓度接近于0,所以仅需考虑偶极离子的离解)。由于涉及配位剂离子(如中性氨基酸根离子)、金属离子(如铜离子)及氢离子之间的多重平衡,这类配位剂平衡浓度的测定一般比第一类复杂。

2 生成函数法的分类及原理

2.1 直接计算生成函数法

将式(3)写作以下形式,可以得到生成函数法测定配合物(或酸)稳定常数的基本关系式：

(9)

求出βj后,若还需求出配合物(或酸)的各级稳定常数Kj(j=1,2,…,n),则按下式计算：

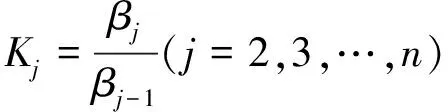
(10)

2.2 分段拟合生成函数法

曲线拟合常用的函数形式是指数函数和幂函数[6],也可以采用多项式拟合的形式。

2.3 半整数生成函数法

βj-1[L]j-1=βj[L]j或βj-1[H+]j-1=βj[H+]j

(11)

根据累积稳定常数βj与稳定常数Kj的关系,式(11)可以写作:

lgKj=-lg[L] 或 lgKj=-lg[H+]

(12)

应该注意的是,半整数生成函数法是一种近似计算方法,这种方法的使用条件是第j-1级配合位(或酸)与第j级配合位(或酸)的分布系数相等,并且均为0.5,这个条件只有在配合位(或酸)各级稳定常数的差值ΔK足够大的情况下才能满足[8]。

3 生成函数法的特点

3.1 数据采集的位置

3.2 分段拟合生成函数法及半整数生成函数法对稳定常数大小的要求

3.3 各种生成函数法的特点

4 应用实例

4.1 测定对象及结果

作为应用实例,利用各种生成函数法对丝氨酸-铜配合物、蛋氨酸-铜配合物、丁二酸及酒石酸的条件稳定常数进行了测定(结果见表1,测定步骤及数据处理见后续)。其中,分段拟合法所用的拟合函数是指数函数：

(13)

此外,文献[4-6]也介绍了生成函数法对配合物或酸稳定常数测定的实例。

表1 各种生成函数法对中性氨基酸-铜配合物及多元酸条件稳定常数的测定结果(n=3)

4.2 测定步骤

用0.08376mol/L NaOH溶液滴定50mL由0.01000mol/L丝氨酸(或蛋氨酸)与0.001993mol/L硫酸铜构成的混合溶液；或用0.09289mol/L NaOH溶液滴定50mL 0.009429mol/L丁二酸(或0.009089mol/L酒石酸)溶液,测出一系列滴定数据V和E。测定所用的仪器为798MPT全自动电位滴定仪及氢离子选择性复合电极(瑞士万通公司生产)；待测溶液含0.1mol/L氯化钾作为离子强度调节剂；滴定步长0.10mL。

4.3 电极的校正

溶液的氢离子浓度[H+]与氢离子选择性复合电极的电位(或由氢离子选择性电极与参比电极构成的工作电池的电动势)E的关系为：

[H+]=f×10(E-K)/S

(14)

式(14)中,f是氢离子浓度的校正系数(活度系数的倒数),在实际测定中,可以假设其近似为1。在实验温度及离子强度一定的条件下,K和S是常数,可以用pH为4.00、6.86及9.18(均25℃)的3种标准缓冲溶液(成套试剂)测出；实验测出溶液的E,按式(14)求出相应的[H+]。应该注意的是,在此基础上测出的稳定常数,并非严格意义的热力学稳定常数,而仅仅是条件稳定常数。