一类带移民的二次加权分枝模型

张红霞，李俊平

1 模型建立

马尔可夫过程是一类极为重要的随机过程，是解决存储问题、排队问题、人口问题、风险问题等等的有效的数学工具。而马尔可夫分枝过程又是马尔可夫过程的重要分支，在排队论、生物学、物理学等等中具有非常广泛的应用。经典马尔可夫分枝过程已得到广泛研究，它的最基本的性质就是分枝性，直观的说，分枝性就是系统中不同粒子之间是相互独立、互不干扰的。然而，在大多数现实情况中，不同粒子之间往往不是相互独立的，而是密切相关的，因此很多学者对经典马尔可夫分枝模型进行了多种形式的推广。如Pakes和Tavare[1]、Li.J.P和Chen.A.Y.[2,3]等等.本文是在前人工作的基础上推广了模型，同样具有相当重要的研究意义。

针对于移民状态下，建立以下分枝模型：

定义 1.1 一个 q-矩阵 Q={qij;  i,j ∈ Z+}被称为 QWBI-q-矩阵,如果

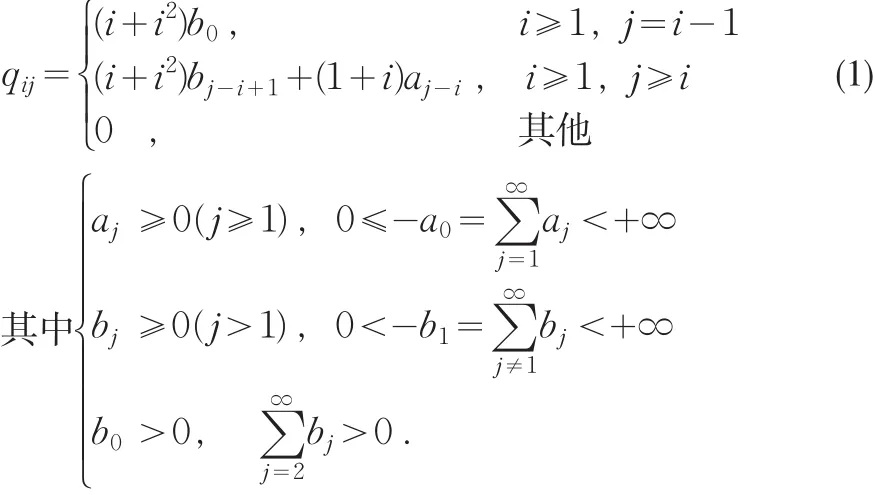
在本文中，Z+={ }0, 1, 2… ，QWBI-q-矩阵：带移民的二次加权q-矩阵；QWMBPI：带移民的二次加权马尔可夫分枝过程

定义1.2一个QWMBPI就是一个Z+-值的连续时间参数的马尔可夫链,其转移函数P(t)={pij()t;  i,j∈ Z+} 满 足Kolmogorov向前方程：P'(t)=P(t)Q且Q形如(1.1).

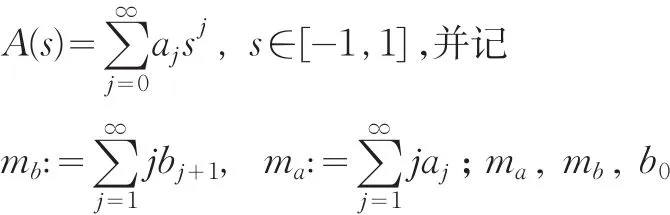
分别表示平均出生率,移入率,死亡率。

2 吸收概率

设   {X(t); t≥ 0} 是给定的 WBI-q-矩阵 Q 的(唯一的)WMBPI,显然0为吸收状态.

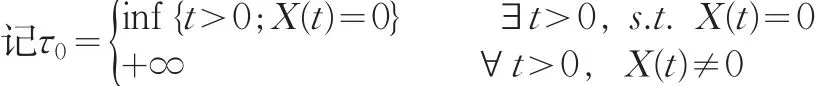
为   {X(t); t≥ 0}的吸收时刻,对 ∀i≥ 1,有pi(τ0＜∞)表示粒子从状态i出发,而被吸收的概率,即到达状态0的概率。由[4]及式(1)易知状态集{1,2,…}构成一个连通类,所以对∀i≥1,要么ai0=1,要么ai0＜1.

由文献[1,5]易知下面的引理2.1成立.

x*i=qi0=0(0 ≤ xj≤ 1 , i ≥ 1)的最小解.

下面的定理2.2.利用引理2.1得到了吸收概率ai0=1(∀i≥1)的充分必要条件以及在三种情况下的表达式。

定理2.1记s0为方程 B(s)+s A(s)=0在[0,1]内的最小根，q为方程B(s)=0在[0,1]内的最小根，若定义

对∀i≥1,ai0=1当且仅当mb≤b0,J=+∞

而且

①若mb≤b0,J=+∞,则对∀i≥1，有

②若mb≤b0,J＜+∞,则对∀i≥1，有

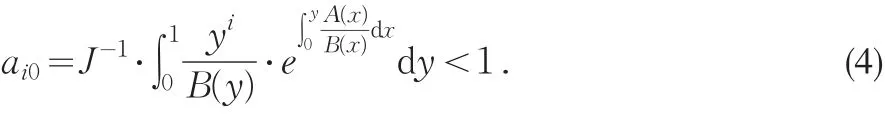
③若b0≤mb≤+∞,则对∀i≥1，有

证明对∀i≥1,令

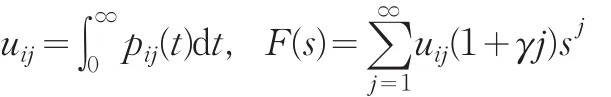
由[6](4)知：F(s)＜∞,由[7]和[6]知,对 ∀s∈[ )0 ,1 ，有

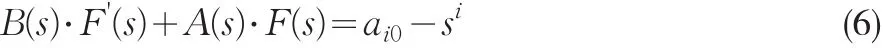
当mb≤b0,J=+∞时,对∀s∈[ )0 ,1, i≥ 1,解(6)得：

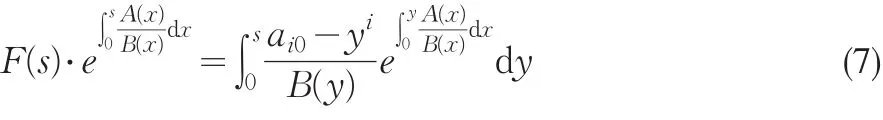
当 J=+∞时,必有ai0=1,否则若ai0＜1,则在(7)两端令s↑1,右端趋于-∞,而左端非负,因此矛盾。

当mb≤b0,J＜+∞时,由 J的定义知,当 J＜+∞时有,对 ∀s∈i≥ 1,由(7)知

在(8)中令 s↑1,得,

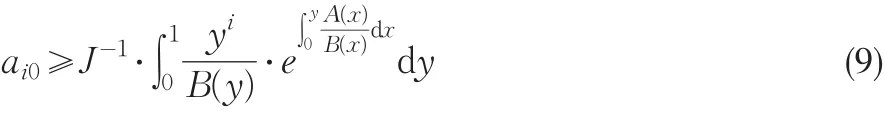
则对 ∀i≥1,有,

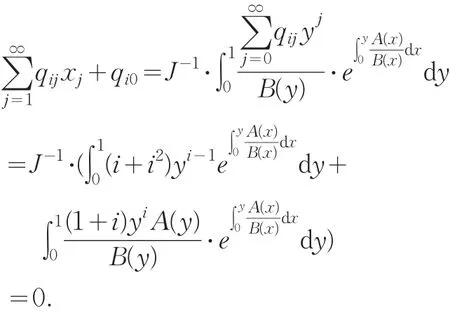
因此由引理 2.1 知：ai0≤ xi(i≥ 1).

当b0＜mb≤+∞时,易知,

(mb-b0)+ma＞0,0＜s0＜q＜1.由[7]知：

在(10)中令 s=q,则

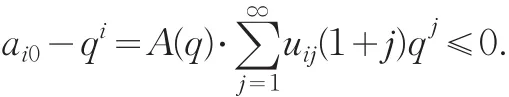
因 此 ai0≤qi＜1,且 ai0=qi当 且 仅 当 a0=0.对∀s∈(q,1)有

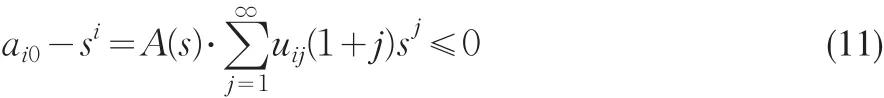
所以ai0≤qi.对∀s∈[ )0 ,s0

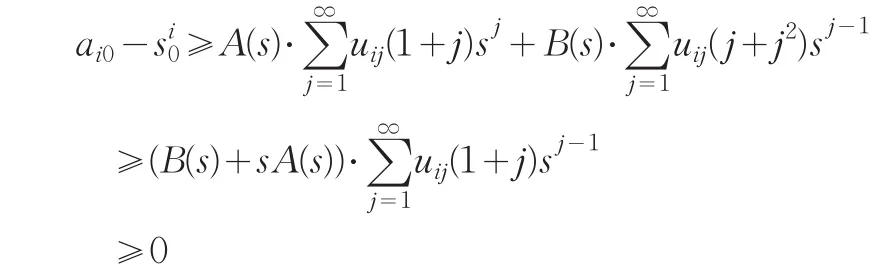
所以ai0≥si0.因此 si0≤ai0≤qi＜1.

综上所述,对 ∀ i≥1,ai0=1当且仅当 mb͂≤b0,J=+∞ .

本文讨论的这类分枝模型.得到了马尔可夫分枝过程在状态0的吸收概率的表达式，对研究一些现象如生物繁殖、细胞癌变、原子分裂等等有重要的意义。

[1]Pakes A.G.Expiosive Markov Branching Processes[J]:Entrance Laws and Limiting Behavior[J].Adv.Appl.Prob.,1993,25.

[2]Chen A.Y.,Li J.P.,Remesh N.I.Uniqueness and Hitting Time of Weighted Markov bran-ching Processes[J].Methodology and Compu-tingin Applied Probability,2005,7.

[3]Li J.P.Markov Branching Processwith I-mmigration and Resurrection[J].Markov Pro-cessesand Related Fields,2006,12.

[4]Anderson W.J.Continuous-Time Markov Chains[M].Berlin:Springer,1990.

[5]Pakes A.G.Absorbing Markov Branching Processes with a State-dependent Immigration[J].Adv.Proc.Appl.,1993,（48）.

[6]张红霞,李树君,一类带移民的加权分枝过程的有关结论[J].黑龙江科技信息,2010,（37）.

[7]张红霞,李树君,一类带移民的二次加权马尔可夫分枝过程[J].科技经济市场,2010,（3）.