企业违规行为区域化、反复化的成因与治理

秦永恒，万迪日方

0 引言

企业违规行为是商业企业采取违法手段谋求不正当利益的行为。由于高额非法收益的存在，企业违规行为是一种长期和普遍的存在，这不仅增加了监管部门的工作难度，更损害了广大消费群体的根本利益。近期，一些企业的违规行为更是屡屡见诸媒体报端，综而观之，这类行为多呈现出两种特点，一种是违规的区域化，也就是同一个区域内有多家企业采取同样的违规手段牟利，如河北昌黎多家企业生产假葡萄酒低价销售，北京、甘肃等地的许多销售商大量采用填充水泥的包装箱用于苹果整箱销售等；另一种就是违规的反复化，企业的违规屡查屡犯，屡禁不止，如安徽血铅事件中的当事企业就曾多次整改，但仍然对环境造成了严重污染，并危及了当地居民的生命安全。

这些事件的发生，除了企业方面的逐利因素，相关的监管检查的不力或缺失也是其发生的一个重要原因，这可以看作是企业利益和监管检查两个因素交互之下的结果。对两者关系的相关研究中，葛和平与曹家和就曾从静态博弈的角度对外资并购中国上市公司过程中的违规与监管进行了分析[1]，吴桐与徐荣贞则从演化博弈的角度对金融创新与外部监管进行了探讨[2]。但在分析原因并提出相应的政策改进建议之外，更为重要的是在违规发生后，应该如何采取有力措施在短时间内予以应对并防止他们的再次发生，这是在已有研究中所缺少的。

针对以上问题，本文首先从动态学习的角度分析了企业违规行为在监管存在的条件下扩散或反复的原因和过程，因为与传统的非合作博弈理论认为均衡是在博弈的规则、参与人的理性以及参与人的支付都是共同知识的条件下由参与人的分析和自省所得出的结果不同，演化博弈理论认为均衡是并非完全理性的参与人随着时间的推移寻求最优化这一过程的长期结果[3]，这使得该理论的应用更加切合实际，而将参与者的学习过程引入演化博弈则能使之更好的应用于社会经济演化的分析之中[4]。进一步地，本文从微分动力系统的最优控制角度分析了违规行为发生之后的应对思路，并提出了对监管部门的措施建议。

1 基本模型

违规企业与行政监管部门在目标上是存在根本对立的。借鉴Mostagir提出的委托-代理博弈模型[5]，本文将以上双方的博弈模型化，如表1所示。其中行所在博弈方为企业，列所在博弈方为监管部门。企业方可以为同一区域内的全部同类企业，x(t)为其中采取违规策略的企业比例，其值是时间的函数，表示其随时间的动态变化；或者企业方也可以为某个单一主体，x(t)则表示其采取违规策略的概率。行政监管部门为单一主体，其采取监管策略的概率为u(t)，如果企业方为多个企业时，u(t)则表示其中被加以监管检查的企业比例。

当企业依法进行生产销售时，行政部门的监管与否不会对其收益造成显著影响，此时企业的收益为V1，当企业违规操作时，遭遇监管检查将使其违法获得收益，而监管部门的失察或放任则会导致其获得更高的违法收益V2，由企业方收益的实际含义可知0＜V1＜V2。而监管部门方考虑的显然并非收益，而是监管成本或公众利益的损失：当对诚信的企业进行监管时，全面的检查也不会获得实质性发现，此时付出的监管成本为C2，而对违规企业的监管要么可以轻易发现，要么虽然发现难度较高，但发现后所能避免或挽回的经济损失必然更高，因此此时付出的总体监管成本较低，为C1，如果行政部门采取放任态度，对于诚信的企业，他们付出的监管成本为0，而对违规企业的放任将导致巨大的社会危害或经济损失，因此此时的不作为是以更高的成本C3为代价的。因此，监管部门的成本有如下关系：0＜C1＜C2＜C3。 在 这 种 设 定下，博弈不存在纯策略纳什均衡，并且违规的最高收益对应于监管部门的最高成本，暗示出双方目标的根本对立。

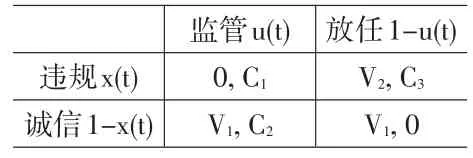
表1 企业与行政监管博弈的得益矩阵

设初始状态下存在较低比例的违规企业，因而有0＜x(0)＜1，同时，监管部门一般也采取的是抽查的监管方式，因而有0＜u(0)＜1。企业策略的选择一部分是自主完成，而更大部分则是通过对其他企业策略的动态学习。企业在每个阶段随机两两匹配，学习过程遵循强化学习模式[6]。当一方看到另一方由于采取不同于己方策略得到了更高的收益，则会以一定比例模仿另一方，在后续阶段也采取对方的策略，而如果看到对方的策略相同或者与己不同但得到了低于己方当前策略的收益，则不会调整。因此，根据学习过程并结合得益矩阵，可以知道企业策略的转变只会发生在两种情况下：或是受到监管检查的情况下违规企业因观察到诚信企业的做法可以获利而向诚信策略转变，或是不存在监管检查的情况下诚信企业因观察到违规企业获利更高而冒险向违规策略转变。那么，处于监管条件下的违规企业比例为x(t)u(t),他们遇到违规企业的概率为1-x(t)，因此第一种情况发生的比例为x(t)u(t)(1-x(t))，同理，第二种情况发生的比例为(1-x(t))(1-u(t))x(t)。另外，考虑到并非所有的企业都会转变或者立即进行转变，因此设第一种情况下企业改变策略的概率为p,第二种情况下企业改变策略的概率为q，则两种情况下策略转变的比例分别为 px(t)u(t)(1-x(t))和q(1-x(t))(1-u(t))x(t)。于是，在连续时间情形下，系统动态可以表示为：

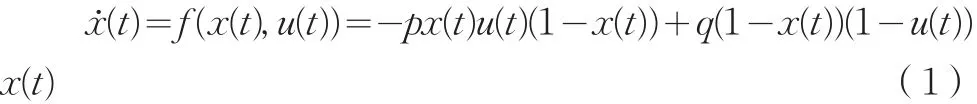
省略时间标记t，并对上式化简，得到

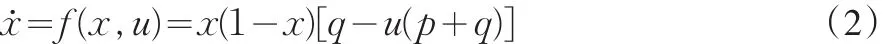
以上的分析同样适用于单一企业违规行为的情形，其差别仅仅在于由多个企业间的横向学习变为了自身之间的纵向学习。初始阶段企业可能存在较低概率的违规行为，当遭遇监管检查时，会向自身之前的合法经营方式转变，而未遇到检查时，则会以一定比例向追求更多非法收益的方式转变。另外，本文中所提及的监管检查必须是实质性的检查，而非流于形式的表面工作。

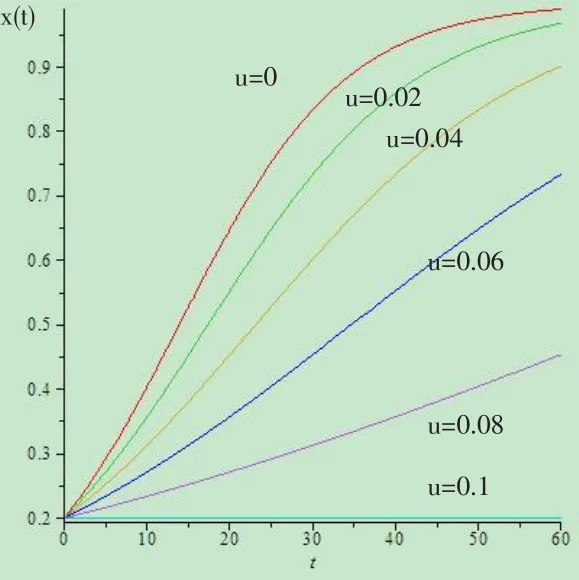
图1 监管检查力度较低时x(t)的变化曲线

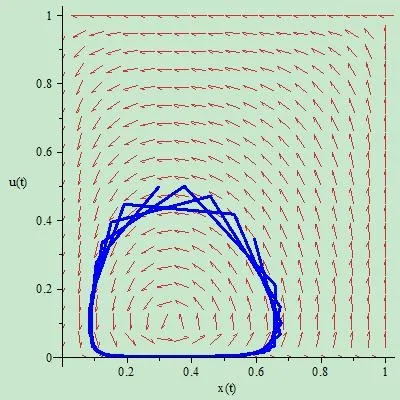
图2 监管检查力度内生动态变化时的系统相图

2 违规行为的区域化和反复化

2.1 违规行为区域化成因分析

当相应的监管检查缺失或力度不足时，违规行为面临的风险较低而获利较高，因此会鼓励更多企业通过效仿参与其中，并进而导致违规企业在某地域内的比例升高，形成违规行为的区域化。从（2）式来看，考虑到0＜x(t)＜1，因此当 q-u(t)(p+q)＞0，也即 u(t)＜时，x·(t)＞0，违规企业的比例将逐渐增加。取p=0.9和q=0.1,这表示违规企业遭遇检查时多数会立即纠正错误，转为正规生产经营，而企业对采取违规行为相对谨慎，转变比例较低。对(2)式进行数值仿真，得到如所示的结果。可以看到，当监管水平较低时，违规企业的比例依然可以在短时间内可以达到很高比例，因此现有监管水平的高低是违规行为区域化的重要形成原因。

2.2 违规行为反复化成因分析

如果行政监管的力度由系统内生确定，即监管部门处于监管成本的考虑，也会对监管力度进行动态调整，因为当区域内企业违规比例较低时，全面密集的检查会导致高昂的监督成本，而且检查结果也并不会因此而显著改变。假设监管部门的监管力度调整也遵循动态学习的规则，策略的调整包含两种情况，一种是对现有违规企业由放任转为监管，另一种则是对现有诚信企业放松监管，并设相应的策略转变概率分别为r和s，当r=1时即表示对违规企业立即采取措施，绝不放任，而s＞0则表示监管部门对诚信企业的检查放松程度。根据与之前类似的分析，可得连续时间状态下监管比例的动态方程为：

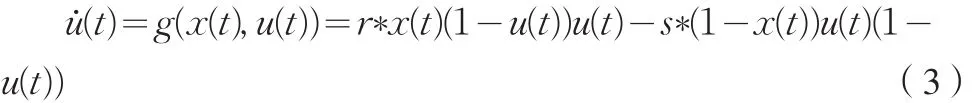
省略时间标记t并化简得：

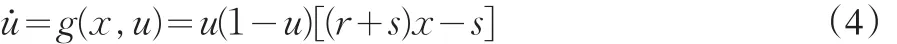
此时的系统动态由（2）和（4）式联立构成的微分方程组描述。

对由（2）和（4）构成的非线性微分方程组在均衡点的邻域内线性化展开，得

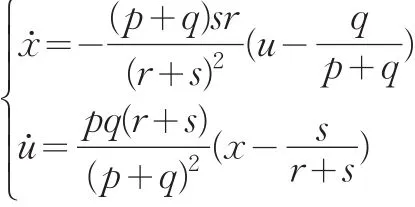
取p=0.9,q=0.1,r=1,s=0.5,x(0)=0.3,u(0)=0.5,绘制动态系统的轨线和向量场，如图2所示。由图像可以看到，在监管力度动态调整的情况下，企业违规行为的比例（或单一企业违规行为的概率）将根据监管力度相应调整。当比例达到一定水平之后，监管力度也随之提高，并使得违规比例相应下降，在下降到某一水平之后，监管力度也会随之下降，并导致以后违规行为的死灰复燃。违规与监管在长期内形成一个交替升降的循环过程。由此可知，监管检查力度随违规水平的动态调整是导致违规行为反复化的重要原因。而违规行为的平均水平，即均衡点的位置，由动态学习的行为转化概率决定，违规行为的峰值则由采取监管检查行动时的既有监管水平和违规水平，即系统的初始状态决定。

3 企业违规行为的监管应对建议

3.1 短期内迅速降低

要达到迅速降低违规水平的目标，即是要使由式（2）确定的动力系统归零的时间最短。这构成了系统的最短时间控制问题，相应的的性能泛函为：

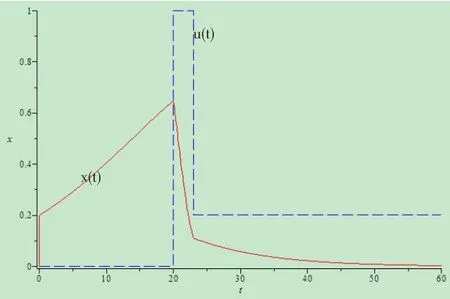
图3 监管检查力度外生动态调整时x(t)的变化曲线

J=∫0tfd t，其中tf为控制的终端时间，控制变量受约束0≤u(t)≤1。

构造Hamilton函数，得：

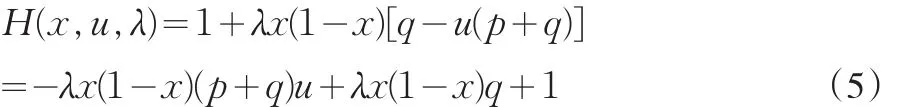
注意到式（5）中Hamilton函数关于u是线性的，且由实际意义可知,p＞0,q≥0，以及x(0)＞0，所以得到系统的最优控制为：

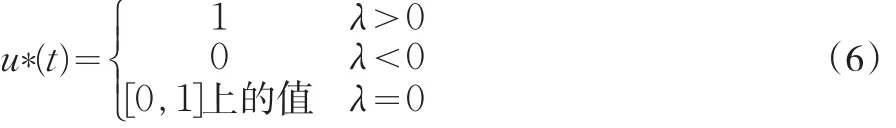
其中的Hamilton乘子λ(t)表示在t时刻状态变量x(t)的边际效应，在本文所述问题中的实际含义为欺诈企业比例增加所导致的消除时间的增加量。因此，式（6）的最优控制表明，只要违规比例的提高会导致控制过程的时间延长，则为了尽快消除这种行为，就应该对区域内的所有企业采取无差别的全面检查（对单一企业则意味着对其进行连续全面的跟踪）。

3.2 长期内控制并消除

要在长期内控制某一违规现象的比例并最终消除这种现象，就意味着要使由式（2）所确定的动力系统的演化稳定均衡为x=0。由式（2）得：

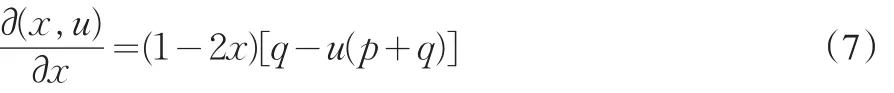
式（8）的结果表明，若要达到长期内控制违规行为水平并最终消除的目标，就要使监管检查的力度保持于某一水平之上，该水平亦由动态学习的行为转化概率确定。同时，考虑到监管检查成本的因素，因此只要使监管力度常态化，并略高于必要水平即可，即令u为略大于的常数。

取p=0.9,q=0.1,x(0)=0.2,u(0)=0,u(20)=1,u(23)=0.2，动态系统的变化趋势如图3所示。可以看到，当某种违规行为凸显时，只要迅速采取全面或连续的监管检查，就可以在短时间内（t=3）使违规行为的水平快速降低；当违规行为的蔓延势头得到遏制并降低到较低水平后，就可以将监管检查的力度也降低到略高于必要水平，并且当这种力度在长期期稳定保持下去时，企业的同类违规行为将进一步降低并最终消除。

4 结论

本文针对企业与监管部门间的博弈关系，构建了基于动态学习的企业违规行为微分动力系统。并在此基础上分析了近一段时间媒体报道中频繁出现的企业违规行为区域化、反复化现象，指出监管检查力度的不足和动态调整是导致以上现象出现的重要原因。并从最优控制和演化稳定策略的角度分析了以上现象出现后的应对措施，提出应在短时间内采取普查的方式迅速降低违规行为的比例（或概率），并在较长长期内保持必要的监管力度以进一步降低其比例并最终达到消除该类违规行为的目标。

本文的结论适用于对不同类型企业如生产型、销售型企业行为的监管，对于不同类型的行业监管如食品卫生监督、金融监管等同样具有参考价值。在尚无针对某一违规行为的专门应对措施（比如针对水泥苹果包装箱的销售实名制）或该措施出台之前，本文提出的对监管检查力度的调整建议将可以作为一般性的应对举措加以实施。

另外需要指出的是，文中的分析是在监管成本有限的隐含假设下得出的。对于现实中某些违规行为监管检查难度极大或者监管成本极高的情形，要么u(t)所受到约束的上限将小于1，要么相应的控制措施项中还须包含对成本项的考虑，导致此时采取u(t)=1的控制方式的阈值会适当提高，但无论如何，对违规行为采取砰-砰控制（Bang-bang Control）的思想是确定不变的。

[1]葛和平，曹家和.外资并购中国上市公司中违规与监管的博弈分析[J].统计与决策.2006,(14).

[2]吴桐，徐荣贞.金融危机下金融创新与监管的演化博弈分析[J].统计与决策.2010,(18).

[3]Fudenberg D,Levine D K.The Theory of Learning in Games[M].Cambridge:The MITPress,1998.

[4]黄凯南.演化博弈与演化经济学[J].经济研究.2009,(02).

[5]Mostagir M.Exploiting Myopic Learning:INFORMSAnnual Meeting[Z].Austin,Texas:2010.

[6]Borgers T,Sarin R.Learning Through Reinforcement and Replicator Dynamics[J].Journal of Economic Theory,1997,77(1).

[7]马知恩，周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.