考虑资产价格波动的前瞻性泰勒规则及实证检验

李 涛，傅 强

0 前言

货币政策是否对资产价格作出反应一直是学术界争论的焦点。第一种观点认为资产价格不应成为货币政策目标，货币政策实际上也无法改变影响资产价格的长期利率环境。若将资产价格列人货币政策目标，无疑会增加货币政策实施的难度，中央银行的占优选择是所谓“事后救助”策略(“mop up after”strategy)，即通过及时注入充足流动性来缓解资产泡沫破裂对经济形成的冲击。另一种理念则认为货币政策应当关注资产价格变动。欧央行认为，资产泡沫膨胀一般来说都与货币信贷的高增长相伴随，尤其是在经济上升期及住房等资产价格膨胀的阶段。中央银行要加强对货币信贷的监测分析，对资产价格波动中反映的未来通胀信息应给予关注，构建了资产价格变化与货币政策的反应关系。西方国家操作货币政策的理论依据是泰勒规则。它假定货币当局运用货币政策工具围绕两大关键目标函数，即实际通货膨胀率和目标通货膨胀率之间的偏离程度(通胀缺口)以及实际产出水平和潜在产出水平之间的偏离程度(产出缺口)（Taylor，1993）][1]。泰勒规则提出之后，许多学者对其进行了修正以完善货币政策调控框架：①引人利率平滑行为(Or-phanides,2001)[2]。②加入前瞻性变量（CGG,2000)[3]。③修正产出缺口以降低潜在产出的测量误差(Orphanides,2003)[4]。④引人资产价格、汇率等其他重要变量(Siklos,Wemer&Bohl,2004[5];Ball,1999[6];Svensson,2000[7]等)。

泰勒规则在我国货币政策运用是否考虑资产价格因素是一个值得研究的问题。我国股市诞生之日起，股票价格暴涨暴跌虽已屡见不鲜，资产价格泡沫已经是不争的事实，直接危及金融安全与经济发展。这对我国央行制定有效货币政策，保持经济与社会平稳发展，具有重要的理论与现实意义。本文在借鉴国外研究的基础上，结合中国国情对泰勒规则进行合理扩展，最终构建把资产价格纳入框架的货币政策利率反应模型，并基于2000～2009年经济金融数据进行实证检验，最后提出相关对策建议。

1 考虑资产价格的前瞻性泰勒规则模型

泰勒（1993）将中央银行的利率调控规则设定为：

其中，it是联邦基金利率，πat是前四季度的平均通胀率，y͂t是产出缺口，y͂t=100（y-y*）/y*，y 是真实GDP，y*是潜在GDP。

Clarida，Gali和Gertler(1997，2000)认为鉴于货币政策的前瞻性特点，使短期利率成为通货膨胀预期缺口和产出缺口的函数，能够更真实地反映央行的实际决策过程以及更好地适应货币政策作用的时滞。假定短期名义利率根据产出缺口和通胀缺口进行调整，即用以下方程表示短期名义利率的变化:

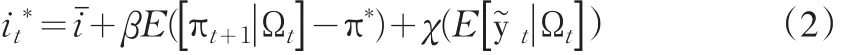
其中it*表示在t期货币政策的目标利率，iˉ表示长期均衡名义利率，πt+n表示从t期到t+n期价格水平变化的百分比，π*表示通胀目标，y͂t是t期的产出缺口，E是预期因子,Ωt表示在t期利率制定时的信息集。

Hans Genberg（2001）[15]和 Siklos，Werner&Bohl(2004)的研究表明资产价格包含了未来总需求及其引起的通胀压力的重要信息，资产价格波动对货币政策传导具有一定的内生性。泰勒模型中加入资产价格可以提高货币政策的有效性。本文借鉴Siklos，Werner&Bohl(2004)的研究，以股票市场总市值作为资产价格的代理变量加入泰勒规则。则（2）式变为

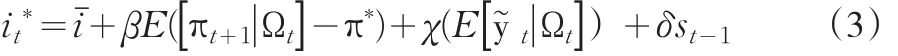
其中，St-1为之后一期资产价格。

Or-phanides(2001)认为在泰勒规则内引人利率平滑（interest rate smoothing），较之原泰勒规则能够更好地符合实际观察到的政策。利率平滑现象是指货币当局为维护信誉，并不是将利率一步调整至目标利率，而是逐步将利率调整至目标水平，具体表现为以同一方向上连续微幅调整利率而逆向变化频率低间隔时间长。

假定中央银行调整利率有平滑行为，以下面的式子描述:

其中参数ρ∈(0,1)，反映平滑调整的程度，vt是零均值关于利率外在冲击的随机扰动项，it是货币当局设定的当前利率水平。

将（4）代入（3），

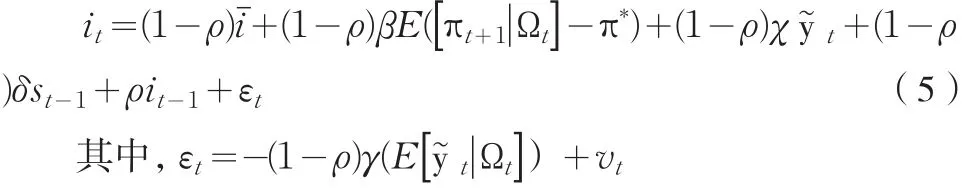
令 a=(1-ρ)，a=(1-ρ)，ϕ=(1-ρ)β ，φ=(1-ρ)χ，γ=(1-ρ)δ，则我们得到考虑资产价格波动的前瞻性泰勒规则模型为：

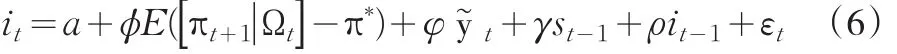
其中，i表示市场利率，E([πt+1|Ωt])表示预期通货膨胀缺口，y͂t表示产出缺口，st-1表示滞后一期资产价格，it-1表示滞后一期市场利率。

2 数据选取与处理

本文选取的样本为我国2000年第一季度到2009年第四季度，共40个样本数据。数据来源于ccer经济金融数据库。变量的数据选取及处理做如下说明：

2.1 名义利率与长期均衡利率

由于我国国债利率尚不能引导市场利率。而同业拆借利率能够较为迅速地反映货币市场上资金的供求状况（谢平、罗雄，2002;卞志村，2006等），所以本文沿用国内研究的普遍做法将银行七日同业拆借利率作为金融市场的基准利率。

长期均衡利率值的主要方法是平均联邦基金利率与平均通货膨胀率之差（Kozicki，1999；clarida，Gali and Gerlter，2000），谢平、罗雄（2002）也认为如果样本期限足够长，可以用样本的平均真实利率来估计长期均衡真实利率。由于近年我国通货膨胀率较高以及选取样本的期限不够长，为了避免出现较大的误差，我们用1992～2009年的长期平均真实利率代表我国长期均衡利率，通过计算可得：长期均衡利率iˉ=2.347。

2.2 潜在GDP与GDP缺口的估计

为了消除通货膨胀的影响，我们将名义季度GDP转化为真实季度GDP(用RGDP表示)，方法为:真实季度GDP=名义季度GDP/当季CPI。我们用线性趋势来估计潜在GDP。由于GDP水平呈现出强烈的季节波动，首先用X11季节调整方法消除时间序列中的季节变动要素，然后通过Hodrick-Prescott（HP）滤波法分解序列的趋势要素，进而得出潜在GDP和GDP缺口。

2.3 目标通货膨胀率与预期通货膨胀率

根据《政府工作报告》和国家信息中心披露的信息，我国目标通货膨胀率应维持在3%～5%之间应该是宏观调控的目标。本文通过Fishier交易方程式法计算目标通货膨胀率，即P=MV*/Y*,其中M代表货币供应量(M2),V*代表均衡货币流通速度，Y*代表潜在产出（陆军、钟丹，2003）。把每年实际的年平均值视为年均衡值，用2000～2009年的年实际流通速度的加权平均值代表这一时期的货币均衡流通速度，用每年货币供给量的加权平均值代表这一时期的货币供给量，再根据上文得出的潜在产出得到目标通货膨胀率π*=3.991。

目前文献中估算预期通货膨胀率的方法有两类:一是直接估计的方式，主要依据Lucas供给曲线所导出的预期修正的菲利普斯曲线。二是间接估计的方式。根据费雪方程式估计隐含的预期通货膨胀率。本文借鉴陆军（2002）的研究，引入菲利普斯—奥肯曲线以估算预期的通胀率。

πt=f(ut)+πt*=πt*+b(ut-u*)——菲利普斯曲线

u=u*-a*y͂t——奥肯法则

其中，u与u*表示实际与自然失业率。y͂t表示产出缺口。将奥肯法则和菲利浦斯曲线结合起来，得到菲利普斯-奥肯曲线:

则预期通货膨胀率

2.4 资产价格

采用上海证券综合指数季度数据来代表资产价格。从图1可以看出从2000年第一季度到2009年第四季度股票市场价格波动是较大的,尤其是在2006～2009年大幅起落。

3 实证分析与结果说明

3.1 ADF平稳性检验

首先，为了避免模型出现伪回归问题，本文将利用Dichey和Fuller（1981）提出的考虑残差项序列的ADF单位根检验法，检验变量的平稳性。因此，运用Eviews5.0分别对各变量进行单位根检验。检验过程中滞后项的确定采用SIC准则，自动选择。具体结果见表1：。

由上表的检验结果可得出，变量本身非平稳序列，但一阶差分后均是平稳的，服从I（1）过程，因此，我们不能用传统的计量分析方法检验它们之间的关系，而应该采用处理非平稳变量的协整分析方法。

图1 上证综合指数季度波动

3.2 Johansen协整检验

通过变量的平稳性检验可以发现所有变量均为一阶单整。当以单位根检验得到变量不全为平稳序列时，须进一步确定VAR模型的滞后期数。通过建立无约束的向量自回归（VAR）模型，根据VAR模型中滞后长度标准检验中的AIC信息规则，可以确定最优滞后期数为2。然后利用Johansen检验判断它们之间是否存在协整关系。检验结果如表2所示。

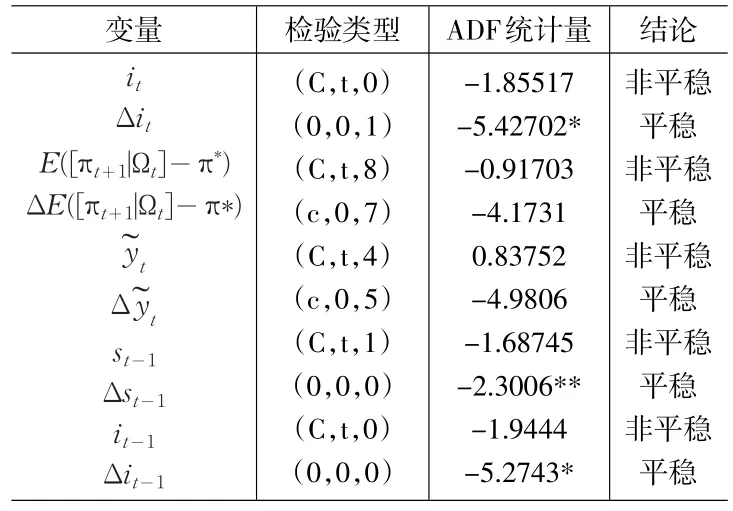
表1 ADF平稳性检验结果

由检验结果可知，在5%的显著水平下，存在一个且仅存在一个协整关系。即表明各变量之间存在长期稳定的均衡关系，且协整方程为

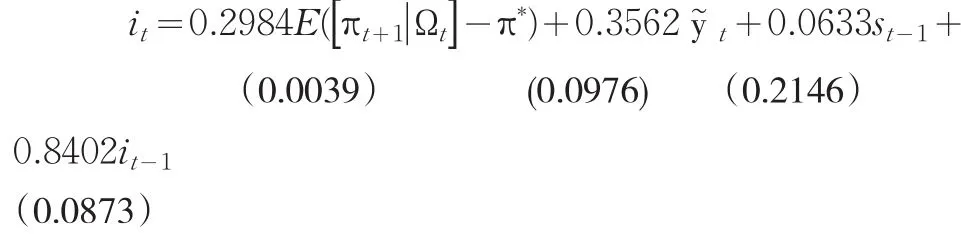
协整检验结果表明市场利率利率、预期通货膨胀缺口、产出缺口、资产价格与滞后一期市场利率之间实存在长期均衡关系。每个估计符号均符号理论要求，考虑资产价格后的前瞻性泰勒规则适合描述我国银行同业拆借利率的长期走势。

表2 Johansen协整关系检验

预期通货膨胀E([πt+1|Ωt]-π*)的反应系数为0.2984，明显小于1。这说明我国货币政策是一种不稳定的货币政策。当经济处于高涨时期，利率上升幅度小于通货膨胀率，结果相当于真实利率下降，从而更进一步刺激投资，加速经济增长，使通货膨胀进一步上升。央行在货币政策执行过程中考虑到了微观主体的预期,但是关注程度小于对预期通胀的程度。

产出缺口y͂t反应系数为0.3262。泰勒(1998)计算的美国在1987～1997年期间产出缺口的利率系数为0.765，英国1992～1997年期间的产出缺口系数为0.47，都高于我国的产出缺口系数。虽然我国产出系数微偏小，但表明我国在这一段时期实行的货币政策已经开始重视产出缺口问题。

利率平滑it-1的系数为0.8402，小于1但相差不大，这表明央行能够根据经济发展变化，对利率进行主动调节的同时采用了利率平滑的调控方式，有利于维护央行信誉，防止对市场造成过度冲击。

资产价格（股票总市值）st-1的系数为0.0633，这表明当资产价格波动对利率的存在正向的影响，但是市场利率反应的幅度远远低于资产价格波动的幅度。

3.3 反应函数估计

我们采用GMM广义矩阵法估计反应函数进一步检验上述结论。工具变量集合包括常量、滞后两阶的名义短期利率、预期通胀缺口、产出缺口、资产价格。

GMM估计的结果表明，中央银行在调整利率水平时对预期通胀缺口、产出缺口、资产价格、利率平滑的反应系数分别为0.0379、0.4025、0.0434、0.9246，与协整检验结果基本一致，印证了我国中央银行货币政策存在明显利率平滑行为、对预期通货膨胀缺口和资产价格反应不足的结论。

然后将考虑资产价格波动的前瞻性泰勒规则与传统泰勒规则估计的目标利率值进行比较。图2中i表示市场利率原值，i_a表示传统泰勒规则对利率模拟值，i_b表示考虑资产价格波动的前瞻性泰勒规则对利率模拟值。表4为描述性统计数据的比较。

从上述比较可以看出，加入资产价格的前瞻性泰勒规则模型比原泰勒规则模型对目标利率的模拟较好，更符合我国市场利率的走势。因此，泰勒规则在我国的运用应当考虑资产价格波动。因此,资产价格应该成为今后中央银行利率调控的重要内生变量。

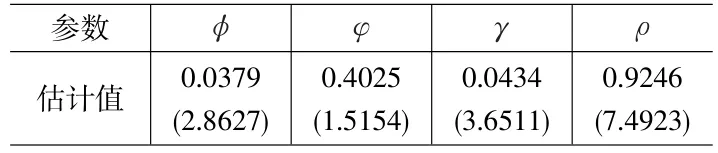
表3 GMM反应函数估计结果

4 研究结论与建议

本文将资产价格引入泰勒规则，并考虑前瞻性通货膨胀预期，构建了中国货币政策利率反应模型。并基于2000～2009年中国宏观经济季度数据，运用协整检验和反应函数估计法对拓展后的泰勒规则模型进行检验和比较。本文得出以下结论：

第一，考虑资产价格波动的前瞻性泰勒规则更适合描述我国市场利率走势。协整检验表明滞后一期资产价格与市场利率、预期通货膨胀缺口、滞后一期市场利率之间存在长期均衡关系。反应函数法与协整检验的结论基本一致。并且通过对比发现，考虑资产价格波动的前瞻性泰勒规则对我国市场利率的模拟更好，泰勒规则在我国的运用应当将资产价格纳入框架，资产价格应该成为今后中央银行利率调控的重要内生变量。

图2 基准模型、扩展模型模拟值与实际值比较

表4 实际利率与基准模型、扩展模型模拟值描述统计比较

第二，利率调整对预期通胀缺口前瞻性不足。从协整检验结果看,我国中央银行货币政策对预期通货膨胀缺口的反应系数为0.2984，反应不足。这会利率上升幅度小于通货膨胀率，结果相当于真实利率下降，从而更进一步刺激投资，加速经济增长，使通货膨胀进一步上升。这说明目前我们的货币政策是一种不稳定的货币政策。货币政策从制定、实施到影响实体经济之间存在时滞问题,认为未来物价有通货膨胀压力时就应该及时调整，因此央行应提高对通货膨胀的前瞻性预期，达到利率对通货膨胀的合理调控。

第三，市场利率对资产价格反应不足。资产价格st-1的系数为0.0633，GMM反应函数估计的系数为0.0434，反应程度均偏小。一方面原因可能是这一期间央行货币政策以稳定物价、保经济增长为主，而对资产价格反应不足，另一方面原因是资产价格的波动不仅受到货币政策的影响，还受到市场参与者对市场的预期、外部经济因素的影响，并且货币政策主要影响的是短期利率，而资产价格主要反映的是人们对长期利率水平的预期。

基于此，我们建议建立通货膨胀监测体系，根据物价水平和人们预期变化对宏观经济影响程度的估计估计做出相应判断，加强货币政策的前瞻性。并且随着我国资本市场不断壮大以及金融衍生产品的日益丰富，金融资产占社会经济总资本的比重日益增大。资产价格如果出现剧烈波动将不可避免地影响货币政策效果，甚至会对宏观经济基本面产生严重冲击。因此，必须通过加强金融监管规范资产市场行为，完善资产价格的货币政策传导机制，提高货币政策有效性。

[1]Taylor,John B.Discretion V ersus Policy Rules in Practice[J].Carnegie-Rochester Conference Serieson Public Policy，1993，39.

[2]Orphanides A.(2001),"Monetary Policy Rules Based on Real-time data American Economic Review，2001，91（4）.

[3]Carida,R.,J.Gali，M.Gentler.Monetary Policy Rules and Macroecnomic Stability[J].Quarterly Journal of Economics，2000，115(1).

[4]Qrphanides,A.Historical Monetary Policy Analysis and the Taylor Rule[J].Journal of Monetary Economics,2003,50(5).

[5]Siklos,P.L.,T.Werner，M.T.BohlAsset Pricesin Taylor rules:Specification,Estimation,and Policy Implications for the ECB[C].Bundesbank Discussion Paper Series1，No.22，2004.

[6]Ball,Laurence.Policy Rules for Open Economies[A].in J.Taylor(ed.)Monetary Policy Rules[M].Chicago:University of Chicago Press,1999.

[7]Svensson,Lars E.O.Open-Economy Inflation Targeting[J].Journal of International Economics,2000,3.

[8]Hans Genberg.Asset Price，Monetary Policy and Macroeconomic Stability[Z].DEWCONOMIST，NO4，2001.